Полное внутреннее отражение в призме
До сих пор мы предполагали, что луч, войдя в призму через одну грань, обязательно выйдет через другую. Но на самом деле бывает и по-другому: дойдя до второй грани, луч может испытать полное внутреннее отражение и вообще не выйти наружу через эту грань! Чтобы лучше разобраться с этим вопросом, решим задачу.
Задача 6.2. При каком наименьшем значении преломляющего угла А стеклянной призмы ВАС (рис. 6.5) луч SM будет претерпевать полное отражение (п = 1,5)? Луч падает из воздуха.
| n = 1,5 | Решение. Как видно из рис. 6.5, луч падает на вторую грань под углом a. В самом деле, a = ÐВАС = ÐNМK как углы со взаимно перпендикулярными сторонами. |
| a= ? | |
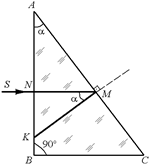 Рис. 6.5
Рис. 6.5
|
Для того чтобы луч испытал в точке М полное внутреннее отражение, необходимо, чтобы выполнялось равенство
 То есть минимальный угол a0, начиная с которого луч будет испытывать полное внутреннее отражение на второй грани, равен 42°.
То есть минимальный угол a0, начиная с которого луч будет испытывать полное внутреннее отражение на второй грани, равен 42°.
Ответ: a » 42°.
СТОП! Решите самостоятельно: А5, А6, В5–В8, С4.
Задача 6.3. Построить ход луча из воздуха сквозь треугольную стеклянную призму (рис. 6.6), преломляющий угол которой 80°, а показатель преломления 1,73. Угол падения луча при входе в призму равен 60°.
| n = 1,73 a = 60° j = 80° |  Рис. 6.6 Рис. 6.6
|
| q= ? |
Решение. 1. Рассмотрим преломление луча в точке А:

2. Для того чтобы найти угол падения a на вторую грань, воспользуемся формулой (6.2):
j = b + a1 Þ a1 = j – b = 80° – 30° = 50°.
3. Выясним, испытает ли луч в точке В полное внутреннее отражение. Предельный угол внутреннего отражения равен:

Значит, наш луч не выйдет наружу, а отразится от грани OK зеркально и упадет на грань LK.
4. Найдем угол падения луча на грань LK. Для этого рассмотрим DBCK: ÐСBK = 90° – 50° = 40°, ÐBKС – это угол при вершине равнобедренного ÐLOK с углом при вершине 80°. Поэтому
 .
.
Найдем ÐBCK. Так как сумма углов в DBCK равна 180°, то
ÐBCK = 180° – ÐBKС – ÐСBK = 180° – 50° – 40° = 90°.
Иными словами, луч перпендикулярен грани LK, поэтому он выходит из призмы через эту грань, не преломляясь.
Ответ: луч преломится на правой грани с углом преломления 30°, полностью отразится от второй грани и выйдет наружу через основание призмы перпендикулярно к этому основанию.
СТОП! Решите самостоятельно: С5–С7, D3.
Задача 6.4. У призмы с преломляющим углом 30° одна грань посеребрена. Луч, падающий на другую грань под углом 45°, после преломления и после отражения от посеребренной грани вернулся назад по прежнему направлению. Чему равен показатель преломления материала призмы?
| a = 45° j = 30° | Решение. 1. Рассмотрим преломление луча в точке А (рис. 6.7):
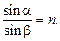 (1) (1)
|
| п = ? |
 Рис. 6.7
Рис. 6.7
|
2. Поскольку, отразившись в точке В, луч пошел обратно по той же траектории, то ÐABN = 90°, тогда угол преломления
b = ÐВAN = ÐLOK = j = 30°
как углы со взаимно перпендикулярными сторонами.
3. Итак, нам известен угол падения a = 45° и угол преломления b = 30° в точке А. Подставим эти значения в (1) и найдем п:

Ответ: 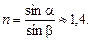
СТОП! Решите самостоятельно: В9, С8.
Дата добавления: 2016-04-11; просмотров: 8490;
