Чему равна ЭДС самоиндукции?
Согласно закону Фарадея ℰis = – 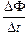 . Если Ф = LI, то ℰis = = –
. Если Ф = LI, то ℰis = = – 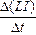 . При условии, что индуктивность контура в процессе изменения тока не меняется (т.е. не меняются геометрические размеры контура и магнитные свойства среды), то
. При условии, что индуктивность контура в процессе изменения тока не меняется (т.е. не меняются геометрические размеры контура и магнитные свойства среды), то
ℰis = – 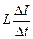 . (13.2)
. (13.2)
Из этой формулы видно, что если индуктивность катушки L достаточно велика, а время изменения тока мало, то величина ℰis может достигнуть большой величины и превысить ЭДС источника тока при размыкании цепи. Именно этот эффект мы наблюдали в опыте 1.
Из формулы (13.2) можно выразить L:
L = – ℰis/(DI/Dt),
т.е. индуктивность имеет еще один физический смысл: она численно равна ЭДС самоиндукции при скорости изменения тока через контур 1 А в 1 с.
Читатель: Но тогда получится, что размерность индуктивности
| [L] = | [ℰ] | = 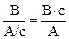 . А раньше мы получили, что [L] = . А раньше мы получили, что [L] =
|
| [I]×[t] |
= Вб/А = Гн.
Автор: Вспомним, что ℰi = – 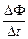 , отсюда [Ф] = [ℰ][t], т.е. Вб = В×с. Так что
, отсюда [Ф] = [ℰ][t], т.е. Вб = В×с. Так что 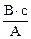 и
и 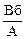 – это одно и то же:
– это одно и то же:
[L] = Гн = 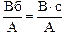 .
.
СТОП! Решите самостоятельно: А3, А4, В3–В5, С1, С2.
Задача 13.2. Какова индуктивность катушки с железным сердечником, если за время Dt = 0,50 с ток в цепи изменился от I1 = = 10,0 А до I2 = 5,0 А, а возникшая при этом ЭДС самоиндукции по модулю равна |ℰis| = 25 В?
| Dt = 0,50 с I1 = 10,0 А I2 = 5,0 А |ℰis| = 25 В | Решение. Воспользуемся формулой (13.2). Из нее следует, что
|ℰis| = 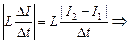 L = ℰis
L = ℰis 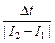 = = 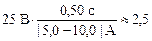 Гн. Гн.
|
| L = ? | |
Ответ: L = ℰis 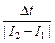 » 2,5 Гн.
» 2,5 Гн.
СТОП! Решите самостоятельно: А5, А6, В6.
Читатель: А какой смысл имеет знак минус в формуле (13.2)?
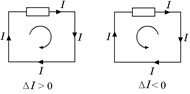 Рис. 13.6
Рис. 13.6
|
Автор: Рассмотрим какой-либо проводящий контур, по которому течет ток. Выберем направление обхода контура – по или против часовой стрелки (рис. 13.6). Вспомним: если направление тока совпадает с выбранным направлением обхода, то сила тока считается положительной, а если нет – отрицательной.
Изменение тока DI = Iкон – Iнач – также величина алгебраическая (отрицательная или положительная). ЭДС самоиндукции – это работа, совершаемая вихревым полем при перемещении единичного положительного заряда по контуру вдоль направления обхода контура. Если напряженность вихревого поля направлена вдоль направления обхода контура, то эта работа положительна, а если против – отрицательна. Таким образом, знак минус в формуле (13.2) показывает, что величины DI и ℰis всегда имеют разные знаки.
Покажем это на примерах (рис. 13.7):
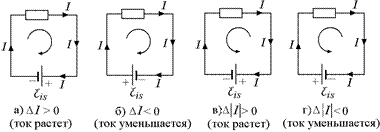
Рис. 13.7
а) I > 0 и DI > 0, значит, ℰis < 0, т.е. ЭДС самоиндукции «включена» навстречу направлению обхода;
б) I > 0 и DI < 0, значит, ℰis > 0, т.е. ЭДС самоиндукции «включена» вдоль направления обхода;
в) I < 0, а D|I| > 0, т.е. модуль тока возрастает, а сам ток становится все «более отрицательным». Значит, DI < 0, тогда ℰis > 0, т.е. ЭДС самоиндукции «включена» вдоль направления обхода;
г) I < 0, а D|I| < 0, т.е. модуль тока уменьшается, а сам ток становится все «менее отрицательным». Значит, DI > 0, тогда ℰis < 0, т.е. ЭДС самоиндукции «включена» навстречу направлению обхода.
В задачах, по возможности, следует выбирать такое направление обхода, чтобы ток был положительным.
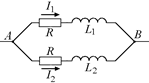
Задача 13.3. В цепи на рис. 13.8, а L1 = 0,02 Гн и L2 = 0,005 Гн. В некоторый момент ток I1 = 0,1 А и возрастает со скоростью 10 А/с, а ток I2 = 0,2 А и возрастает со скоростью 20 А/с. Найти сопротивление R.
  а б
Рис. 13.8
Решение. Так как оба тока возрастают, то в обеих катушках возникают ЭДС самоиндукции ℰis1
а б
Рис. 13.8
Решение. Так как оба тока возрастают, то в обеих катушках возникают ЭДС самоиндукции ℰis1
| |
| L1 = 0,02 Гн L2 = 0,005 Гн I1 = 0,1 А I2 = 0,2 А DI1/Dt = 10 А/с DI2/Dt = 20 А/с | |
| R = ? | |
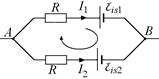
и ℰis2, включенные навстречу токам I1 и I2 (рис. 13.8, б), где
|ℰis1| = 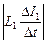 ; |ℰis2| =
; |ℰis2| = 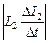 .
.
Выберем направление обхода по часовой стрелке (см. рис. 13.8,б) и применим второе правило Кирхгофа
–|ℰis1| + |ℰis2| = I1R – I2R ,
R = |ℰis2| – |ℰis1| / (I1 – I2) = 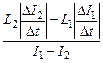 =
=
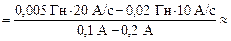 1 Ом.
1 Ом.
Ответ: R = 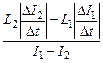 » 1 Ом.
» 1 Ом.
СТОП! Решите самостоятельно: В7, В8, С3.
Задача 13.4. Катушка сопротивлением R = 20 Ом и индуктивностью L = 0,010 Гн находится в переменном магнитном поле. Когда создаваемый этим полем магнитный поток увеличился на DФ = = 0,001 Вб, ток в катушке возрос на DI = 0,050 А. Какой заряд прошел за это время по катушке?
| R = 20 Ом L = 0,010 Гн DФ = 0,0010 Вб DI = 0,050 А | Решение. Внешнее переменное магнитное поле создало в катушке ЭДС индукции |ℰi| = 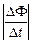 . Благодаря этой ЭДС в катушке стал увеличиваться ток, а из-за этого в катушке возникла ЭДС самоин- . Благодаря этой ЭДС в катушке стал увеличиваться ток, а из-за этого в катушке возникла ЭДС самоин-
|
| q = ? | |
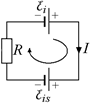 Рис. 13.9
Рис. 13.9
|
дукции |ℰis| = 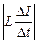 . Причем ℰis «включилась» навстречу ℰi, так как ток в цепи возрастал (рис. 13.9).
. Причем ℰis «включилась» навстречу ℰi, так как ток в цепи возрастал (рис. 13.9).
Возьмем направление обхода контура по часовой стрелке. Тогда согласно второму правилу Кирхгофа получим:
|ℰi| – |ℰis| = IR ,
I = (|ℰi| – |ℰis|)/R = 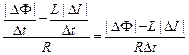 .
.
Заряд q, прошедший по катушке за время Dt, равна
q = IDt = 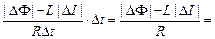
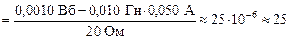 мкКл.
мкКл.
Ответ: 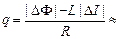 25 мкКл.
25 мкКл.
СТОП! Решите самостоятельно: В9, В10, С4.
Задача 13.5. Катушка с индуктивностью L и электрическим сопротивлением R подключена через ключ к источнику тока с ЭДС ℰ. В момент t = 0 ключ замыкают. Как изменяется со временем сила тока I в цепи сразу же после замыкания ключа? Через длительное время после замыкания? Оцените характерное время t возрастания тока в такой цепи. Внутренним сопротивлением источника тока можно пренебречь.
| ℰ R L | Решение. ЭДС самоиндукции ℰis = – 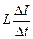 , поэтому согласно закону Ома для полной цепи IR = ℰ + ℰis = ℰ – , поэтому согласно закону Ома для полной цепи IR = ℰ + ℰis = ℰ – 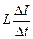 (рис. 13.10, а). Перепишем это соотношение в виде (рис. 13.10, а). Перепишем это соотношение в виде
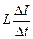 = ℰ – IR. (1) = ℰ – IR. (1)
|
| I(t) = ? t = ? | |
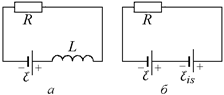 Рис. 13.10
Рис. 13.10
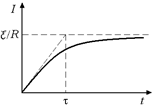 Рис. 13.11
Рис. 13.11
|
Сразу же после замыкания ключа I = 0, поэтому можно считать 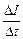 » ℰ/L, т.е. ток возрастает с постоянной скоростью (I = (ℰ/L)t;рис. 13.11).
» ℰ/L, т.е. ток возрастает с постоянной скоростью (I = (ℰ/L)t;рис. 13.11).
При увеличении тока правая часть в уравнении (1) уменьшается, следовательно, уменьшается и скорость возрастания тока. Через достаточно длительное время (о том, каким оно должна быть, – чуть ниже) правая часть уравнения (1) становится пренебрежимо малой. Это означает, что ток стремится к постоянной величине I = ℰ/R (см. рис. 13.11).
«Характерное» время t для рассматриваемой системы можно определить, оценив, когда слагаемое IR станет сравнимо по величине с ℰ. Воспользовавшись для оценки зависимостью I = (ℰ/L)t,получаем (ℰ/L)tR » ℰ Þ t » L/R.
Точное значение тока в момент времени t можно найти, решив дифференциальное уравнение, к которому сводится уравнение (1):
LI¢ = ℰ – IR (2)
при начальном условии I(0) = 0. «Угадаем» решение:
I(t) = (ℰ/R) 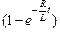 .
.
Убедимся, что это действительно решение. В самом деле:
1) начальные условия выполняются:
I(0) = (ℰ/R) 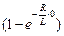 = (ℰ/R)(1 – 1) = 0;
= (ℰ/R)(1 – 1) = 0;
2) левая часть уравнения (2) тождественна правой:
л.ч. LI¢ = L[(ℰ/R) 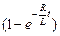 ]¢ = (Lℰ/R)
]¢ = (Lℰ/R) 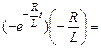 ℰ
ℰ 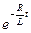 ;
;
п.ч. ℰ – IR = ℰ – (ℰ/R) 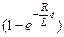 R = ℰ
R = ℰ 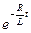 .
.
Поскольку в теории дифференциальных уравнений доказано, что уравнения данного типа имеют единственное решение, то других решений нет.
Ответ: t » L/R, I(t) = (ℰ/R) 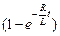 .
.
СТОП! Решите самостоятельно: С5, D2.
Дата добавления: 2016-04-11; просмотров: 4053;
