Как определить электрохимический эквивалент?

Читатель: По-моему, это чисто экспериментальная задача.

Автор: Да, если… нам не удастся вывести закон Фарадея чисто теоретически! Давайте попробуем.

Масса т выделившегося вещества равна произведению массы одного иона т_i на число ионов N_i, осевших на электроде за время Dt:

т = m_iN_i. (1)

Масса иона, как мы уже знаем, равна

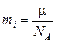, (2)

где m – молярная (или атомная) масса вещества, a N_A – по­стоянная Авогадро, т. е. число ионов в одном моле. Число ионов, осевших на электроде,

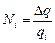, (3)

где Dq = IDt – заряд, протекший через раствор электролита за время Dt, q_i – заряд иона, который равен произведению эле­ментарного заряда е на валентность п атома (или группы ато­мов), из которого образовался ион: q_i = en.

При диссоциации молекул, состоящих из одновалентных ато­мов (п = 1), возникают однозарядные ионы. Например, при дис­социации молекулы бромида калия KВr возникают ионы K⁺ и Вr^–, а при диссоциации молекулы медного купороса CuSO₄ полу­чаются два двухзарядных иона Сu²⁺ и , так как атом меди и кислотный остаток в данном соединении двухвалентны (п = 2). Подставляя в формулу (1) выражения (2) и (3) и учитывая, что Dq = IDt и q_i = en, получим

.

Итак,

. (22.3)

Сравнивая (22.3) с (22.1), нетрудно заметить, что

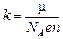. (22.4)

Поскольку 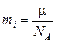– масса иона, а еп = q_i – заряд иона, то выражение для k примет вид:

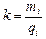, (22.5)

т.е. величина k – это отношение массы иона к его заряду.

Постоянная Фарадея

Произведение элементарного заряда (заряда электрона) е на постоянную Авогадро N_А носит название постоянной Фарадея: F = eN_A. Введя постоянную Фарадея в формулу (22.3), для массы вещества, выделившегося при электролизе наэлектроде, получим:

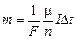. (22.6)

Согласно этой формуле постоянная Фарадея F численно равна заряду, который надо пропустить через раствор элект­ролита, чтобы выделить на электроде один моль одновалент­ного вещества. Постоянная Фарадея, найденная из опыта, равна F = 9,65×10⁴ Кл/моль. Для выделения на электроде одного моля п-валентного вещества через раствор электролита необходимо пропустить заряд, численно равный произведе­нию nF.

Сравнивая формулы (22.6) и (22.1), можно получить еще одну формулу для k:

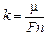. (22.7)