Электрического тока. Согласно формуле (15.6) мощность электрического тока равна:
Согласно формуле (15.6) мощность электрического тока равна:
P = UI. (1)
Согласно закону Ома:
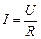 . (2)
. (2)
Подставим значение I из (2) в (1) и получим:
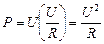 .
.
Мы получили еще одну формулу для расчета мощности тока:
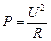 . (15.11)
. (15.11)
Теперь выразим из формулы (2) напряжение через ток и сопротивление:
U = IR. (3)
Подставим значение U из (3) в (1) и получим:
P = (IR) × I = I2R.
Итак:
P = I2R. (15.12)
СТОП! Решите самостоятельно: С1, С2.
Задача 15.1. Какую мощность будет потреблять 25-ваттная лампочка, рассчитанная на напряжение U1 = 120 В, если ее включить в сеть с напряжением U2 = 220 В?
| Р1 = 25 Вт U1 = 120 В U2 = 220 В | Решение. Пусть R – сопротивление лампы, тогда согласно формуле (15.10)
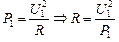 .
Находим искомую мощность .
Находим искомую мощность
|
| Р2 = ? | |
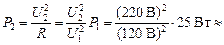 84 Вт.
84 Вт.
Ответ: 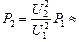 84 Вт.
84 Вт.
СТОП! Решите самостоятельно: А1–А5, В2, В3, С3.
Задача 15.2. Электропечь должна давать количество теплоты Q = 0,10 МДж за время t = 10 мин. Какова должна быть длина нихромовой проволоки сечения S = 0,50 мм2, если печь предназначается для сети с напряжением U = 36 В? Удельное сопротивление нихрома r = 1,2 мкОм×м.
| Q = 0,10 МДж = 1,0×105 Дж t = 10 мин = 6,0×102 с S = 0,50 мм2 = 0,50×10–6 м2 U = 36 В r = 1,2 мкОм×м = 1,2×10–6 Ом×м | Решение. По формуле (15.9)
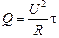 ,
где ,
где 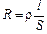 – сопротивление проволоки. Тогда – сопротивление проволоки. Тогда
|
| l = ? |
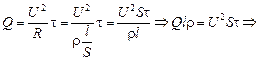
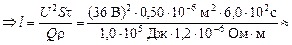 3,2 м.
3,2 м.
Ответ: 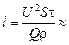 3,2 м.
3,2 м.
СТОП! Решите самостоятельно: А6, В4, В5, С4.
Полезная мощность
Задача 15.3. Источник тока с ЭДС õ и внутренним сопротивлением r подключен к нагрузке сопротивлением R. Определить полезную мощность источника тока – мощность, выделенную на нагрузке. Построить график зависимости полезной мощности от сопротивления нагрузки Р = Р(R).
| õ r R | Решение. Согласно закону Ома для замкнутой цепи ток I = õ/(R + r). Из закона Джоуля–Ленца следует, что мощность, выделяемая на нагрузке, Р = I2R (формула (15.12)). Тогда P = I2R = [õ/(R + r)]2×R = õ2R/(R + r)2. |
| P(R) = ? | |
Итак, получаем ответ:
Р = [õ2/(R + r)2]×R. (15.12)
Построим график Р = Р(R). Если R = 0, то Р = [õ2 /(0 + r)2] ×0 = 0. Если R ® ¥, то Р = 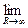 [õ2/(R + r)2] ×R =
[õ2/(R + r)2] ×R = 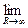 [õ2/R]= 0.
[õ2/R]= 0.
При малых R (R << r) функция Р(R) линейно растет с ростом R: Р » (õ2/r2)×R. При больших R (R >> r) функция Р(R) убывает по закону Р » õ2/R. Значит, при каком-то R функция Р(R) должен иметь максимум. Вычислим производную Р¢(R) и приравняем ее к нулю. Для этого воспользуемся формулой, известной нам из курса математики: 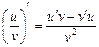 . Получим
. Получим
Р¢(R) = [õ2R /(R + r)2]¢ = õ2 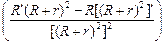 =
=
= 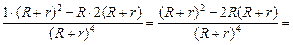
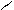
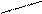
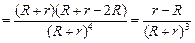 .
.
Приравнивая Р¢(R) к нулю, получим
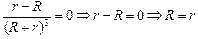 .
.
Значит, при R = r функция Р(R) = õ2R/(R + r)2 достигает максимума, и ее значение при этом равно
Рmax = [õ2r/(r + r)2] = õ2r/4r2 = õ2/4r.
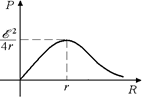 Рис. 15.1
Рис. 15.1
|
Итак, запомним: полезная мощность достигает своего максимального значения, если сопротивление нагрузки R равно внутреннему сопротивлению источника тока; при этом максимальное значение полезной мощности равно
Рmax = õ2/4r. (15.13)
График P(R) показан на рис. 15.1.
СТОП! Решите самостоятельно: А9, А10, В6, В7.
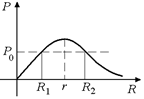 Рис. 15.2
Рис. 15.2
|
Автор: Как Вы считаете, может ли один и тот же источник на разных нагрузках давать одинаковую мощность?
Читатель: Судя по рис. 15.1, наверное может: одной и той же мощность Р0 соответствуют два сопротивления нагрузки R1 и R2 (рис. 15.2).
Автор: Совершенно верно!
Задача 15.4. К источнику ЭДС подключаются поочередно резисторы с сопротивлениями R1 и R2. В обоих случаях на резисторах выделяется одинаковая мощность. Определите внутреннее сопротивление r источника.
| R1 R2 P(R1) = P(R2) | Решение. Обозначим ЭДС источника через õ. Резисторы с сопротивлениями R1 и R2 потребляет соответственно мощности Р1 = [õ2/(R1 + r)2]×R1 и Р2 = [õ2/(R2 + r)2]×R2. Тогда |
| r = ? | |

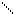 Р1 = Р2 Þ õ2R1/(R1 + r)2 = õ2R2/(R2 + r)2 Þ
Р1 = Р2 Þ õ2R1/(R1 + r)2 = õ2R2/(R2 + r)2 Þ
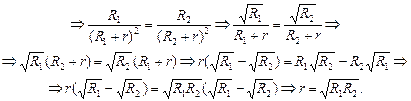
Итак, запомним ответ:
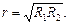 (15.14)
(15.14)
СТОП! Решите самостоятельно: А11, В8–В10, С5.
Полезная, «бесполезная»
И полная мощности
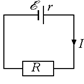 Рис. 15.3
Рис. 15.3
|
Пусть имеется электрическая цепь, показанная на рис. 15.3, где õ – ЭДС, r – внутреннее сопротивление, а R – сопротивление нагрузки. Тогда сила тока в цепи I = õ/(R + r).
Полезной мощностью называется мощность, выделяемая на нагрузке: P = I2R = [õ/(R + r)]2×R – это как раз та мощность, которую получит потребитель тока (лампочка, телевизор и т.д.).
В то же время ток проходит и через источник тока, значит, на нем тоже выделяется мощность, которую условно можно назвать «бесполезной»:
Pб = I2r = [õ/(R + r)]2×r. (15.15)
Полная мощность в цепи равна сумме полезной и «бесполезной» мощностей:
Р0 = Р + Рб = I2R + I2r = I2(R + r) =
= [õ/(R + r)]2(R + r) = õ2/(R + r).
Запомним:
Р0 = õ2/(R + r). (15.16)
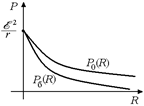 Рис. 15.4
Рис. 15.4
|
Графики зависимости Pб(R) и P0(R) показаны на рис. 15.4. Как видно из рисунка, при R = 0 (короткое замыкание) полная мощность равна «бесполезной» мощности и равна õ2/r.
Заметим также, что полная мощность, выделяемая в цепи, равна мощности сторонних сил, так как вся работа, совершаемая сторонними силами внутри источника тока, расходуется на работу, совершаемую электрическим током в источнике и в сопротивлении нагрузки:
Астор = Р0t Þ Р0 = Астор/t = õq/t,
где q – заряд, переносимый через источник тока за время t. А поскольку q/t = I, то получим
Р0 = õI. (15.17)
Тогда, поскольку Р0 = Р + Рб, получим
Р= Р0 – Рб = õI – I2r.
Запомним, что полезная мощность определяется также формулой
Р = õI – I2r, (15.18)
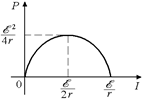 Рис. 15.5
Рис. 15.5
|
которая показывает зависимость полезной мощности от тока. График этой зависимости показан на рис. 15.5. Из графика видно, что полезная мощность достигает максимума при токе I = õ/2r. Величина мощности при этом Рmax = õ2/4r, что полностью согласуется с формулой (15.13).
Читатель: А почему при I = õ/r полезная мощность равна нулю?
Автор: Потому что это – ток короткого замыкания! То есть ситуация, при которой сопротивление нагрузки равно нулю (R = 0):
I = õ/(r + 0) = õ/r.
Ясно, что если R = 0, то
Р = I2r= I2×0 = 0.
СТОП! Решите самостоятельно: А7, А8, А12, В12–В14, С6, С9.
КПД источника тока
Коэффициентом полезного действия (КПД) источника тока называется отношение полезной мощности к полной мощности:
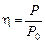 . (15.19)
. (15.19)
Задача 15.5. Найти КПД схемы, в которую включен элемент с ЭДС õ и внутренним сопротивлением r, если ток в цепи равен I. Выразить КПД: черезõ, r и I; через сопротивление внешней цепи R и внутреннее сопротивление элемента r; через õ и напряжение на его зажимах U.
| õ I r R U | Решение. Начнем с последнего вопроса. Вспомним, что напряжение на нагрузке R – это работа по перемещению единичного положительного заряда через это сопротивление, а значит, A = Uq = UIt – это полезная работа. Тогда полезная мощность Р = А/t = UI, а полная мощность согласно формуле (15.17) Р0 = õI. Теперь найдем искомый КПД:
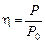 = UI/õI = U/õ. = UI/õI = U/õ.
|
| h = ? | |
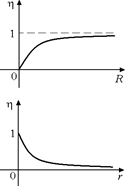 Рис. 15.5
Рис. 15.5
|
Итак, запомним:
h = U/õ. (15.20)
С другой стороны, U = IR = [õ/(R + r)]R. Подставив это выражение в (15.20), получим
| h = | [õ/(R + r)]R | = 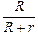 . .
|
| õ |
Запомним:
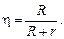 (15.21)
(15.21)
И, наконец, вспомним еще одну формулу: U = õ – Ir, тогда
h = (õ – Ir)/ õ. (15.22)
Графики зависимостей КПД от R и r показаны на рис. 15.6.
СТОП! Решите самостоятельно: А13, А16, В15–В18.
Дата добавления: 2016-04-11; просмотров: 1209;
