РАБОТА И МОЩНОСТЬ ТОКА

Мы уже выяснили, что внутри проводника, по которому течет электрический ток, существует электрическое поле. Под действием сил этого поля электроны упорядоченно движутся в определенном направлении, при этом силы электрического поля совершают над электронами механическую работу.

Попробуем теоретически вычислить, какую работу совершает электрическое поле за время t, если сила тока в проводнике I, а напряжение на его концах U.

Электрическое напряжение равно отношению работы, совершаемой силами электрического поля А к величине заряда q, переносимого через проводник: U = A/q. Отсюда легко по­лучить выражение для работы сил электрического поля в проводнике:

А = Uq. (15.1)

Заметим, что для краткости эту работу называют работой электрического тока или просто работой тока.

Сила тока в проводнике равна: I = q/t, где q – заряд, переносимый через поперечное сечение проводника за время t. Отсюда получаем выражение для заряда q:

q = It. (15.2)

Подставим значение заряда q из (15.2) в (15.1), получим:

А = Uq = U×(It).

Итак:

А = UIt. (15.3)

Мы получили формулу для расчета работы электрического тока.

Читатель: А как быть с размерностью работы? Она ведь измеряется в джоулях, а по формуле (15.3) получается что-то совсем другое...

Автор: Давайте разберемся. Действительно, с одной стороны, едини­цей измерения работы является джоуль: [A] = Дж. А с другой стороны, как Вы правильно заметили, размерность работы из формулы (15.3) получается следующей:

[A] = [U]×[I]×[t] = B × A × c.

В этом нет противоречия. Дело в том, что B × A × c – это и есть джоуль! Действительно: 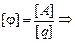В = Дж/Кл, а [q] = [I]×[t] Þ Кл = А×с, тогда B×A×c = (Дж/Кл) ∙ Кл = Дж. Итак:

Дж = В ∙А∙ с. (15.4)

Соотношение (15.4) мы будем использовать при проверке размерностей результатов вычислений в задачах.

Читатель: У меня еще вопрос. Если я правильно понял, для того чтобы совершить работу, нужно затратить энергию. За счет какой же энергии электрический ток совершает работу?

Автор: За счет той самой энергии, которую вырабатывают электростанции, преобразующие в электрическую энергию другие виды энергии. На гидроэлектростанции (ГЭС) в электрическую энергию преобразуется энер­гия падающей воды. На тепловой электростанции (ТЭС) в электрическую энергию преобразуется энергия сжигаемого топлива. На атомной электро­станции (АЭС) в электрическую преобразуется атомная энергия, выделя­ющаяся при делении атомов урана или плутония и т.д. При использовании в качестве источников тока батареек или аккуму­ляторов в электрическую энергию преобразуется химическая энергия.

Читатель: Понятно. Но произведенная током работа должна на что-то «тратиться». То есть опять превращаться в какую-нибудь энергию. На что же идет работа электрического тока?

Автор: В основном эта работа распределяется по двум каналам: 1) на нагревание проводников, например, в электрическом чайнике или в лампе накаливания; 2) на совершение механической работы – главным образом, в электродвигателях.

Мощность тока

Как вы знаете, мощность – это физическая величина, численно рав­ная работе, совершенной в единицу времени. Если за время t была совершена работа А, то мощность Р равна:

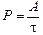. (15.5)

Подставив в формулу (15.5) значение А из формулы (15.3), получим:

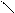
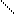
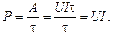
Итак:

Р = UI. (15.6)

Разберемся с размерностью мощности. Мощность, как Вы знаете, измеряется в ваттах (Вт): Вт = Дж/с. С другой стороны, согласно фор­муле (15.6): [P] = [U]×[I] = В×А. Следовательно, справедливо соотношение:

Вт = В×А. (15.7)

Это соотношение пригодится нам при решении задач.

Наряду с ваттом используются следующие единицы измерения мощности:

F 1 киловатт (кВт) = 1000 Вт,

F 1 мегаватт (МВт) = 1 000 000 Вт,

F 1 гигаватт (ГВт) = 1 000 000 000 Вт.

Закон Джоуля–Ленца[1]

Джоуль и Ленц независимо друг от друга экспериментально устано­вили следующий закон. Пусть через проводник сопротивлением R в течение времени t протекает ток, сила тока равна I. Тогда в про­воднике за это время выделяется количество теплоты:

Q = I²Rt. (15.9)

Давайте попробуем вывести формулу (15.9) чисто теоретически.

Если ток течет через неподвижный проводник, то никакой механической работы проводник, понятно, не совершает, а значит, работа электри­ческого тока целиком идет на увеличение внутренней энергии проводника, то есть переходит в тепло. Пусть на концах нашего проводника поддерживается напряжение U, тогда согласно формуле (15.3) работа тока равна:

А = Q = IUt. (1)

Для нашего проводника справедлив закон Ома: 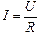, отсюда

U = IR. (2)

Подставим это значение напряжения из (2) в (1) и получим:

Q = IUt = I× (IR)×t = I²Rt.

Формула Джоуля–Ленца доказана.

Рассмотрим другую форму записи закона Джоуля–Ленца. Согласно формуле (15.9):

Q = I²Rt. (3)

Согласно закону Ома:

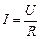. (4)

Подставим значение I из (4) в (3) и получим:

.

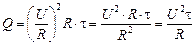Итак:

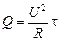. (15.10)