И напряжение на нагрузке
| Автор: Как Вы считаете, что покажут идеальные вольтметры V1 и V2 (рис. 13.11)? То есть каково напряжение на источнике и каково напряжение на нагрузке? Читатель: По-моему, оба вольтметра покажут одно и то же – разность потенциалов точек а и b: jа – jb = IR = [õ/(R + r)]R. |  Рис. 13.11
Рис. 13.11
|
Автор: Совершенно верно. Замечу лишь, что это же выражение можно получить, применив закон Ома для участка цепи, содержащего ЭДС, к участку цепи ba:
jа = jb + õ – Ir Þ jа – jb = õ – Ir = õ –[õ/(R + r)]r =
= [õ (R + r) – õr] / (R + r) = õR/(R + r).
Итак, запомним: напряжение на нагрузке равно напряжению на источнике:
U = õ – Ir = õR/(R + r). (13.5)
Задача 13.5. Каково напряжение на полюсах источника с ЭДС, равной õ, когда сопротивление внешней части цепи равно внутреннему сопротивлению источника?
| õ R = r | Решение. Согласно формуле (13.5) U = õR/(R + r) = õR/(R + R) = õR/2R = õ/2. Ответ: U = õ/2. |
| U = ? | |
СТОП! Решите самостоятельно: А3– А5, В4, В9, В10, С5.
Задача 13.6. Батарея с ЭДС õ = 6,0 В и внутренним сопротивлением r = 1,4 Ом питает внешнюю цепь, состоящую из двух параллельно соединенных резисторов с сопротивлениями R1 = 2,0 Ом и R2 = 8,0 Ом (рис. 13.12). Найти разность потенциалов U на полюсах батареи и силы I1 и I2 токов, текущих через резисторы.
| õ = 6,0 В r = 1,4 Ом R1 = 2,0 Ом R2 = 8,0 Ом | Решение. Общее сопротивление нагрузки
 Ом.
Тогда сила тока в неразветвленной части цепи равна
I = õ/(R + r) = Ом.
Тогда сила тока в неразветвленной части цепи равна
I = õ/(R + r) = 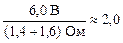 А. А.
|
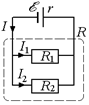 Рис. 13.12
Рис. 13.12
|
| U = ? I1 = ? I2 = ? | ||
Отсюда U = IR = 2,0 А × 1,6 Ом » 3,2 В. Поскольку сопротивления R1 и R2 соединены параллельно, то I1R1 = I2R2 и I = I1 + I2, отсюда
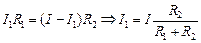 и
и 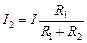 .
.
Подставим численные значения
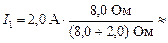 1,6 А;
1,6 А; 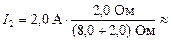 0,40 А.
0,40 А.
Ответ: U » 3,2 В; I1 » 1,6 А; I2 » 0,40 А.
СТОП! Решите самостоятельно: В11, В12, В15, С6–С8.
Задача 13.7. Два вольтметра, соединенные между собой последовательно, при подключении к зажимам ненагруженной батареи показывают: один U1, другой U2. При включении только первого вольтметра он показывает соответственно 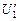 . Определить по этим показаниям ЭДС батареи.
. Определить по этим показаниям ЭДС батареи.
U1
U2
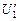
| а) 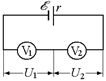 б) б) 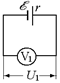 Рис. 13.13 Рис. 13.13
|
| õ = ? |
Решение. В случае, показанном на рис. 13.13,а, напряжение на зажимах источника равно
U1 + U2 = õ – Iar. (1)
Если R1 – сопротивление вольтметра U1, то
Ia = U1/R1. (2)
В случае, показанном на рис. 13.13,б:
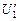 = õ – Iбr, (3)
= õ – Iбr, (3)
Iб = 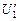 /R1. (4)
/R1. (4)
Подставим (2) в (1), а (4) в (3) и получим
U1 + U2 = õ – U1 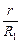 , ,
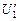 = õ– = õ– 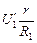
| 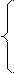 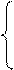 U1 U1 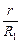 = õ – U1 – U2, (5) = õ – U1 – U2, (5)
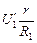 = õ – = õ – 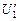 . (6) . (6)
|
Разделив (5) на (6), получим
U1/ 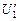 = (õ – U1 – U2)/( õ –
= (õ – U1 – U2)/( õ – 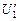 ) Þ U1(õ –
) Þ U1(õ – 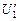 ) =
) = 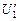 (õ – U1 – U2) Þ
(õ – U1 – U2) Þ
 õ (U1 –
õ (U1 – 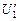 ) = U1
) = U1 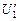 –
– 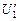 U1 –
U1 – 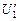 U2 Þ õ =
U2 Þ õ = 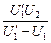 .
.
Ответ: õ = 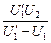 .
.
СТОП! Решите самостоятельно: В17–В19, С12, С14.
Задача 13.8.В схему (рис. 13.14) включены два микроамперметра и два одинаковых вольтметра. Показания микроамперметров I1 = 100 мкА, I2 = 99 мкА, показание вольтметра U1 = 10 В. Найти показание вольтметра U2. Сопротивлением проводов пренебречь.
| I1 = 100 мкА I2 = 99 мкА U1 = 10 В | Рис. 13.14 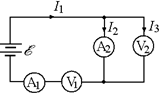
|
| U2 = ? | |
Решение. Из рисунка видно, что I1 = I2 + I3 Þ I3 = I1 – I2. Пусть сопротивление каждого вольтметра равно R, тогда
U1 = I1R и U2 = (I1 – I2)R.
Разделив второе уравнение на первое, получим
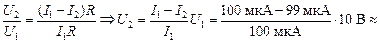
» 0,1 В.
Ответ: 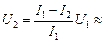 0,1 В.
0,1 В.
СТОП! Решите самостоятельно: В21, С18, С20.
Задача 13.9. Два источника соединены, как показано на рис. 13.15. Определить разность потенциалов между точками А и В.
| õ1 r1 õ2 r2 | 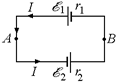 Рис. 13.15
Рис. 13.15
| Решение. Ток в цепи пойдет против часовой стрелки. Согласно формуле (13.3), поскольку оба источника включены в одном направлении, а внешнее сопротивление отсутствует, сила тока равна I = (õ1 + õ2) / (r1 + r2). |
| jА – jВ = ? | ||
Теперь применим закон Ома для участка цепи, содержащего ЭДС, для нижнего участка и получим:
jВ = jА + õ2 – Ir2 Þ jА – jВ = –õ2 + Ir2 =
= –õ2 + [(õ1 + õ2)/(r1 + r2)] r2 = [–õ2(r1 + r2) + r2(õ1 + õ2)]/(r1 + r2) =
= (–õ2r1 + õ1r2)/(r1 + r2) = (õ1r2 – õ2r1)/(r1 + r2).
Ответ:
jА – jВ = (õ1r2 – õ2r1)/(r1 + r2). (13.6)
Заметим, что jА – jВ может быть как положительной, так и отрицательной величиной. А если, например, õ1 = õ2 и r1 = r2, то jА – jВ = 0, т.е. jА = jВ.
СТОП! Решите самостоятельно: В22, В23, В25, В26, С24, С25.
Задача 13.10. Два источника ЭДС соединены, как показано на рис. 13.16 (õ1 > õ2). Определить разность потенциалов между точками А и В.
| õ1 r1 õ2 r2 | Решение. Так как õ1 > õ2, то ток будет идти против часовой стрелки: I = (õ1 – õ2) / (r1 + r2). Применим закон Ома для участка цепи, содержащего ЭДС, для верхнего участка и получим: | 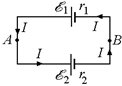 Рис. 13.16
Рис. 13.16
|
| jА – jВ = ? | ||
jА = jВ + õ1 – I1r1 Þ jА – jВ = õ1 – Ir1 =
= õ1 – [(õ1 – õ2)/(r1 + r2)] r1 = [õ1(r1 + r2) – r1(õ1 – õ2)]/(r1 + r2) =
= (õ1r2 + õ2r1)/(r1 + r2) > 0.
Ответ: jА – jВ = (õ1r2 + õℰ2r1)/(r1 + r2).
Заметим, что в данном случае при любых соотношениях между õ1, õ2, r1 и r2 jА > jВ.
СТОП! Решите самостоятельно: В28, С27, С28.
Дата добавления: 2016-04-11; просмотров: 2189;
