Графическое представление данных
Графическое представление данных — это наиболее наглядное изображение полученного распределения результатов исследования. Оно дает возможность с одного взгляда определить структуру и состав изучаемой совокупности, структурные сдвиги, тенденции изменений при переходе от одних значений переменных к другим и т.д. При анализе социологической информации наиболее часто используют такие виды графического представления данных, как гистограмма, полигон и кумулята распределения, а также различные виды диаграмм (столбиковые, ленточные, секторные).
Гистограмма — это графическое изображение распределения, построенного чаще всего по интервальной шкале25. Гистограмма представляет собою ряд смежных прямоугольников, построенных на одной прямой: площадь каждого из них пропорциональна частоте нахождения данной величины в интервале, на котором построен данный прямоугольник. При равных интервалах плотности распределения пропорциональны частотам, которые и откладываются по оси ординат. Пример гистограммы, отражающей распределение опрошенных респондентов по возрасту, приведен на рис. 5.3.
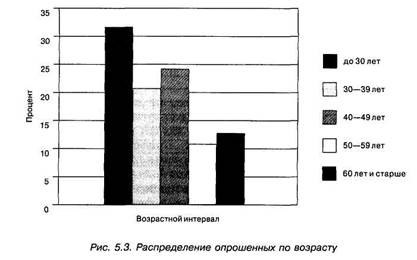
На этой гистограмме, построенной в Microsoft Excel в соответствии с данными табл. 5.10, удельный вес каждой возрастной категории в общем объеме выборочной совокупности выражается площадью прямоугольника, а общая площадь равна 1 (100%). Если бы мы строили гистограмму на основе абсолютных значений частот, то общая форма ее не изменилась бы, но в этом случае площадь каждого прямоугольника означала бы число лиц данной категории, а общая площадь была бы равна численности опрашиваемой совокупности (в данном случае — 812, поскольку мы не привели на гистограмме данные о тех, кто не указал в анкете своего возраста). Мы видим, например, что поскольку численность возрастной группы респондентов до 30 лет почти втрое больше численности респондентов в возрастном интервале 50—59 лет, то это выражается и в соответствующем соотношении высот столбцов.
Таблица 5.10
Распределение респондентов по возрастным группам
| Возрастная группа | Частота | Процент |
| 40 30 лет | 32,1 | |
| 30—39 лет | 20,5 | |
| 40—49 лет | 23,7 | |
| 50—59 лет | 10,2 | |
| 60 лет и старше | 12,2 | |
| Не указали | 1,3 | |
| Всего | 100,0 |
Обратим внимание на одну важную особенность гистограммы: протяженность по оси абсцисс должна соответствовать размеру отображаемого интервала. Этим гистограмма отличается, к примеру, от столбчатой (или столбиковой) диаграммы, где ширина столбца значения не имеет и просто фиксирует определенную позицию.
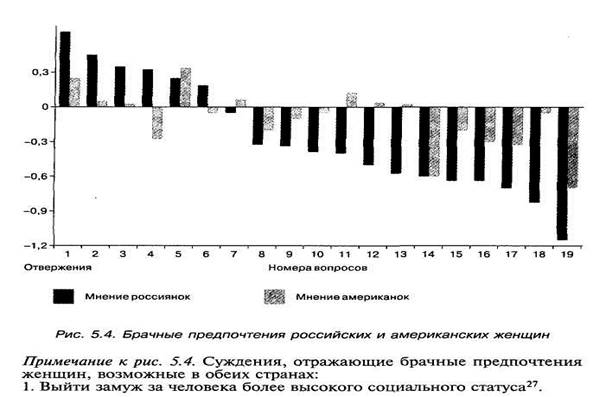
Перевод обычной таблицы в гистограмму сокращает мыслительный процесс, позволяет быстро и точно оценить ситуацию в целом. Гораздо реже встречаются ситуации, где гистограмма выполняет основную, а не вспомогательную роль. Если, к примеру, сравнивают удельный вес позитивных и негативных качеств у человека или социальной группы, располагая положительные выше горизонтальной оси, а негативные ниже, то можно получить прекрасную, почти живописную картину духовного мира человека. Подобно тому, как деревья отражаются в воде, так и негативные черты симметрично отражаются по ту сторону береговой линии, представленной осью ОХ. Похожую картину получили В.Ф.Петренко и О.В.Митина, исследовавшие стереотипы поведения россиянок и американок методом психосемантического анализа. Основной формой обработки исходных матриц данных у них было сопоставление ролевых позиций путем вычисления коэффициентов корреляций для пар ролевых позиций, т.е. вертикальных столбцов в матрице ранговых данных отдельно для российской выборки, отдельно для американской. В отношении брачных предпочтений у них получился график, представленный на рис. 5.4.
|
2. Выйти замуж за простого человека, хорошего хозяина, живущего «земными» проблемами.
3. Выйти замуж за человека другой национальности.
4. Выйти замуж за любимого человека с очень низкими доходами без перспективы их увеличить.
5. Выйти замуж за бизнесмена.
6. Выйти замуж за человека, посвятившего свою жизнь науке.
7. Выйти замуж за человека искусства (музыканта, поэта, артиста).
8. Выйти замуж за иностранца и уехать жить за границу.
9. Выйти замуж за военнослужащего.
10.Выйти замуж за политического деятеля.
11.Выйти замуж за рабочего.
12.Находиться на «содержании» у состоятельного мужчины.
13.Выйти замуж за «звезду» (спорта, эстрады, кино).
14.Выйти замуж без любви, по расчету.
15.Выйти замуж за фермера.
16.Выйти замуж за человека другой расы.
17.Не выходить замуж, полагая, что лучше прожить жизнь одной.
18.Выйти замуж за глубоко религиозного человека.
19.Выйти замуж за представителя криминальных структур.
Полигон распределения используется преимущественно для графического отображения распределений дискретных рядов (табл. 5.11). Эти графики строятся также в прямоугольной системе координат, в которой на горизонтальной оси х указываются значения (или ранг) переменной, а на вертикальной оси у отмечается общая численность или доля респондентов (в процентах), обладающая тем или иным значением.
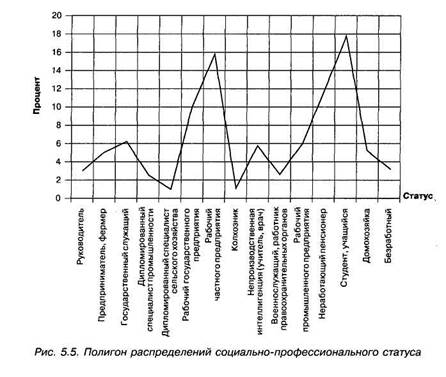
Полигоны могут использоваться и для изображения интервальных рядов. В этом случае ординаты, пропорциональные частоте каждого интервала, восстанавливаются перпендикулярно оси абсцисс из точек, соответствующих середине каждого интервала. Концы каждой из таких ординат соединяются прямыми линиями с концами соседних ординат (рис. 5.5).
Кумулята. Это еще один из способов графического изображения вариационных рядов. При построении кумуляты на оси абсцисс откладываются значения дискретных признаков (либо границы интервалов), а на оси ординат — накопленные частоты, соответствующие верхним границам частотных интервалов. Таким образом, отличие кумуляты от гистограммы состоит в том, что на графике кумуляты ординаты, пропорциональные частотам, последовательно накладываются одна на другую, так что высота последней ординаты соответствует сумме высот всех столбцов гистограммы. Ординаты соединяются прямыми линиями.
Таблица 5.11
Социально-профессиональный статус
| Категория | Частота | Процент |
| Руководитель | 3,0 | |
| Предприниматель, фермер | 4,6 | |
| Государственный служащий | 6,1 | |
| Дипломированный специалист промышленности | 2,8 | |
| Дипломированный специалист сельского хозяйства | 1,1 | |
| Рабочий государственного предприятия | 10,3 | |
| Рабочий частного предприятия | 15,9 | |
| Колхозник | 1,0 | |
| Непроизводственная интеллигенция (учитель, врач) | 5,8 | |
| Военнослужащий, работник правоохранительных органов | 2,7 | |
| Рабочий промышленного предприятия | 6,2 | |
| Неработающий пенсионер | 11,5 | |
| Студент, учащийся | 17,6 | |
| Домохозяйка | 4,7 | |
| Безработный | 3,3 | |
| Другие | 1,8 | |
| Не указали | 1,5 | |
| Всего | 100,0 |
Весьма наглядной выглядит кумулята, изображенная на рис. 5.6 — на основе распределения ответов на вопрос о среднедушевых доходах, задававшийся в том же исследовании.
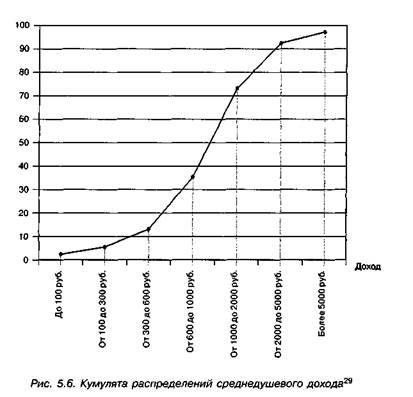
Кумулята позволяет быстро определить удельный вес той доли совокупности, которая находится выше или ниже некоторой заданной величины значения переменной. Так, по данным рис. 5.6, доля семейств, в которых месячный доход на одного члена семьи не превышает 2 тыс. руб., составляет 72,1%.
Диаграмма30 — это обобщенное название самых разнообразных графических изображений, наглядно показывающих соотношение каких-либо величин. Диаграммы по одним и тем же распределениям и вариационным рядам могут принимать множество различных видов и форм. Если вы откроете окно Мастер диаграммв программе Microsoft Excel, вы убедитесь, что там предлагается достаточно большой их набор: гистограммы, линейчатые, графики, круговые, точечные, кольцевые, пузырьковые и т.п. Выбор того или иного варианта — дело вкуса и чувства меры, поскольку в конечном счете каждая из них лишь по-разному — более или менее убедительно и, главное, наглядно — отображает выраженные в числовой форме ряды этих вариантов.
Дата добавления: 2016-04-11; просмотров: 825;
