Дифференциальная функция распределения

Для описания распределения вероятностей непрерывной случайной величины используется дифференциальная функция распределения.

Дифференциальная функция распределения (ДФР) (или плотность вероятности) – это первая производная от интегральной функции.

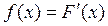
Интегральная функция распределения является первообразной для дифференциальной функции распределения. Тогда

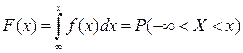
Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от дифференциальной функции, взятому в пределах от a до b:

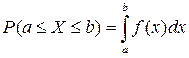
Геометрический смысл ДФР состоит в следующем: вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью x, кривой распределения f(x) и прямыми x = a и x = b (рис. 4).

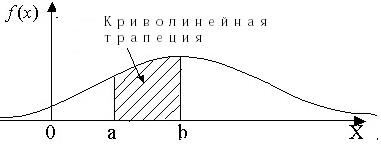
Рис. 4 График дифференциальной функции распределения принято называть кривой распределения.

Свойства дифференциальной функции распределения:

1. Дифференциальная функция распределения неотрицательна, т. е.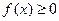

2. Если все возможные значения случайной величины принадлежат интервалу (a, b), то

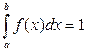
Дифференциальную функцию распределения часто называют законом распределения вероятностей непрерывных случайных величин.

При решении прикладных задач сталкиваются с различными законами распределения вероятностей непрерывных случайных величин. Часто встречаются законы равномерного и нормального распределения.