Закон распределения дискретной случайной величины. Элементы теории вероятностей

Элементы теории вероятностей

Случайные величины. Вероятность случайного события

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Обозначим: X, Y, Z – случайные величины

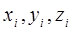– возможные значения случайных величин.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные возможные значения с определенными вероятностями.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины, независимо от величины промежутка, бесконечно.

Для задания дискретной случайной величины недостаточно перечислить все ее возможные значения, нужно указать еще и их вероятность.

Вероятность (Р) показывает степень возможности осуществления данного события, явления, результата.

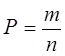, где n – общее число элементарных исходов (результатов испытания), m – число исходов, благоприятных случайному событию.

Вероятность невозможного события равна нулю, достоверного — единице (100%). Вероятность любого события лежит в пределах от 0 до 1 - в зависимости от того, насколько это событие случайно.

Закон распределения дискретной случайной величины

Законом распределения дискретной случайной величины называют соответствие между ее возможными значениями и вероятностями их появления. Закон распределения можно задать таблично, аналитически (в виде формулы) и графически (в виде многоугольника распределения).

Табличное задание закона распределения:

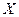
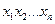- возможные значения случайной величины;

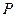
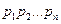- вероятности появления случайной величины.

Аналитическое задание закона распределения:

Биномиальное распределение, определяемое законом Бернулли

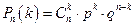
k = 0, 1, 2, …, n – количество возможных появлений событий

q = 1-p – вероятность не появления событий.

Распределение Пуассона, определяемое асимптотической формулой Пуассона:

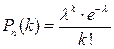
Где 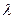- интенсивность потока событий.

Графическое задание закона распределения представлено на рис. 1

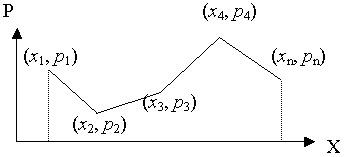
Рис. 1 Полигон распределения дискретной случайной величины.

Способ описания распределения случайной величины в виде таблицы, в виде формулы или графически применим только для дискретных случайных величин.