Тема 2.3. Практические расчеты на срез и смятие.
Детали соединений (болты, штифты, шпонки, заклепки) работают так, что можно учитывать только один внутренний силовой фактор — поперечную силу. Такие детали рассчитываются на сдвиг.
Сдвиг (срез)
Сдвигом называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор — поперечная сила рис. 23.1).
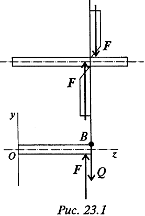
При сдвиге выполняется закон Гука, который в данном случав записывается следующим образом:
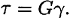
где 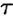 — напряжение;
— напряжение;
G — модуль упругости сдвига;
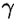 — угол сдвига.
— угол сдвига.
При отсутствии специальных испытаний G можно рассчитать по формуле,

гдеЕ — модуль упругости при растяжении, [G] = МПа.
Расчет деталей на сдвиг носит условный характер. Для упрощения расчетов принимается ряд допущений:
— при расчете на сдвиг изгиб деталей не учитывается, хотя силы, действующие на деталь, образуют пару;
— при расчете считаем, что силы упругости распределены по сечению равномерно;
— если для передачи нагрузки используют несколько деталей, считаем, что внешняя сила распределяется между ними равномерно.
Условие прочности при сдвиге (срезе)
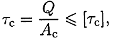
где [  ] — допускаемое напряжение сдвига, обычно его определяют по формуле
] — допускаемое напряжение сдвига, обычно его определяют по формуле
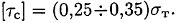
При разрушении деталь перерезается поперек. Разрушение детали под действием поперечной силы называют срезом.
Смятие
Довольно часто одновременно со сдвигом происходит смятие боковой поверхности в месте контакта в результате передачи нагрузки одной поверхности к другой. При этом на поверхности возникают сжимающие напряжения, называемые напряжениями смятия, 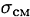 .
.
Расчет также носит условный характер. Допущения подобны принятым при расчете на сдвиг, однако при расчете боковой цилиндрической поверхности напряжения по поверхности распределены не равномерно, поэтому расчет проводят для наиболее нагруженной точки. Для этого вместо боковой поверхности цилиндра в расчете используют плоскую поверхность, проходящую через диаметр.
Условие прочности при смятии

гдеАсм-расчетная площадь смятия
Асм = 
d — диаметр окружности сечения;
 — наименьшая высота соединяемых пластин;
— наименьшая высота соединяемых пластин;
F — сила взаимодействия между деталями
[ 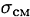 ]-допускаемое напряжение смятия
]-допускаемое напряжение смятия
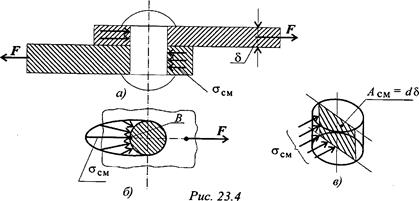
[ 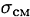 ] = (0,35 + 0,4)
] = (0,35 + 0,4) 
Тема 2.5. Кручение
Кручение – вид нагружения бруса, при котором в его поперечных сечениях возникает один внутренний силовой фактор – крутящий момент Мкр.
Крутящий момент Мкр в произвольном поперечном сечении бруса равен алгебраической сумме моментов, действующих на отсеченную часть бруса.
Крутящий момент считается положительным, если кручение происходит против часовой стрелки и отрицательны – по часовой стрелке.
При расчете валов на прочность при кручении используется условие прочности:
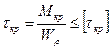 ,
,
где 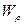 - полярный момент сопротивления сечения, мм3;
- полярный момент сопротивления сечения, мм3;
[  ] – допускаемое касательное напряжение.
] – допускаемое касательное напряжение.
Крутящий момент определяется по формуле:
 ,
,
где Р – мощность на валу, Вт;
ω – угловая скорость вращения вала, рад/с.
Полярный момент сопротивления сечения определяется по формулам:
- для круга

- для кольца
 .
.
При кручении бруса его ось испытывает скручивание на некоторый угол φ, который называется углом закручивания. Его величина определяется по формуле:
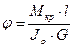 ,
,
где l – длина бруса;
G – модуль сдвига, МПа (для стали G=0,8·105МПа);
 - полярный момент инерции сечения, мм4.
- полярный момент инерции сечения, мм4.
Полярный момент инерции сечения определяется по формулам:
- для круга
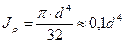
- для кольца
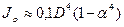 .
.
Тема 2.6. Изгиб
Многие элементы конструкций (балки, рельсы, оси всех колес и т.д.) испытывают деформацию изгиба.
Изгибом называется деформация от момента внешних сил, действующих в плоскости, проходящей через геометрическую ось балки.
В зависимости от места приложения действующих сил различают прямой и косой изгиб.
Прямой изгиб– внешние силы, действующие на балку, лежат в главной плоскости сечения.
Главная плоскость сечения – плоскость, проходящая через ось балки и одну из главных центральных осей сечения.
Косой изгиб - внешние силы, действующие на балку, не лежат в главной плоскости сечения.
В зависимости от характера ВСФ, возникающих в поперечных сечениях балки, изгиб может быть чистым и поперечным.
Изгиб называется поперечным, если в поперечном сечении балки возникают два ВСФ – изгибающий момент Мх и поперечная сила Qy.
Изгиб называется чистым, если в поперечном сечении балки возникает один ВСФ – изгибающий момент Мх.
Изгибающий момент в произвольном сечении равен алгебраической сумме моментов внешних сил, действующих на отсеченную часть балки:

Поперечная сила Q равна алгебраической сумме проекций внешних сил, действующих на отсеченную часть балки:
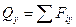 .
.
При определении знаков поперечных сил используют правило «Часовой стрелки»: поперечная сила считается положительной, если «вращение» внешних сил происходит по часовой стрелке; отрицательной – против часовой стрелки.
При определении знаков изгибающих моментов используют правило «Сжатых волокон» (правило «ЧАШИ»): изгибающий момент считается положительным, если сжимаются верхние волокна балки («вода не выливается»); отрицательным, если сжимаются нижние волокна балки («вода выливается»).
Условие прочности при изгибе:рабочее напряжение должно быть меньше или равно допускаемому напряжению, т.е.
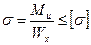
где Wх – осевой момент сопротивления (величина, характеризующая способность элементов конструкции сопротивляться деформации изгиба), мм3.
Осевой момент сопротивления определяется по формулам:
- для круга
 ;
;
- для кольца
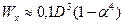 ;
;
- для прямоугольника

 .
.
При прямом поперечном изгибе изгибающий момент обуславливает возникновение нормального напряжения, а поперечная сила – касательного напряжения, которое определяется по формуле:
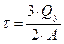 ,
,
где А – площадь поперечного сечения, мм2.
Дата добавления: 2016-04-11; просмотров: 1601;
