Математические модели роста отдельной популяции. Анализ модели «хищник-жертва». Фазовые портреты.

Модели роста отдельной популяции.

Уравнение логистической кривой Ферхюльста получается при учете самоограничения роста популяции в условиях тесноты и конкуренции внутри популяции. Оно имеет вид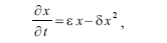

Уравнения стационарных состояний

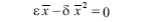
Имеет два корня

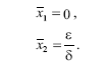
Согласно критерию устойчивости знак производной правой части

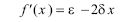
В стационарной точке определяет ее устойчивость.

Подставив значение х₁=0 получим что 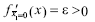, тоесть состояние неустойчиво.

Другое состояние (х₂) устойчиво, так как всегда

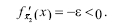
Устойчивое состояние 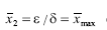соответствует максимальной ччивленности популяции, или емкости среды, возможной в данныйх условиях.Как видно, величина зависит от соотеошения костант эпсилони сигма, притока и убыли численности популяции.

Уравнение удобно переписать в виде

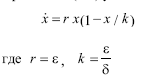
Если мы берем разнополую популяцию, то, при условии неограниченных ресурсов скорость размножения определяется числом встреч самцов и самок и квадратично растет с ростом числа особей

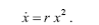
Однако когда плотность популяции очень велика, скорость размножения лимитируется не числом встреч самцов и самок, а числом часмок в популяции. Оба эффекта – квадратичная зависимость скорости размножения и ее некоторое ограничение при больших плотностях учитывается как

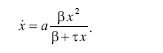
Введя член, описывающий смертность, пропорциональную численности, получим

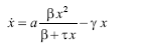
Это уравнение имеет два стационарных решения

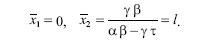
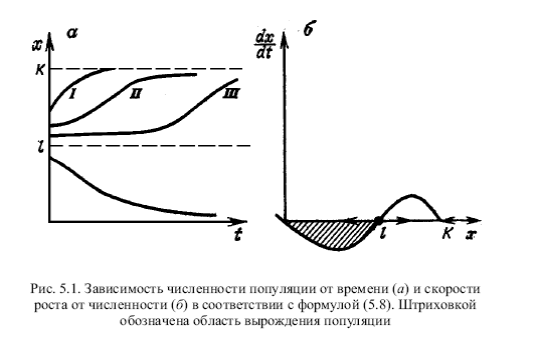
Точка х₁=0 устойчива, а точка х₂= l – неустоцчива. Если начальная популяция по численности меньше l, то популяция вырождается и ее численность стремится к нулю. При размере популяции больше l она растет неограниченно.

Введем ограничение сверху.

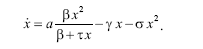
Модель Хищник – жертва.

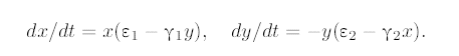
Найдем координаты особой точки, прировняв правые части к нулю. Это дает стационарные ненулевые значения

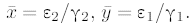
Линеаризация системы вблизи точки 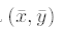дает

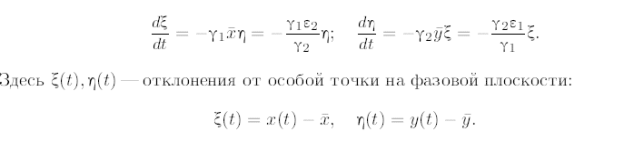
Характеристическое уравнение системы

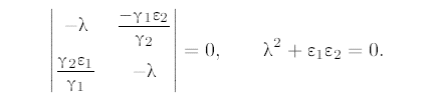
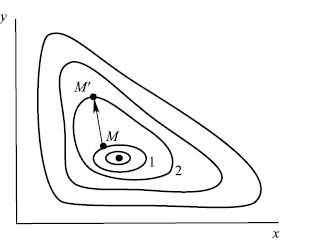
Корни уравнения чисто мнимые, 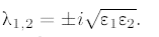тип особой точки – центр.