Ингибирование ферментативных реакций

Конкурентное – ингибитор (I) связывается с реакционным центром фермента. Помимо активного комплекса ES образуется неактивный комплекс EI

E + S ↔ ES →E + P

E + I _k-i↔^k+I EI

С учётом сохранения числа частиц: S +P = So; E +[ES] + [EI] = Eo

Равновесная концентрация неактивного комплекса определяется из соотношения

Ki = k-i/ k+i = E*I/[EI], откуда [EI] = E*I/Ki. С учётом последнего, переписываем условие сохранения молекул фермента в виде:

Eo = E + [ES] + EI/Ki = [ES] + E(1 + I/Ki), откуда

E = (Eo – [ES])/(1 + I/Ki)

При условии квазистационарного приближения d[ES]/dt = 0, d[EI]/dt = 0

Подставляем выражение для Е в уравнение

D[ES]/dt = k1*S*E – k-1*[ES] – k+2[ES] = 0

и решая относительно [ES], получаем:

[ES] = (Eo*S)/(Km+S+(Km*I)/Ki)

υ = dP/dt = (k+2*Eo*S)/(Km+S+(Km*I/)Ki)

Частный случай – конкурентное ингибирование продуктом: E + P _k-3↔^k3 EP

υ = (k+2*Eo*S)/(Km+S+(Km*P/)Kp), где Kp = k-3/k+3

Неконкурентное – ингибитор связывается с аллостерическим центром, угнетая его активность: E+I ↔^Ki EI, ES+I ↔^Ki ESI (Ki не зависит от того, связан ли фермент с субстратом)

υ = (k+2*Eo*S)/[(Km+S)*(1+I/Ki)]. При S>>Km получаем

υ^max = (k+2*Eo)/(1+I/Ki)

Открытая система с субстратным угнетением – включает в себя реакцию притока субстрата, оттока продукта и образование неактивного комплекса.

So→^k S +E _k-1↔^k1 ES →^k2 E+P →^k4

ES + S _k-3↔^k3 ES²

Скорость образования продукта в данной схеме:

υ_p = (k2*Eo*S)/(Km +S+[S²/ks]), где ks = k3/k-3

При S<<1 величиной S²/ks можно пренебречь – уравнение совпадает с уравнением Михаэлиса-Ментен. При S→∞ образуется неактивный комплекс и υ_p→0. График зависимости υ_p(S) имеет вид колоколообразной кривой с максимумом и последующим асимптотическим приближением к нулю

/Не уверен, что написанное ниже нужно в этом вопросе, так что решайте сами/

Скорость изменения концентрации субстрата S складывается из скорости притока (υ_прит=k(So –S) = α – kS) и оттока в ходе ферментативной реакции:

υ_s = υ_прит - υ_p

В стационарном состоянии υ_прит - υ_p = 0

Стационарные точки S являются пересечением кривых υ_p(S) и υ_прит (S)

Рисунок 3

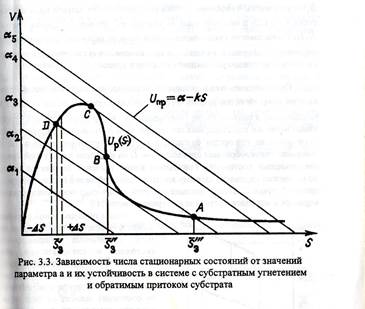
В интервале α2< α < α4 система имеет три различных стационарных состояния, а значения α2 и α4, при которых изменяется число стационарных точек, являются бифуркационными.

Проверим устойчивость точек. Зададим смещение от точки S3’ влево. Мы видим, что скорость притока субстрата стала больше скорости его оттока (тонкая линия над толстой кривой). При смещении вправо наоборот υ_p(S) > υ_прит (S)=> система стремиться вернуться в эту точку. Аналогично находим, что S3’’ неустойчива, а S3’’’ – устойчива. Устойчивые точки расположены на кривой υ_p(S) на участках AB и CD, а неустойчивые – на участке BC

Построим график зависимости стационарных состояний от управляющего параметра α:

Рисунок 4

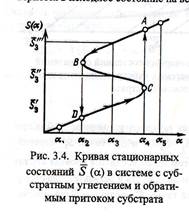
Здесь есть два устойчивых участка – система может работать в двух режимах. При попадании на неустойчивый участок система совершает перескок (см направление стрелок на рисунке) Таким образом, система является триггерной. Направление переходов и реализация одного или другого устойчивого состояния зависят от того, происходит ли увеличение или уменьшение параметра (по какой ветке движется система). Это свойство системы – совершать разными путями переход из одного состояния в другое в зависимости от предыстории системы называется гистерезисом.Периодическое движение вдоль гистерезисного цикла носит колебательный характер: A→B→D→C→A

Колебания при субстратном и продуктном неконкурентном угнетении:

S+ES↔ESS

P+ES↔ESP

P+E↔EP

P+ESS↔ESSP

Схема реакции – рисунок 5

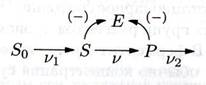
dS/dt = υ1 – υ(S,P)

dP/dt = υ(S,P) – υ2

Число и устойчивость стационарных состояний данной системы зависят от глубины продуктного угнетения При слабом угнетении концентрация субстрата будет быстрой переменной по сравнению с концентрацией продукта. При этом реализуется единственное неустойчивое стационарное состояние на неустойчивой части характеристики υ(S) (отрезок АВ) Автоколебания возникают на фазовой плоскости S, P при движении вдоль цикла С→A→D→B→C

Рисунок 6

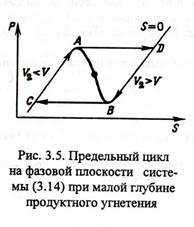
Движение по устойчивой ветке СА совершается с накопление продукта. В критической точке А при υ2 = υ система скачком переходит в точку D ветви DB, где концентрация продукта начинает убывать, а скорость υ растёт. В точке В при υ2 = υ система вновь срывается и уходит в точку С