Кинетика простейших ферментативных реакций. Уравнение Михаэлиса-Ментен. Влияние ингибиторов на кинетику ферментативных реакций.

Рассмотрим реакцию

E + S _k-1↔ ^k1 (ES) →^k2 E + P

где S – субстрат, P – продукт, E – фермент, ES – фермент-субстратный комплекс; k1 k-1 – константы прямой и обратной реакций образования комплекса, k2 – константа скорости образования продукта (при малых концентрациях Р эта реакция необратима). k2 показывает число актов катализа в единицу времени – число оборотов фермента.

Эта система описывается следующими уравнениями:

dS/dt = – k1 (S)(E) + k-1 (ES)

dE/dt = – k1 (S)(E) + k-1 (ES) + k2 (ES)

d(ES)/dt = k1 (S)(E) – k-1 (ES) – k2 (ES)

dP/dt = k2 (ES) = υ_p

Сложим второе и третье уравнения системы. Получим, что d(E + ES)/dt = 0=> в любой момент времени (E) + (S) = Eo (общая концентрация фермента) и что dE/dt = – d(ES)/dt. Можем выразить Е = Ео – (ES). Заметим, что четвёртое уравнение определяется переменной ES. Значит, можем решать систему из двух уравнений:

dS/dt = – k1 [Ео – (ES)] + k-1 (ES)

d(ES)/dt = k1 (S) [Ео – (ES)] – k-1 (ES) – k2 (ES)

Посмотрим, можно ли разделить переменные на медленные и быстрые. Характерное время изменения субстрата τs = S/υ_p (υ_p - скорость ферментативной реакции) Скорость становится максимальной, когда весь фермент (Ео) находится в связанном состоянии: υ_p^max = k2 Eo. При этом время убыли S будет минимальным: τs^min = S/( k2 Eo). Характерное время оборота фермента определяется в основном реакцией распада ES и константой k2 (k2>> k1). Оно равно τ_E = 1/k2.

В обычных условиях концентрация субстрата во много раз больше концентрации фермента (обычно Eo = 10^-6M, S = 10^-2M). Значит, Eo/S = 10^-4<<1, Следовательно, τs^min=τ_E/(10^-4) = τ_E*10⁴

Отсюда τs>> τ_E => переменная S меняется медленнее, чем ES => скорость изменения субстрата мала по сравнению со скоростью изменения комплекса. Значит, при рассмотрении системы на больших отрезках времени можно считать, что d(ES)/dt = 0. Получаем алгебраическое уравнение:

k1 (S) [Ео – (ES)] – k-1 (ES) – k2 (ES) = 0

Отсюда

ES = (k1*S*Ео)/(k1*S + k-1+ k2) ó

ó υ_p = k2*ES = (k1*k2*S*Ео)/(k1*S + k-1+ k2)

Поделим числитель и знаменатель правой части на k1:

υ_p = (k2*S*Ео)/(S + [k-1+ k2]/ k1) = (k2*S*Ео)/(S + Km) – уравнение Михаэлиса-Ментен

Методы определенияυ_p^max и Km(в биофизике этого толком нет, так что взял из биохимии)

1. При S→∞, υ→ υ_p^max = k2 Eo (оптимальная концентрация S для данного способа – 10Km). При Km=S, υ= υ_p^max/2

Рисунок 1

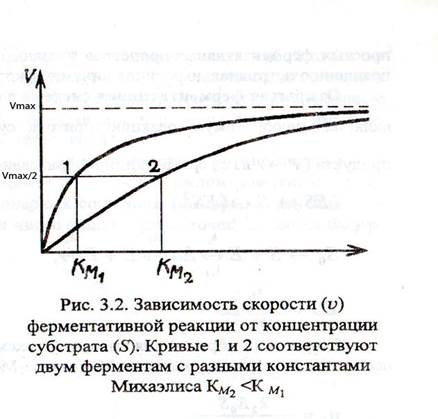
2. Линеаризация уравнения:

1/ υ = (S + Km)/( υ_p^max*S) = 1/ υ_p^max +(Km/ υ_p^max)*(1/S)

Рисунок 2

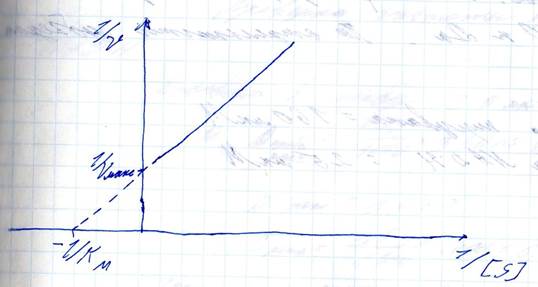
При S→∞, 1/S→0 => 1/υ=1/ υ_p^max

При 1/ υ=0, 1/ υ_p^max= – (Km/ υ_p^max)*(1/S) => S= - Km