Селекция и генетический выигрыш

В настоящем разделе речь пойдет не о селекции как науке вообще, я только об эффективности одного из ее методов, а именно отбора в генетическом смысле. Целью отбора является выбор индивидуумов с желательными признаками, которые могут использоваться в качестве родителей для следующих генераций потомков.

Селекция базируется на том, что средняя генетическая ценность отбираемых индивидуумов будет лучше, чем средняя ценность индивидуумов популяции в целом. Для мерных, или количественных, признаков выигрыш от селекции обычно измеряется по изменению популяционной сред-

ней. Улучшение, которое потенциально может быть достигнуто в результате селекции для определенного признака, есть функция наследуемости признака и изменчивости признака, которая существует в популяции (П. Ф. Рокицкий, 1978; В. Zobel, J. Talbert, 1984; Д. С. Фолконер, 1985).

Значение наследуемости в определении ответа на отбор было показано ранее. Высокая наследуемость показывает, что большая часть изменчивости, наблюдаемой в популяции для данного признака, является генетической по происхождению, и что селекционер имеет высокую вероятность выбора родителей с генетически обусловленными желательными фенотипами.

Общая величина изменчивости признака так же важна, как и наследуемость при оценке выигрыша, который может быть получен от селекции, - однако этот фактор нередко игнорируется людьми, занимающимися селекцией. Общая, или фенотипическая, вариация важна ввиду ее влияния на селекционный дифференциал.

Селекционный дифференциал S является средней фенотипической ценностью отбираемых индивидуумов, выраженной как отклонение от популяционной средней. Если для данного признака в популяции существует высокая фенотипическая изменчивость, то селекционный дифференциал может быть большим. Если же общая изменчивость минимальна, то и селекционный дифференциал может быть небольшим. Селекционный дифференциал S может быть определен с помощью графика (рис. 12.3) как разница между средней величиной признака для популяции в_ целом (X) и средней величиной того же признака в отбираемой группе (Xs). Заштрихованная область на рис. 12.3 показывает группу индивидуумов, которые отбираются в качестве родителей для использования в последующих генерациях потомков

Таким образом, селекционный дифференциал S представляет собой разницумежду средней величиной признака в отбираемой группе индивидуумов Xs и популяционной средней X:

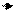
S = X_S - X. (12.11)

Когда отбор индивидуумов основывается только на их фенотипических значениях, без информации о степени родства, ответ на селекцию R может быть оценен по следующей формуле:

генетический выигрыш = наследуемость в узком смысле х селекционный дифференциал,

или R = h²S. (12.12)

Из приведенной формулы видно, что средняя величина потомства от отобранных родителей не может быть выше средней величины отобранной группы родителей, и обычно она меньше. Это объясняется следующими причинами:

1) Обычно только часть превосходства отселектированных родителей обусловлена генетически. Другая часть обусловлена условиями место произрастания. Превосходство, обусловленное условиями место произрастания, не может быть передано от родителей к потомкам. Например, отобранные родители могут иметь превосходство над их соседями потому, что они росли в несколько лучших микроусловиях.

2) В программах улучшения популяций, где отселектированные родители спариваются между собой, может использоваться только аддитивная генетическая дисперсия. По этой причине и в вышеприведенной формуле используется наследуемость в узком смысле. Даже если бы вся наблюдаемая изменчивость была генотипического происхождения (изменчивость, обусловленная средой, отсутствовала), то выигрыш был бы равен селекционному дифференциалу только в том случае, если бы вся генетическая изменчивость была аддитивной и совершенно отсутствовала неаддитивная изменчивость, т. е. h² = 1.

Селекционер может воздействовать на выигрыш от селекции по существу двумя путями. Первый — исходная популяция может управляться так, Чтобы максимизировать наследуемость путем унифицирования условий место роизрастания и контроля за условиями среды. Это основной фактор, который используется в селекционных схемах и при планировании создания испытательных генетических объектов. Однако, если популяция уже создана в данных условиях, селекционеру трудно повлиять на увеличение наследуемости.

Большие возможности увеличения выигрыша от селекции могут быть получены также путем увеличения селекционного дифференциала. Этот

путь более приемлем для естественных насаждений. Обычно оценки наследуемости для деревьев в естественных насаждениях низки, особенно для признаков роста (высота, диаметр и т. д.), ввиду высокой экологической изменчивости, включая конкуренцию. Однако отдельные деревья существенно отличаются друг от друга, и селекционный дифференциал может быть очень высоким.

Селекционный дифференциал зависит от двух факторов. Один — это доля индивидуумов, которая отбирается из популяции и которая отражает интенсивность селекции i. Второй фактор — это фенотипическое стандартное отклонение σ_p

Интенсивность отбора i может быть выражена в долях стандартного отклонения след. формулой:

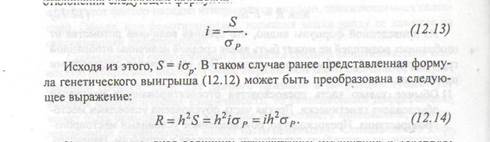
Следовательно, зная величину стандартного отклонения и заданную интенсивность отбора (а также наследуемость селекционируемого признака), можно предсказать величину генетического выигрыша до проведения самого процесса отбора. Наоборот, варьируя интенсивность селекции в зависимости от количества отбираемых индивидуумов, можно получить желательную величину выигрыша. Таким образом, интенсивность селекции связана с долей индивидуумов, которые отбираются из популяции. Если эта доля известна, то расчет можно осуществлять на основе этой величины. Для облегчения этой операции в табл. 12.4 приведена величина интенсивности селекции в зависимости от уровня селекции (величины отбираемой доли из популяции) и размера популяции (при условии нормального распределения признака).

Таким образом, отметим еще раз, что ответ на селекцию (по какому-либо признаку) зависит от двух факторов: наследуемости признака и селекционного дифференциала. Для достижения большего генетического выигрыша селекционер должен пытаться увеличить оба этих показателя. Причем в искусственных популяциях большие возможности можно получить за счет увеличения первого показателя (/г2), а в естественных — за счет увеличения второго (S).

Вопросы для самопроверки

1. Что представляет собой средняя величина какого-либо признака популяции? Приведите формулу ее расчета.

2.Что такое варианса, или дисперсия? Приведите формулу ее расчета.

3.Дайте определение коэффициента изменчивости или вариации. Формула для его вычисления.

4.Приведите шкалу уровней изменчивости признаков лесных древесных пород по С. А. Мамаеву.

3, Как выражается истинное среднее популяции? Приведите формулу. & Что такое ОКС и как она определяется? Какой тип действия генов она отражает? Где она может быть реализована?

7,Как выразить селекционную ценность дерева через ОКС?

8,Что такое СКС и как она определяется? Какое взаимодействие генов она отражает? Как можно использовать СКС в селекционных программах?

9,Дайте определение понятию «наследуемость»? В чем различие понятий наследуемости * широком и в узком смысле? Формулы для их определения.

I0. Приведите примеры оценки наследуемости в узком смысле для отдельных признаков и видов лесных древесных пород.

11. Что такое селекционный дифференциал? Как можно его представить графически и аналитически? 12.Что такое селекционный выигрыш? Формула его определения. П. Явчечу средняя величина потомства от совокупности отобранных родителей, как правило, не может быть больше средней величины этих родителей?

14 Никнем пути увеличения выигрыша от селекции?

I Чти такое интенсивность селекции и как с ее помощью можно увеличить генетический

Выигрыш?

195