Обтекание круглого цилиндра

Комплексный потенциал, включающий сумму потенциалов плоскопараллельного оси Х потока и диполя, можно записать

(6.54)

Отделив мнимую и вещественную части запишем из

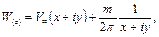(6.55)

Выражения для потенциала скорости и функции тока с учетом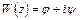

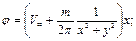(6.56)

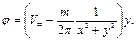(6.57)

Следовательно, уравнение линии тока будет 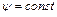или

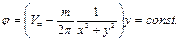(6.58)

Нулевая линия тока 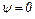задается двумя уравнениями

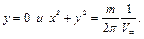(6.59)

Второе уравнение представляет собой окружность радиуса

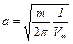(6.60)

с центром в начале координат. Первое соответствует оси абсцисс (рис. 6.7).

Рис. 6.7. Линии тока при обтекании круглого цилиндра

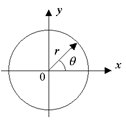
Рис. 6.8. Цилиндрические координаты (полярные в сечении)

Заменив нулевую линию тока твердой стенкой без изменения характера движения потока получим обтекание круглого цилиндра.

В цилиндрических координатах запишем равенства 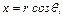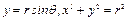(рис. 6.8) и

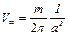, (6.61)

поэтому

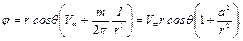(6.62)

Проекции скорости будут

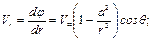(6.63)

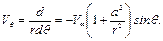(6.64)

На поверхности цилиндр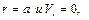а

а 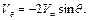(6.65)

Точки, в которых скорость равна нулю при обтекании цилиндра, соответствуют 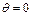и 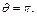Максимальные значения скоростей соответствуют 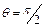и

Из уравнения Бернулли для нулевой линии тока получим

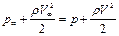(6.67)

или

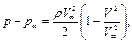(6.68)

где p - давление в любой точке на поверхности цилиндра.

Вводя коэффициент давления

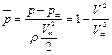, (6.69)

и подставляя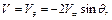

Получим

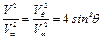(6.70)

Поэтому

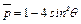(6.71)

Рис. 6.9. Распределение коэффициента давления

Обтекание реальной жидкостью круглого цилиндра ведет к несимметричному распределению давления. Вид кривой распределения давления зависит от числа Рейнольдса Re.

Проекции сил давления, действующего на элементарную площадку 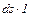(единичной длины) будут равны:

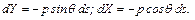(6.72)

Поскольку

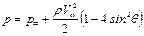(6.73)

и

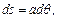(6.74)

то

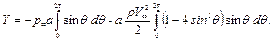(6.75)

Учитывая

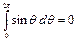и 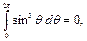(6.76)

получим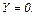

Аналогично доказывается, что и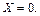

Отсутствие силы сопротивления для тел, независимо от их формы, обтекаемых потоком идеальной жидкости, в гидродинамике называется парадоксом Даламбера.