Для решения задач гидродинамики
Плоское стационарное движение жидкости
При плоском стационарном движении жидкости все ее частицы перемещаются параллельно некоторой плоскости (рис. 6.1)
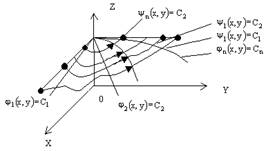
Рис. 6.1. Плоское движение жидкости
Если определяющая плоскость совпадает с координатной 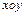 , то потенциал скорости будет равен
, то потенциал скорости будет равен 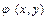 , а уравнения
, а уравнения
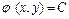 (6.1)
(6.1)
будут линиями эквипотенциалей.
Компоненты скорости в проекциях на оси 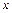 и
и 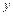 определяются в виде
определяются в виде
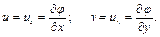 (6.2)
(6.2)
Уравнение неразрывности в случае плоского движения жидкости имеет вид
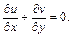 (6.3)
(6.3)
Если ввести функцию 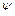 , связанную с проекциями скоростей равенствами
, связанную с проекциями скоростей равенствами
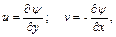 (6.4)
(6.4)
то она удовлетворяет уравнениям неразрывности, т.к.
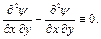 (6.5)
(6.5)
Эта функция называется функцией тока, а выражение 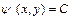 является уравнением линий тока.
является уравнением линий тока.
Поскольку уравнение безвихревое, то
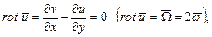 (6.6)
(6.6)
поэтому
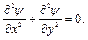 (6.7)
(6.7)
Подстановка равенств 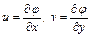 в уравнение неразрывности дает
в уравнение неразрывности дает
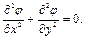 (6.8)
(6.8)
Сравнение равенств (6.2) и (6.4) дает
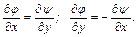 (6.9)
(6.9)
Функции, удовлетворяющие условиям (6.9), называются гармоническими.
Применение теории функций комплексной переменной
для решения задач гидродинамики
В теории комплексной переменной связь между функциями 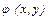 и
и 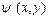 называется условиями Коши-Римана.
называется условиями Коши-Римана.
При этом комплексная величина 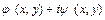 является комплексной переменной
является комплексной переменной 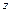 , равной
, равной 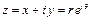 (рис. 6.2).
(рис. 6.2).
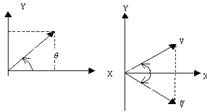
Рис. 6.2. Определение комплексной переменной 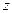 и
и 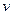
Таким образом, существует функция комплексной переменной 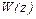 , вещественная и мнимая части которой будут
, вещественная и мнимая части которой будут 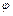 и
и 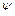 , т.е.
, т.е.
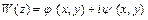 . (6.10)
. (6.10)
Функция 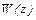 называется комплексным потенциалом или характеристической функцией течения.
называется комплексным потенциалом или характеристической функцией течения.
Производная 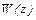 не зависит от направления дифференцирования (условие аналитичности) и полностью определяется положением точки в плоскости
не зависит от направления дифференцирования (условие аналитичности) и полностью определяется положением точки в плоскости 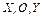 , заданной координатой
, заданной координатой 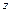 , т.е.
, т.е.
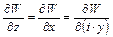 (6.11)
(6.11)
или
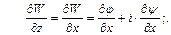 (6.12)
(6.12)
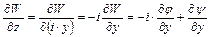 . (6.13)
. (6.13)
С учетом условий 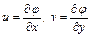 и
и 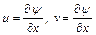 получим
получим
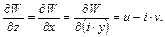 (6.14)
(6.14)
Величина и направление скорости 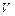 в комплексной плоскости (рис.6.2) определится формулой
в комплексной плоскости (рис.6.2) определится формулой
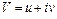 (6.15)
(6.15)
Производная от комплексного потенциала по координате равна скорости по абсолютной величине, а по направлению совпадает с зеркальным отображением вектора скорости относительно вещественной оси.
Величина 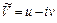 называется сопряженной скоростью.
называется сопряженной скоростью.
Плоскость 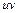 является плоскостью годографа скорости.
является плоскостью годографа скорости.
Значение контурного интеграла равно
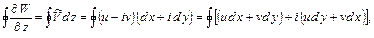 (6.16)
(6.16)
но
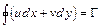 , (6.17)
, (6.17)
а
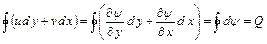 . (6.18)
. (6.18)
Здесь 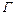 - циркуляция скорости по замкнутому контуру;
- циркуляция скорости по замкнутому контуру; 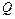 - объемный расход через замкнутый контур.
- объемный расход через замкнутый контур.
Для действительной части получим
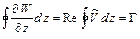 , (6.19)
, (6.19)
а для мнимой

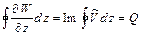 . (6.20)
. (6.20)
Можно поставить две задачи:
1) по заданному комплексному потенциалу найти 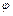 ,
, 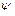 и поле скоростей;
и поле скоростей;
2) зная контур обтекаемого тела и значение скорости на бесконечности, найти комплексный потенциал.
Дата добавления: 2016-02-16; просмотров: 1151;
