4 страница. 3. По идентификатору IDi выделяется вектор Si.
3. По идентификатору IDi выделяется вектор Si.
4. Субъект аутентификации запрашивает у пользователя аутентификатор К.
5. Субъект аутентификации вычисляет значение Y= F(Si, К).
6. Субъект аутентификации производит сравнение значений Y и Еь При совпадении этих значений устанавливается, что данный пользователь успешно аутентифицирован в системе. В противном случае аутентификация отвергается - пользователь не допускается к работе.
Вторая схема аутентификации применяется в ОС UNIX. В качестве идентификатора ID используется имя пользователя (запрошенное по Loqin), в качестве аутентификатора К - пароль пользователя (запрошенный по Password), функция F представляет собой алгоритм шифрования DES. Эталоны для идентификации и аутентификации содержатся в файле Etc/passwd.
Следует отметить, что необходимым требованием устойчивости схем аутентификации к восстановлению информации Ki является случайный равновероятный выбор Ki из множества возможных значений.
Системы парольной аутентификации имеют пониженную стойкость, поскольку в них выбор аутентифицирующей информации происходит из относительно небольшого множества осмысленных слов. Мощность этого множества определяется энтропией соответствующего языка.
Особенности применения пароля для аутентификации пользователя
Традиционно каждый законный пользователь компьютерной системы получает идентификатор и/или пароль. В начале сеанса работы пользователь предъявляет свой идентификатор системе, которая затем запрашивает у пользователя пароль.
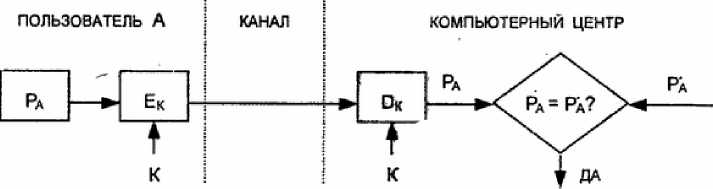
Простейший метод подтверждения подлинности с использованием пароля основан на сравнении представляемого пользователем пароля РА С исходным значением РА', хранящимся в компьютерном центре (рис. 2.1). Поскольку пароль должен храниться в тайне, он должен шифроваться перед пересылкой по незащищенному каналу. Если значения РА и РА' совпадают, то пароль РА считается подлинным, а пользователь - законным.
 (ПАРОЛЬ ПОДЛИННЫЙ)
Рисунок 2.1 - Схема простой аутентификации с помощью пароля
(ПАРОЛЬ ПОДЛИННЫЙ)
Рисунок 2.1 - Схема простой аутентификации с помощью пароля
|
Если кто-нибудь, не имеющий полномочий для входа в систему, узнает каким-либо образам пароль и идентификационный номер законного пользователя, он получает доступ в систему.
Иногда получатель не должен раскрывать исходную открытую форму пароля. В этом случае отправитель должен пересылать вместо открытой формы пароля отображение пароля, получаемое с использованием односторонней функции a(.) пароля. Это преобразование должно гарантировать невозможность раскрытия противником пароля по его отображению, так как противник наталкивается на неразрешимую числовую задачу.
Например, функция a(.) может быть определена следующим образом:
a(P)Ep(ID),
где Р - пароль отправителя; ID-идентификатор отправителя; ЕР - процедура шифрования, выполняемая с использованием пароля Р в качестве ключа.
Такие функции особенно удобны, если длина пароля и ключа одинаковы. В этом случае подтверждение подлинности с помощью пароля состоит из пересылки получателю отображения а(Р) и сравнения его с предварительно вычисленным и хранимым эквивалентом а'(Р).
На практике пароли состоят только из нескольких букв, чтобы дать возможность пользователям запомнить их. Короткие пароли уязвимы к атаке полного перебора всех вариантов. Для того чтобы предотвратить такую атаку, функцию а(Р) определяют иначе, а именно:
а(Р)=Ерр+к(ГО),
где К и ID-соответственно ключ и идентификатор отправителя.
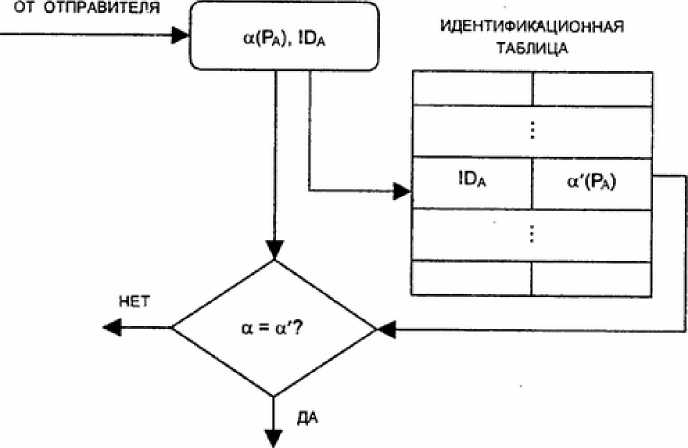
Очевидно, значение а(Р) вычисляется заранее и хранится в виде а'(Р) в идентификационной таблице у получателя (рис. 2.2). Подтверждение
подлинности состоит из сравнения двух отображений пароля а(РА) и а'(РА) и признания пароля РА, если эти отображения равны.
|
Рисунок 2.2 - Схема аутентификации с помощью пароля с использованием идентификационной таблицы
Конечно, любой, кто получит доступ к идентификационной таблице, может незаконно изменить ее содержимое, не опасаясь, что эти действия будут обнаружены.
Биометрическая идентификация и аутентификация пользователя
Процедуры идентификации и аутентификации пользователя могут базироваться не только на секретной информации, которой обладает пользователь (пароль, секретный ключ, персональный идентификатор и т.п.). В последнее время все большее распространение получает биометрическая идентификация и аутентификация пользователя, позволяющая уверенно идентифицировать потенциального пользователя путем измерения физиологических параметров и характеристик человека, особенностей его поведения.
Отметим основные достоинства биометрических методов идентификации и аутентификации пользователя по сравнению с традиционными:
• высокая степень достоверности идентификации по биометрическим признакам из-за их уникальности;
• неотделимость биометрических признаков от дееспособной личности;
• трудность фальсификации биометрических признаков.
В качестве биометрических признаков, которые могут быть использованы при идентификации потенциального пользователя, можно выделить следующие:
• узор радужной оболочки и сетчатки глаз;
• отпечатки пальцев;
• геометрическая форма руки;
• форма и размеры лица;
• особенности голоса;
• биомеханические характеристики рукописной подписи;
• биомеханические характеристики "клавиатурного почерка".
При регистрации пользователь должен продемонстрировать один или несколько раз свои характерные биометрические признаки. Эти признаки (известные как подлинные) регистрируются системой как контрольный "образ" законного пользователя. Этот образ пользователя хранится в электронной форме и используется для проверки идентичности каждого, кто выдает себя за соответствующего законного пользователя. В зависимости от совпадения или несовпадения совокупности предъявленных признаков с зарегистрированными в контрольном образе их предъявивший признается законным пользователем (при совпадении) или нет (при несовпадении).
Системы идентификации по узору радужной оболочки и сетчатки глаз могут быть разделены на два класса:
• использующие рисунок радужной оболочки глаза,
• использующие рисунок кровеносных сосудов сетчатки глаза.
Поскольку вероятность повторения данных параметров равна 10 , эти
системы являются наиболее надежными среди всех биометрических систем. Такие средства идентификации применяются там, где требуется высокий уровень безопасности (например, в США в зонах военных и оборонных объектов).
Системы идентификации по отпечаткам пальцев являются самыми распространенными. Одна из основных причин широкого распространения таких систем заключается в наличии больших банков данных по отпечаткам пальцев. Основными пользователями подобных систем во всем мире являются полиция, различные государственные и некоторые банковские организации.
Системы идентификации по геометрической форме руки используют сканеры формы руки, обычно устанавливаемые на стенах. Следует отметить,
что подавляющее большинство пользователей предпочитают системы именно этого типа, а не описанные выше.
Системы идентификации по лицу и голосу являются наиболее доступными из-за их дешевизны, поскольку большинство современных компьютеров имеют видео- и аудиосредства. Системы данного класса широко применяются при удаленной идентификации субъекта доступа в телекоммуникационных сетях.
Системы идентификации личностей по динамике рукописной подписи учитывают интенсивность каждого усилия подписывающего, частотные характеристики написания каждого элемента подписи и начертание подписи в целом.
Системы идентификации по биомеханическим характеристикам ”клавиатурного почерка” основываются на том, что моменты нажатия и отпускания клавиш при наборе текста на клавиатуре существенно различаются у разных пользователей. Этот динамический ритм набора ("клавиатурный почерк") позволяет построить достаточно надежные средства идентификации. В случае обнаружения изменения клавиатурного почерка пользователя ему автоматически запрещается работа на ЭВМ.
Следует отметить, что применение биометрических параметров при идентификации субъектов доступа автоматизированных систем пока не получило надлежащего нормативно-правового обеспечения, в частности в виде стандартов. Поэтому применение систем биометрической идентификации допускается только в автоматизированных системах, обрабатывающих и хранящих персональные данные, составляющие коммерческую и служебную тайну.
2.3. Взаимная проверка подлинности пользователей
Обычно стороны, вступающие в информационный обмен, нуждаются во взаимной проверке подлинности (аутентификации) друг друга. Этот процесс взаимной аутентификации выполняют в начале сеанса связи.
Для проверки подлинности применяют следующие способы:
• механизм запроса-ответа;
• механизм отметки времени ("временной штемпель").
Механизм запроса-ответа состоит в следующем. Если пользователь А хочет быть уверенным, что сообщения, получаемые им от пользователя В, не являются ложными, он включает в посылаемое для В сообщение непредсказуемый элемент-запрос X (например, некоторое случайное число). При ответе пользователь В должен выполнить над этим элементом некоторую операцию (например, вычислить некоторую функцию f(X)). Это невозможно осуществить заранее, так как пользователю В неизвестно, какое случайное число X придет в запросе. Получив ответ с результатом действий В, пользователь может быть уверен, что В - подлинный. Недостаток этого метода- возможность установления закономерности между запросом и ответом.
Механизм отметки времени подразумевает регистрацию времени для каждого сообщения. В этом случае каждый пользователь сети может определить, насколько "устарело" пришедшее сообщение, и решить не принимать его, поскольку оно может быть ложным.
В обоих случаях для защиты механизма контроля следует применять шифрование, чтобы быть уверенным, что ответ послан не злоумышленником.
При использовании отметок времени возникает проблема допустимого временного интервала задержки для подтверждения подлинности сеанса. Ведь сообщение с "временным штемпелем" в принципе не может быть передано мгновенно. Кроме того, компьютерные часы получателя и отправителя не могут быть абсолютно синхронизированы. Какое запаздывание "штемпеля" является подозрительным?
Для взаимной проверки подлинности обычно используют процедуру "рукопожатия”. Эта процедура базируется на указанных выше механизмах контроля и заключается во взаимной проверке ключей, используемых сторонами. Иначе говоря, стороны признают друг друга законными партнерами, если докажут друг другу, что обладают правильными ключами.
Процедуру рукопожатия обычно применяют в компьютерных сетях при организации сеанса связи между пользователями, пользователем и хост - компьютером, между хост - компьютерами и т.д.
Рассмотрим в качестве примера процедуру рукопожатия для двух пользователей А и В. (Это допущение не влияет на общность рассмотрения.
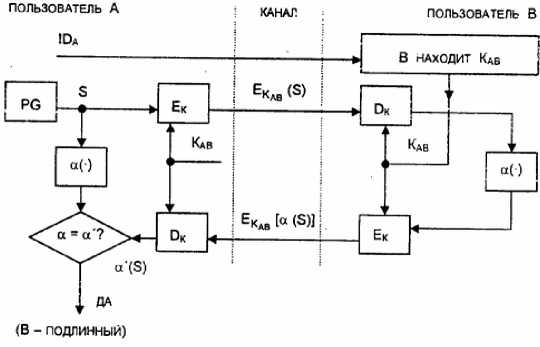 Рисунок 2.3 - Схема процедуры рукопожатия (пользователь А проверяет
подлинность пользователя В)
Рисунок 2.3 - Схема процедуры рукопожатия (пользователь А проверяет
подлинность пользователя В)
|
Такая же процедура используется, когда вступающие в связь стороны не являются пользователями). Пусть приценяется симметричная криптосистема. Пользователи А и В разделяют один и тот же секретный ключ КАВ. Вся процедура показана на рис. 2.3.
• Пусть пользователь А инициирует процедуру рукопожатия, отправляя пользователю В свой идентификатор IDA в открытой форме.
• Пользователь В, получив идентификатор IDA, находит в базе данных секретный ключ КАВ и вводит его в свою криптосистему.
• Тем временем пользователь А генерирует случайную последовательность S с помощью псевдослучайного генератора PG и отправляет ее пользователю В в виде криптограммы
Екав (S).
• Пользователь В расшифровывает эту криптограмму и раскрывает исходный вид последовательности S.
• Затем оба пользователя А и В преобразуют последовательность S, используя открытую одностороннюю функцию a(.).
• Пользователь В шифрует сообщение a(S) и отправляет эту криптограмму пользователю А.
• Наконец, пользователь А расшифровывает эту криптограмму и сравнивает полученное сообщение a'(S) с исходным a(S). Если эти сообщения равны, пользователь А признает подлинность пользователя В.
Очевидно, пользователь В проверяет подлинность пользователя А таким же способом. Обе эти процедуры образуют процедуру рукопожатия, которая обычно выполняется в самом начале любого сеанса связи между любыми двумя сторонами в компьютерных сетях.
Достоинством модели рукопожатия является то, что ни один из участников сеанса связи не получает никакой секретной информации во время процедуры подтверждения подлинности.
Иногда пользователи хотят иметь непрерывную проверку подлинности отправителей в течение всего сеанса связи. Один из простейших способов непрерывной проверки подлинности показан на рис. 5.4. Передаваемая криптограмма имеет вид
Ек(ГОа,М),
где ГОА-идентификатор отправителя А; М - сообщение.
Получатель В, принявший эту криптограмму, расшифровывает ее и раскрывает пару (IDA, M). Если принятый идентификатор IDA совпадает с хранимым значением IDA, получатель В признает эту криптограмму.
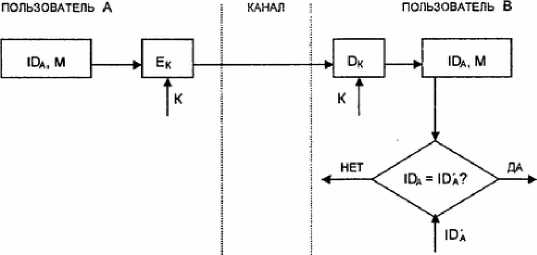 Рис. 5.4. Схема непрерывной проверки подлинности отправителя
Рисунок 2.4 - Схема непрерывной проверки подлинности отправителя
Рис. 5.4. Схема непрерывной проверки подлинности отправителя
Рисунок 2.4 - Схема непрерывной проверки подлинности отправителя
|
Другой вариант непрерывной проверки подлинности использует вместо идентификатора отправителя его секретный пароль. Заранее подготовленные пароли известны обеим сторонам. Пусть РА и Рв-пароли пользователей А и В соответственно. Тогда пользователь А создает криптограмму
С = Ек(Ра,М).
Получатель криптограммы расшифровывает ее и сравнивает пароль, извлеченный из этой криптограммы, с исходным значением. Если они равны, получатель признает эту криптограмму.
Процедура рукопожатия была рассмотрена в предположении, что пользователи А и В уже имеют общий секретный сеансовый ключ. Реальные процедуры предназначены для распределения ключей между подлинными партнерами и включает как этап распределения ключей, так и этап собственно подтверждения подлинности партнеров по информационному обмену.
2.4. Протоколы идентификации с нулевой передачей знаний
Широкое распространение интеллектуальных карт (смарт-карт) для разнообразных коммерческих, гражданских и военных применений (кредитные карты, карты социального страхования, карты доступа в охраняемое помещение, компьютерные пароли и ключи, и т.п.) потребовало обеспечения безопасной идентификации таких карт и их владельцев. Во многих приложениях главная проблема заключается в том, чтобы при предъявлении интеллектуальной карты оперативно обнаружить обман и отказать обманщику в допуске, ответе или обслуживании.
Для безопасного использования интеллектуальных карт разработаны протоколы идентификации с нулевой передачей знаний. Секретный ключ владельца карты становится неотъемлемым признаком его личности. Доказательство знания этого секретного ключа с нулевой передачей этого знания служит доказательством подлинности личности владельца карты.
Упрощенная схема идентификации с нулевой передачей знаний
Схему идентификации с нулевой передачей знаний предложили в 1986 г. У. Фейге, А. Фиат и А. Шамир. Она является наиболее известным доказательством идентичности с нулевой передачей конфиденциальной информации.
Рассмотрим сначала упрощенный вариант схемы идентификации с нулевой передачей знаний для более четкого выявления ее основной концепции. Прежде всего, выбирают случайное значение модуля n, который является произведением двух больших простых чисел. Модуль n должен иметь длину 512... 1024 бит. Это значение n может быть представлено группе пользователей, которым придется доказывать свою подлинность. В процессе идентификации участвуют две стороны:
• сторона А, доказывающая свою подлинность,
• сторона В, проверяющая представляемое стороной А доказательство.
Для того чтобы сгенерировать открытый и секретный ключи для стороны
А, доверенный арбитр (Центр) выбирает некоторое число V, которое является квадратичным вычетом по модулю п. Иначе говоря, выбирается такое число V, что сравнение
х2 =V(mod n)
имеет решение и существует целое число
V-1 mod n.
Выбранное значение V является открытым ключом для А. Затем вычисляют наименьшее значение S, для которого
S = sqrt(V-1)(modn).
Это значение S является секретным ключом для А.
Теперь можно приступить к выполнению протокола идентификации.
1. Сторона А выбирает некоторое случайное число r, r<n. Затем она вычисляет
х = r2 mod n
и отправляет х стороне В.
2. Сторона В посылает А случайный бит b.
3. Если b = 0, тогда А отправляет г стороне В. Если b = 1, то А отправляет стороне В
у = г * S mod n.
4. Если b = 0, сторона В проверяет, что
x = r2mod n,
чтобы убедиться, что А знает sqrt(x). Если b = 1, сторона В проверяет, что
x = y *Vmod n,
чтобы быть уверенной, что А знает sqrt(V1).
Эти шаги образуют один цикл протокола, называемый аккредитацией. Стороны А и В повторяют этот цикл t раз при разных случайных значениях r и b до тех пор, пока В не убедится, что А знает значение S.
Если сторона А не знает значения S, она может выбрать такое значение г, которое позволит ей обмануть сторону В, если В отправит ей b = 0, либо А может выбрать такое r, которое позволит обмануть В, если В отправит ей b = 1. Но этого невозможно сделать в обоих случаях. Вероятность того, что А обманет В в одном цикле, составляет 1/2. Вероятность обмануть В в t циклах равна (1/2)t
Для того чтобы этот протокол работал, сторона А никогда не должна повторно использовать значение г. Если А поступила бы таким образом, а сторона В отправила бы стороне А на шаге 2 другой случайный бит b, то В имела бы оба ответа А. После этого В может вычислить значение S, и для А все закончено.
Параллельная схема идентификации с нулевой передачей знаний
Параллельная схема идентификации позволяет увеличить число аккредитаций, выполняемых за один цикл, и тем самым уменьшить длительность процесса идентификации.
Как и в предыдущем случае, сначала генерируется число n как произведение двух больших чисел. Для того, чтобы сгенерировать открытый и секретный ключи для стороны А, сначала выбирают К различных чисел V1 V2, ...,Vk, где каждое V; является квадратичным вычетом по модулю n. Иначе говоря, выбирают значение Vi таким, что сравнение
х =Vi mod n
имеет решение и существует Vi-1modn. Полученная строка V1V2, ..., VK является открытым ключом.
Затем вычисляют такие наименьшие значения S,, что
Si = sqrt (Vi1) mod n.
Эта строка S1 S2,..., Sk является секретным ключом стороны А. Протокол процесса идентификации имеет следующий вид:
1. Сторона А выбирает некоторое случайное число r, r<n. Затем она вычисляет х = r mod n и посылает х стороне В.
2. Сторона В отправляет стороне А некоторую случайную двоичную строку из К бит: b1, b2,.... Ьк.
3. Сторона А вычисляет
у = r * (S1b1 * S2b2 *...* SKbk) mod n.
Перемножаются только те значения Si, для которых bi = 1. Например, если bi = 1, то сомножитель S1 входит в произведение, если же bi = 0, то S1 не входит в произведение, и т.д. Вычисленное значение у отправляется стороне В.
4. Сторона В проверяет, что
x = у2 * (V1b1 * V2b2 *...*Vkbk; mod n.
Фактически сторона В перемножает только те значения Vi, для которых bi = 1. Стороны А и В повторяют этот протокол t раз, пока В не убедится, что А знает S1, S2..................... Sk.
Вероятность того, что. А может обмануть В, равна (1/2)Kt. Авторы рекомендуют в качестве контрольного значения брать вероятность обмана В равной (1/2)20 при К = 5 и t=4.
Пример. Рассмотрим работу этого протокола для небольших числовых значений . Если n = 35 (n - произведение двух простых чисел 5 и 7), то возможные квадратичные вычеты будут следующими:
Таблица 2.3
| х2 = 1 (mod 35) | имеет решения: х = 1, 6. 29, 34; | |
| х2 = 4 (mod 35) | имеет решения: х = 2,12, 23, 33; | |
| х2 = 9 (mod 35) | имеет решения: х = 3, 17, 18, 32; | |
| х2 = 11 (mod 35) | имеет решения: х = 9, 16.19, 26; | |
| х2 = 14 (mod 35) | имеет решения: х = 7, 28; | |
| х2 =15 (mod 35) | имеет решения: х = 15, 20; | |
| x2* 16 (mod 35) | имеет решения: х = 4, 11, 24, 31; | |
| x2 =21 (mod 35) | имеет решения: х = 14, 21; | |
| x2 = 25 (mod 35) | имеет решения: х = 5, 30; | |
| x2 =29 (mod 35) | имеет решения: х = 8, 13, 22, 27; | |
| x2 = 30 (mod 35) | имеет решения: х - 10, 25. |
Заметим, что 14, 15, 21, 25 и 30 не имеют обратных значений по модулю 35. потому что они не являются взаимно простыми с 35. Следует также отметить, что число квадратичных вычетов по модулю 35, взаимно простых с n = p*q = 5*7=35 (для которых НОД (х, 35) = 1), равно
(р -1) (q -1)/4 = (5 -1) (7-1)/4 = 6.
Составим таблицу квадратичных вычетов по модулю 35, обратных к ним значений по модулю 35 и их квадратных корней.
Таблица 2.4
| V | V-1 | S = sqrt(V-1') |
| Итак, сторона А получает открытый ключ, состоящий из К=4 значений V: |
[4, 11, 16, 29]. Соответствующий секретный ключ, состоящий из К=4 значений S:
[3 4 9 8].
Рассмотрим один цикл протокола.
1. Сторона А выбирает некоторое случайное число г =16, вычисляет
x=162 mod35=11
и посылает это значение х стороне В.
2. Сторона В отправляет стороне А некоторую случайную двоичную строку
[1, 1,0, 1].
3. Сторона А вычисляет значение
у = r * (S1b1 * S2b2 *...* SKbk) mod n =16 * (З1 * 41 * 9° * 81) mod 35 = 31
и отправляет это значение у стороне В.
4. Сторона В проверяет, что
x = у2 * (V1b1 * V2b2 *...*Vkbkj mod n = 312 * (41 *111 *16° * 291) mod 35 =11.
Стороны А и В повторяют этот протокол t раз, каждый раз с разным случайным числом r, пока сторона В не будет удовлетворена.
При малых значениях величин, как в данном примере, не достигается настоящей безопасности. Но если n представляет собой число длиной 512 бит и более, сторона В не сможет узнать ничего о секретном ключе стороны А, кроме того факта, что сторона А знает этот ключ.
В этот протокол можно включить идентификационную информацию.
Пусть I-некоторая двоичная строка, представляющая иден
тификационную информацию о владельце карты (имя, адрес, персональный идентификационный номер, физическое описание) и о карте (дата окончания действия и т.п.). Эту информацию I формируют в Центре выдачи интеллектуальных карт по заявке пользователя А.
Далее используют одностороннюю функцию f() для вычисления f(i,j), где j-некоторое двоичное число, сцепляемое со строкой i. Вычисляют значения
Vj = f(l, j)
для небольших значений j, отбирают К разных значений j, для которых Vj являются квадратичными вычетами по модулю п. Затем для отобранных квадратичных вычетов Vj вычисляют наименьшие квадратные корни из Vj" 1(mod n). Совокупность из К значений Vj образует открытый ключ, а совокупность из К значений Sj-секретный ключ пользователя А.
2.5 Схема идентификации Гиллоу-Куискуотера
Алгоритм идентификации с нулевой передачей знания, разработанный Л. Гиллоу и Ж. Куискуотером, имеет несколько лучшие характеристики, чем предыдущая схема идентификации. В этом алгоритме обмены между сторонами А и В и аккредитации в каждом обмене доведены до абсолютного минимума для каждого доказательства требуется только один обмен с одной аккредитацией. Однако объем требуемых вычислений для этого алгоритма больше, чем для схемы Фейге-Фиата-Шамира.
Пусть сторона А-интеллектуальная карточка, которая должна доказать свою подлинность проверяющей стороне В. Идентификационная информация стороны А представляет собой битовую строку I, которая включает имя владельца карточки, срок действия, номер банковского счета и др. Фактически идентификационные данные могут занимать достаточно длинную строку, и тогда их хэшируют к значению I.
Строка I является аналогом открытого ключа. Другой открытой информацией, которую используют все карты, участвующие в данном приложении, являются модуль п и показатель степени V Модуль п является произведением двух секретных простых чисел.
Секретным ключом стороны А является величина G, выбираемая таким образом, чтобы выполнялось соотношение
l*Gv=1(modn)
Сторона А отправляет стороне В свои идентификационные данные I. Далее ей нужно доказать стороне В, что эти идентификационные данные принадлежат именно ей. Чтобы добиться этого, сторона А должна убедить сторону В, что ей известно значение G.
Вот протокол доказательства подлинности А без передачи стороне В значения G:
1. Сторона А выбирает случайное целое г, такое, что 1<г<п-1. Она вычисляет
T=rvmodn
и отправляет это значение стороне В.
2. Сторона В выбирает случайное целое d, такое, что 1<d<n-1, и отправляет это значение d стороне А.
3. Сторона А вычисляет
D = r * Gd mod n
и отправляет это значение стороне В.
4. Сторона В вычисляет значение
Т'= DvIdmod n.
Если T=T'(mod n),
то проверка подлинности успешно завершена.
Математические выкладки, использованные в этом протоколе, не очень сложны:
Т'= DvId = (rGd)v ld = rvGdvId = rv(IGv)d = rv=T(mod n), поскольку G вычислялось таким образом, чтобы выполнялось соотношение
IGv=1(modn).
2.6 Контрольные вопросы
1. Каковы процедуры инициализации объекта информационной защиты?
2. Опишите типовые схемы идентификации и аутентификации пользователя.
3. Каковы недостатки и достоинства схемы простой аутентификации с помощью пароля?
4. Достоинства биометрических методов идентификации и аутентификации пользователя по сравнению с традиционными?
3. СРЕДСТВА И МЕТОДЫ ОГРАНИЧЕНИЯ ДОСТУПА К
ФАЙЛАМ
3.1 Защита информации в КС от несанкционированного доступа
Для осуществления НСДИ злоумышленник не применяет никаких аппаратных или программных средств, не входящих в состав КС. Он осуществляет НСДИ, используя:
• знания о КС и умения работать с ней;
• сведения о системе защиты информации;
• сбои, отказы технических и программных средств;
• ошибки, небрежность обслуживающего персонала и пользователей.
Дата добавления: 2016-02-16; просмотров: 1818;
