Теоретические основы вычислительной техники 4 страница
1. Перейти от МДНФ к МКНФ при помощи правила Де Моргана.
2. Использовать клетки КК содержащие нули.
| х3х4 | |||||
| х1х2 | | | |||
| | | ||||
| группа 1 | |||||
| группа 2 | |||||
| группа 3 | |||||
| группа 4 |
Составление МКНФ заключается в объединении конъюнкциями дизъюнкций, соответствующих всем выделенным группам. В дизъюнкцию включаются все переменные, значения которых не изменяются в пределах группы. Причём, если переменная в пределах группы равна 0, то она входит в дизъюнкцию без инверсии, а если равна 1, то с инверсией.
Пример. Дана карта Карно для функции 4-х переменных. Получить МКНФ этой функции.
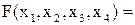
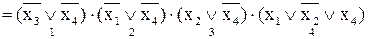
Задание 60. Получить МКНФ для функции F4 заданной в таблице 4.
Задание 61. Получить МКНФ для функции F3 заданной в таблице 4.
В. Минимизация неполностью определённых функций.
Неполностью определённые функции это такие функции, которые определены не на всех 2n наборах аргументов.
На карте Карно неопределённое условие обозначается прочерком (-). Клетки с прочерком могут произвольным образом включаться в группы, как при построении МДНФ, так и при построении МКНФ. Более того, их можно вообще никуда не включать (игнорировать).
Пример. Дана карта Карно для функции 4-х переменных. Получить МДНФ и МКНФ этой функции.
| х3х4 | |||||
| х1х2 | - | - | |||
| - | |||||
| - | - | - | |||
| группа 1 | |||||
| группа 2 | |||||
| группа 1 | |||||
| группа 2 |
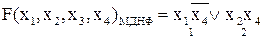
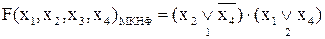
Задание 62. Получить МДНФ для функции F5 заданной в таблице 4.
Задание 63. Получить МДНФ и МКНФ для функции F6 заданной в таблице 4.
Минимизация методом Морреля.
В основе метода лежит теорема разложения.
Теорема разложения. Любую логическую функцию от n переменных можно свести к двум функциям от (n-1) переменных, проведя разложение вида
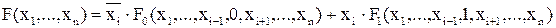
Сущность метода заключается в последовательном разложении функции по переменным и в анализе остаточных функций на равенство их нулю или единице.
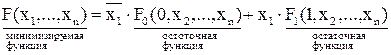
Если остаточная функция равна нулю, то член, её включающий, равен нулю и исключается из разложения. Если остаточная функция равна единице, то переменная или конъюнкция переменных, связанных с ней, входит в тупиковую форму, а член из дальнейшего рассмотрения исключается. Все оставшиеся после анализа остаточные функции разлагаются по следующей переменной и снова анализируются и т. д. Минимизация заканчивается когда все остаточные функции будут равны 0 или 1.
Для получения формы, наиболее близкой к минимальной, Моррель предложил в формулу разложения добавить так называемый «терм Морреля», который добавляется всякий раз при разложении по любой переменной.
Формула разложения примет вид: 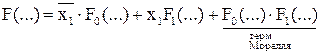
Покажем, что терм Морелля не изменит функцию:
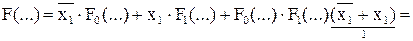
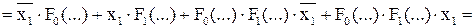
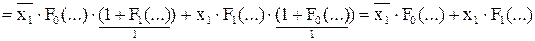 .
.
При анализе остаточных функций на каждом этапе разложения проверяются условия поглощения термом Морреля других остаточных функций.
Минимизацию методом Морреля удобно проводить над функцией представленной в строчной форме (т. к. метод реализуем на ЭВМ). Разложение функции, представленной в строчной форме, по переменной хi означает её разбиение на две части. В первую часть входят те наборы, на которых хi=0, а во вторую – на которых хi=1.
Пример. Пусть задана функция F(A,B,C,D) в строчной форме.
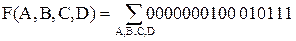 . Выполнить разложение функции по переменной А.
. Выполнить разложение функции по переменной А.
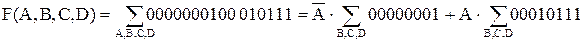 .
.
Теперь получим терм Морреля и добавим в разложение.
| получение терма Морреля поразрядным умножением | ||
| -терм Морреля |
Следовательно, 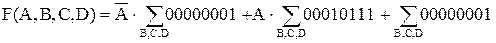
Пример. Минимизировать методом Морреля функцию
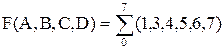 .
.
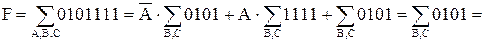
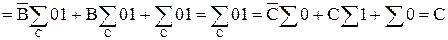
Таким образом, получим F(A,B,C,D)=A+C.
Задание 64. Выполнить разложение функции F1 (таблица 3) по переменной х1.
Задание 65. Минимизировать функцию F2 (таблица 3) методом Морелля.
Задание 66. Минимизировать функцию  методом Морреля.
методом Морреля.
1.4. Синтез и анализ комбинационных схем.
Устройство, осуществляющее дискретное преобразование информации ЭВМ, называется автоматом. Существуют два основных вида дискретных автоматов: комбинационные автоматы (схемы) и конечные автоматы.
Введём: Х(t)={x1, x2, …, xi, …, xn} – множество входных дискретных сигналов; 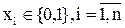 .
.
Y(t)={y1, y2, …, yj, …, ym} – множество выходных дискретных сигналов; 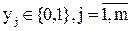 .
.
Здесь t – дискретное время, определяется моментами перехода автомата из одного состояния в другое.
 |

Определение. Если совокупность выходных сигналов (выходного слова) Y(t) зависит только от совокупности входных сигналов (входного слова) X(t) и не зависит от внутренних состояний автомата, то такой автомат называется комбинационным автоматом (комбинационной схемой).
Структурная схема комбинационного автомата:
 |
Здесь Р – функция преобразования.
Закон функционирования комбинационной схемы определяется заданием соответствия между её входными и выходными словами Y(t)=P[X(t)] и может быть дан таблицей истинности, в аналитический форме и др.
1.4.1. Алгоритм синтеза комбинационной схемы.
1. Задать закон функционирования комбинационной схемы.
2. Провести минимизацию функции преобразования Р, получить РМДНФ и РМКНФ.
3. Преобразовать РМДНФ и РМКНФ в соответствии с заданным базисом логических функций (используемыми логическими элементами) и выбрать наиболее компактную форму представления Р.
4. Построить функциональную схему устройства.
5. Выполнить схемотехническую коррекцию схемы с учётом характеристик и параметров используемых логических элементов:
- коэффициента объединения (количество входов элемента),
- коэффициента разветвления (характеризует нагрузочную способность – максимально допустимое количество элементов подключаемых к входу),
- уровня логических 0 и 1,
- помехозащитности и др.
6. Провести тестирование полученной схемы на соответствие закону функционирования. Этот этап является уже частью анализа схемы и ставит задачей убедится в её работоспособности.
1.4.2. Функциональные схемы логических элементов.
Приведём лишь функциональные схемы, реализующие простейшие логические функции.
дизъюнкция («или»)
 |
конъюнкция («и»)
 |
инверсия («не»)
 |
(здесь и в дальнейшем будет употребляться закрашенный кружок в обозначении инверсии вместо не закрашенного как принято)
стрелка Пирса («или-не»)
 |
штрих Шеффера («и-не»)
 |
Свести 3-х и 4-х входовые логические схемы к 2-х входовым можно следующим образом:
«3 и»
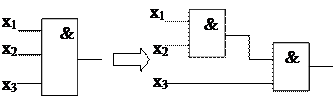 |
«3 или»
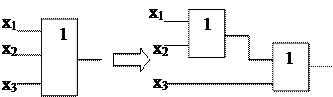 |
«4 и»
 |
«4 или»
 |
«3 и-не»
 |
«3 или-не»
 |
 «4 и-не»
«4 и-не»
«4 или-не»

1.4.3. Пример синтеза полного одноразрядного двоичного сумматора.
Пример. Синтезировать схему полного одноразрядного двоичного сумматора используя двухвходовые логические элементы, реализующие логическую функцию «и-не».
Представим сумматор в виде:
 |
a и b – одноразрядные двоичные слагаемые.,
с – перенос из младшего разряда,
S – сумма,
Р – перенос в старший разряд.
S=F1(a,b,c), P=F2(a,b,c).
При синтезе реализуем последовательно этапы алгоритма.
1. Зададим закон функционирования сумматора в виде ТИ.
| с | b | a | S | P |
2. Проведём минимизацию функций S и Р методом Карно. По ТИ составим карты Карно:
| ab | |||||
| с | |||||
| для S |
| ab | |||||
| с | |||||
| для P |
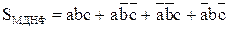
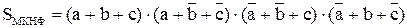
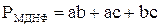
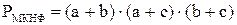
 Проверим предварительное построение схем сумматора непосредственно по выражениям SМДНФ и РМДНФ без преобразования их к заданным двухвходовым элементам «и-не».
Проверим предварительное построение схем сумматора непосредственно по выражениям SМДНФ и РМДНФ без преобразования их к заданным двухвходовым элементам «и-не».
3. Преобразуем полученные выражения в соответствии с задуманными логическими элементами «и-не».
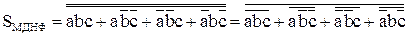
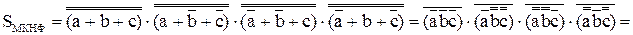
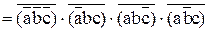 .
.
Для построения SМДНФ и SМКНФ на двухвходовых элементах «и-не» потребуется соответственно 20 и 21 логический элемент. Поэтому для построения части схемы, реализующей S, выберем SМДНФ.
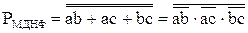 ,
,
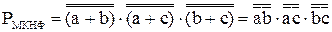 .
.
Для реализации PМДНФ необходимо 6 двухвходовых элементов «и-не», а для РМКНФ – 7 (с учётом того, что 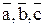 уже получены в SМДНФ).
уже получены в SМДНФ).
Для построения части схемы, реализующей Р, выберем РМДНФ.
4. Построим функциональную схему сумматора используя выражения, выбранные на третьем шаге алгоритма.
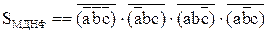 ;
; 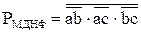 .
.
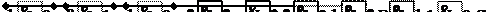
В данном случае построение частей схемы, реализующих S и Р проводилось независимо друг от друга.
5. На этапе схемотехнической коррекции ограничимся лишь оценкой выполнения требований по коэффициентам объединения Ко и разветвления Кр. К0 был задан равным двум, а Кр для логических схем равен 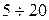 . Зададим Кр=5. Схема показывает, что для всех элементов К0=2, а Кр<4 и, следовательно, требования по Ко и Кр удовлетворены.
. Зададим Кр=5. Схема показывает, что для всех элементов К0=2, а Кр<4 и, следовательно, требования по Ко и Кр удовлетворены.
6. Проведём тестирование схемы сумматора только на одном наборе аргументов. Пусть а=1, b=0, c=1. По ТИ этому набору соответствуют S=0 и Р=1. Расположим на всех входах и выходах элементов схемы соответствующие логические значения (0 или 1) и убедимся в правильности реализации функции S и Р на данном наборе аргументов (см. схему). Если выполнить аналогичные действия для всех наборов аргументов их ТИ, то тестирование будет полным.
Обратим внимание на то, что полученная схема, в соответствии с заданием, содержит только двухвходовые элементы «и-не».
| таблица 5 | ||||||
| х1 | х2 | х3 | х4 | F1 | F2 | F3 |
| - - - |
Задание 67. Синтезировать комбинационную схему, закон функционирования которой задан функцией F4 (таблица 4), используя логические элементы «и-не».
Задание 68. Синтезировать комбинационную схему полного одноразрядного сумматора на двухвходовых логических элементах «или-не» и протестировать её на наборе a=1, b=1, c=0.
Задание 69. Синтезировать комбинационную схему, реализующую функцию F1, заданную в таблице 5. Использовать двухвходовые логические элементы «или-не». Провести тестирование схемы при х1=0, х2=1, х3=1, х4=0.
| таблица 6 | |||||
| х1 | х2 | х3 | F1 | F2 | F3 |
| - - |
Задание 70. Синтезировать комбинационную схему, реализующую функции F2 и F5, заданные в таблицах 5 и 6. Использовать двухвходовые логические элементы «и-не». Провести тестирование схем при х1=0, х2=1, х3=1, х4=1.
Задание 71. Синтезировать комбинационную схему, реализующую функции F3 и F6, заданные в таблицах 5 и 6. Использовать логические элементы: «не» и «2и». Провести тестирование при х1=х3=х5=0, х2=х4=1.
1.4.4. Односторонние булевы уравнения
Рассмотрим метод решения односторонних булевых уравнений с одним и двумя неизвестными. Уравнения с одним неизвестным:
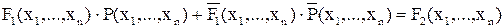 .
.
Уравнения с двумя неизвестными:
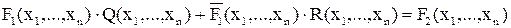 ,
,
где F1(…) и F2(…) – известные (заданные) функции, а Р(…), Q(…), R(…) – неизвестные функции.
Решение этих уравнений будем искать методом подбора значений P, Q, R на всех наборах F1 и F2. Таких наборов 4. Составим таблицу решений.
| таб. решений | ||||
| F1 | F2 | P | Q | R |
| - - | - - |
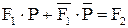 ;
; 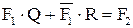 .
.
Для получения решений в виде 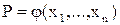 для уравнений с одним неизвестным и
для уравнений с одним неизвестным и 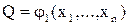 ,
, 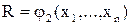 для уравнения с двумя неизвестными, необходимо сначала перейти от формы представления исходных функций F1 и F2 к форме представления функций P, Q, R (для этого используется таблица решений), а затем выполнить минимизацию этих функций.
для уравнения с двумя неизвестными, необходимо сначала перейти от формы представления исходных функций F1 и F2 к форме представления функций P, Q, R (для этого используется таблица решений), а затем выполнить минимизацию этих функций.
Пример. Решить булевы уравнения 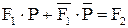 и
и 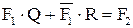 при F1 и F2 заданных в строчной форме:
при F1 и F2 заданных в строчной форме: 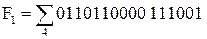 ,
, 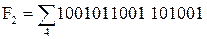 . Выполнить переход от F1 и F2 к P, Q, R. Используем таблицу решений односторонних булевых уравнений.
. Выполнить переход от F1 и F2 к P, Q, R. Используем таблицу решений односторонних булевых уравнений.
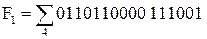
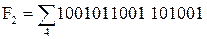
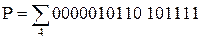
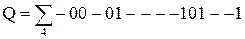
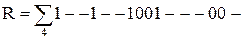
Перейдём от представления P, Q и R к строчной форме к представлению картами Карно и выполним минимизацию:
| карта Карно для Р | |||||
| x3x4 | |||||
| X1x2 | |||||
| Карта Карно для R | |||||
| x3x4 | |||||
| x1x2 | - | - | |||
| - | - | ||||
| - | - | ||||
| - | - |
| карта Карно для Q | |||||
| x3x4 | |||||
| x1x2 | - | - | |||
| - | - | ||||
| - | - | ||||
| - | - |
Проведя минимизацию Р, Q и R получим:
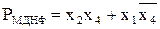 ,
, 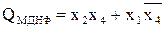 ,
, 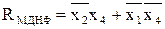 .
.
Задание 72. Решить односторонние булевы уравнения с одним и двумя неизвестными, если известные функции F4 и F5 заданы ТИ (таблица 6).
Задание 73. Решить односторонние булевы уравнения с одним и двумя неизвестными, если известные функции F1 и F2 заданы ТИ (таблица 5).
1.4.5. Методы синтеза комбинационных схем с многими выходами.
Послу раздельной минимизации булевых функций, описывающих многовыходную схему, применяются различные методы совместной обработки функций.
Рассмотрим два из них:
- метод учёта повторяющихся членов,
- метод последовательного наращивания.
Метод учёта повторяющихся членов.
В данном методе находятся общие для формул нескольких функций члены(функции, отдельные дизъюнкции, конъюнкции и их части). При построении общей комбинационной схемы, реализующей несколько логических функций, фрагменты, соответствующие общим (повторяющимся) членам, формируются только один раз и используются для получения любой функции, куда они входят.
Пример. Синтезировать комбинационную схему, реализующую функции:
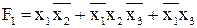 ,
, 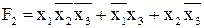 ,
, 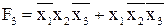 .
.
Общими членами в этих выражениях являются: 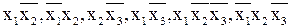 .
.

Задание 74. Синтезировать комбинационную схему, реализующую функции:

Метод последовательного наращивания.
 Логическая схема строится сначала для какого-либо одного выхода, затем для другого, третьего и т. д.
Логическая схема строится сначала для какого-либо одного выхода, затем для другого, третьего и т. д.
При построении схемы последующего выхода, выходные сигналы уже построенной схемы используются на ряду с общими выходными сигналами схемы. Следовательно, функция этого выхода может быть представлена в виде функции от (n+1) переменной (n – входных сигналов плюс выход предыдущей схемы).
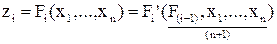
Реализуя данный метод нужно получить специальный блок, преобразующий функцию Fi-1 в функцию Fi. Для этого проведём разложение Fi по новой перемноженной Fi’: 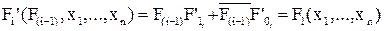 .
.
Таким образом, получаем обычное булево уравнение с двумя неизвестными 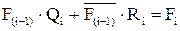 . Следовательно, при построении многовыходной схемы методом последовательного наращивания необходимо найти решение (n-1) булева уравнения и определить все Qi и Ri.
. Следовательно, при построении многовыходной схемы методом последовательного наращивания необходимо найти решение (n-1) булева уравнения и определить все Qi и Ri.
Рекомендации. За исходную функцию F1 можно брать любую из заданных, но, как правило, лучшие результаты получаются, если взять ту, у которой проще минимальная форма.
Если одна из исходных функций не доопределена, а вторая определена полностью, то неопределённые значения группируются так, чтобы это было наиболее выгодно при минимализации Qi и Ri.
Структурная схема, реализующая функцию F’i может быть представлена следующим образом:
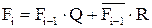 .
. 
Пример. Синтезировать комбинационную схему полного одноразрядного двоичного сумматора методом последовательного наращивания. 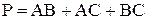 ,
, 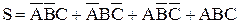 . В качестве F1 выбираем Р, как функцию с простой минимальной формой.
. В качестве F1 выбираем Р, как функцию с простой минимальной формой. 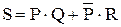 .
.
Дата добавления: 2016-04-06; просмотров: 845;
