Теоретические основы вычислительной техники 5 страница
| AB | |||||
| C | |||||
| для Р |
| AB | |||||
| C | |||||
| для S |
| AB | |||||
| C | - | - | - | ||
| - | |||||
| для Q |
| AB | |||||
| C | - | ||||
| - | - | - | |||
| для R | |||||
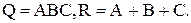
Проведём тестирование построенной схемы на наборе аргументов А=1, В=0, С=1. Этому набору должны соответствовать значения S=0 и Р=1. Проставленные логические значения на входах и выходах элементов схемы показывают работоспособность схемы (на данном наборе).
 При синтезе многовыходных схем методом последовательного наращивания удаётся, обычно, построить схему с использованием меньшего количества логических элементов, чем при синтезе с независимым построением частей схемы, реализующих функции выходов. Но при этом получается некоторый проигрыш в быстродействии схемы.
При синтезе многовыходных схем методом последовательного наращивания удаётся, обычно, построить схему с использованием меньшего количества логических элементов, чем при синтезе с независимым построением частей схемы, реализующих функции выходов. Но при этом получается некоторый проигрыш в быстродействии схемы.
Задание 75. Реализовать рассмотренную схему только на двухвходовых элементах «и-не» и, проведя сравнение полученной реализации со схемой, определить выигрыш (проигрыш) в количестве элементов схемы и её быстродействии.
Задание 76. Используя условия задания 70 синтезировать двухвыходную комбинационную схему методом последовательного наращивания.
Задание 77 Используя условия задания 71 синтезировать двухвыходную комбинационную схему методом последовательного наращивания.
1.5. Синтез и анализ конечных автоматов.
Определение. Если совокупность выходных сигналов (выходного слова) Y(t) зависит, как от совокупности входных сигналов (входного слова) X(t), так и от внутренних состояний S(t-1), то такой преобразователь информации называется конечным автоматом (автоматом с памятью).
Для описания функционирования конечного автомата (КА) задаются:
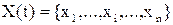 - множество входных дискретных сигналов,
- множество входных дискретных сигналов, 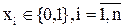 ;
;
Y(t)={y1,…,yj,…,ym} – множество выходных дискретных сигналов, 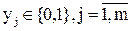 ;
;
S(t)={s1,…,sk,…sr} – множество внутренних дискретных состояний, 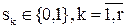 ;
;
s0 – начальное состояние автомата;
FP – функция переходов, позволяющая определить новое внутреннее состояние автомата, если известно предыдущее внутреннее состояние и состояние входных сигналов в данных момент времени S(t+1)=FP[S(t),X(t)];
FV – функция выходов, позволяющая определить состояние выходных сигналов автомата, если известно внутреннее состояние и состояние входных сигналов Y(t)=FV[S(t),X(t)].
Таким образом, функционирования КА можно представить так:
 S(t+1)=FP[S(t),X(t)],
S(t+1)=FP[S(t),X(t)],
Y(t)=FV[S(t),X(t)], где t=0,1,2…
S(t=0)=s0
Автомат Мили
или так:
 S(t+1)=FP[S(t),X(t)],
S(t+1)=FP[S(t),X(t)],
Y(t)=FV[S(t)], где t=0,1,2…
S(t=0)=s0
Автомат Мура
Конечные автоматы делятся на 2 части:
Абстрактную – описание полноты FV, X, Y, S автомата, работоспособности
Структурную – отвечает на вопрос как построить КА.
При описании работы конечного автомата используют таблицы состояний или графы (диаграммы состояний).
таблицы состояний:
| таблица переходов | ||||
| s0 | s1 | … | sr | |
| x1 x2 … xn | s3 s1 ... … | s0 s3 … … | … … … … | … … … … |
| таблица выходов | ||||
| s0 | s1 | … | sr | |
| x1 x2 … xn | y4 y1 ... … | y2 y3 … … | … … … … | … … … … |
| совмещённая таблица | |||
| s0(t) | s1(t) | … | |
| x1(t) | 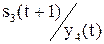
| 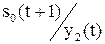
| … |
| x2(t) | 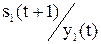
| 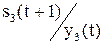
| … |
| … | … | … | … |
| (фрагмент) |
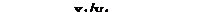
Задание КА графом (соответствует содержимому таблиц состояний).
Различают два основных типа КА: автомат Мили м автомат Мура. Различие между ними заключается в том, что в автомате Мура состояние выходных сигналов не зависит от состояния входных сигналов, а определяется лишь внутренним состоянием, т. е. Y(t)=FV[S(t)].
Структурная схема КА.
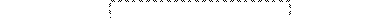
или несколько подробнее

КС – комбинационная схема,
БП – блок памяти,
БФВС – блок формирования выходных сигналов (комбинационная схема, реализующая FV),
БВЭА – блок возбуждения элементарных автоматов (комбинационная схема, реализующая FP),
БЭА – блок элементарных автоматов (память КА),
q – функция возбуждения.
1.5.1. Элементарные конечные автоматы и их техническая реализация.
Функция памяти КА реализуется на элементарных автоматах. Элементарный автомат (ЭА) – это автомат Мура, имеющий два и только два различных состояния, имеющий 1 или 2 входа, при подаче сигналов на которые возможен переход из одного состояния в другое.
| q(t) | 0 0 1 1 |
| Q(t) | 0 1 0 1 |
| Q1(t+1) | 0 0 1 1 |
| Q2(t+1) | 0 1 1 0 |
Для построения памяти КА используются, в основном, четыре типа ЭА: два типа одновходовых и два двухвходовых.
Одновходовые ЭА:
Q1(t+1)=q(t) – ЭА D-типа,
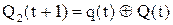 - ЭА T-типа.
- ЭА T-типа.
| q0(t) | 0 0 0 0 1 1 1 1 |
| q1(t) | 0 0 1 1 0 0 1 1 |
| Q(t) | 0 1 0 1 0 1 0 1 |
| Q3(t+1) | 0 1 1 1 0 0 - - |
| Q4(t+1) | 0 1 1 1 0 0 1 0 |
Двухвходовые ЭА:
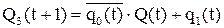 - ЭА RS-типа,
- ЭА RS-типа,
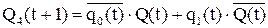 - ЭА JK-типа.
- ЭА JK-типа.
Техническая реализация ЭА:
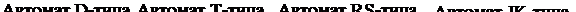
q1(t)=qS(t), q1(t)=qJ(t), q0(t)=qR(t), q0(t)=qK(t).
1.5.2. Алгоритм структурного синтеза конечного автомата.
1. Задать закон функционирования конечного автомата.
2. Определить n – требуемое количество ЭА. n=ù log2(r+1) é , где r+1 – количество внутренних состояний ЭА, ù … é - ближайшее большее целое.
| тип ЭА | |||||
| D | T | RS | JK | |||
| qD(t) | qT(t) | qS(t) | qR(t) | qJ(t) | qK(t) | |
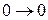
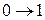
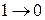
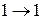
| - | - | - - | - - |
3. Выбрать тип ЭА по таблице. Для этого предварительно построить таблицу для требуемой функции возбуждения.
4. Построить функциональную схему БЭА.
5. Провести синтез комбинационной схемы БВЭА.
6. Провести синтез комбинационной схемы БФВС.
7. Составить из БЭА, БВЭА и БФВС схему конечного автомата.
8. Провести тестирование полученной схемы на соответствие закону функционирования.
1.5.3. Пример синтеза конечного автомата – двоично-десятичного счётчика.
Пример. Синтезировать схему двоично-десятичного счётчика.
| Q0 | ||||||||||
| Q1 | ||||||||||
| Q2 | ||||||||||
| Q3 |
Зададим закон функционирования двоично-десятичного счётчика. Этот КА имеет 10 внутренних состояний:

Так как n=ù log210 é=4, то для запоминания всех 10 состояний КА потребуется четыре ЭА.
Выберем Тим ЭА. Пусть это будет ЭА Т-типа. Тогда структурная схема синтезируемого КА будет иметь вид:

Выполним синтез БВЭА. Построим либо совмещённую таблицу состояний, либо диаграмму состояний:
| Таблица состояний | |||||||||||||
| текущее состояние | следующее состояние | выходы комбинационной схемы | |||||||||||
| Q3 | Q2 | Q1 | Q0 | Q3 | Q2 | Q1 | Q0 | q3 | q2 | q1 | q0 | / | c |
| / / / / / / / / / / |
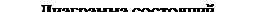 Над дробью в диаграмме ничего нет, т. к. входные сигналы отсутствуют в данной схеме. Под дробью значение выхода С.
Над дробью в диаграмме ничего нет, т. к. входные сигналы отсутствуют в данной схеме. Под дробью значение выхода С.
Построим карты Карно для выходных сигналов БВЭА (т. е. для сигналов q0, q1, q2, q3).
| KK для q3 | |||||
| Q1Q0 | |||||
| Q3Q2 | |||||
| - | - | - | - | ||
| - | - |
| KK для q2 | |||||
| Q1Q0 | |||||
| Q3Q2 | |||||
| - | - | - | - | ||
| - | - |
| KK для q1 | |||||
| Q1Q0 | |||||
| Q3Q2 | |||||
| - | - | - | - | ||
| - | - |
| KK для q0 | |||||
| Q1Q0 | |||||
| Q3Q2 | |||||
| - | - | - | - | ||
| - | - |
Проведём синтез БФВС. Построим карту Карно для выходных сигналов комбинационной схемы БФВС. (т. е. для сигнала С).
| KK для С | |||||
| Q1Q0 | |||||
| Q3Q2 | |||||
| - | - | - | - | ||
| - | - |
С=Q3Q0.
Составим из БЭА, БВЭА и БФВС схему конечного автомата:
Вспомним соответствие с общей структурой КА:

Проверим работоспособность схемы на примере перехода из состояния 9 в 0 и формирования С. В этом состоянии Q3=1, Q2=0, Q1=0, Q0=1 (см. 1 и 0 в схеме). При этом сформируются сигналы возбуждения: q3=1, q2=0, q1=0, q0=1 и, следовательно, следующим состоянием КА будет: Q3=Q2=Q1=Q0=0 и С=1, что соответствует правильной работе двоично-десятичного счётчика.
Задание 78. Синтезировать схему КА, который, при подаче на вход счётных импульсов, переходит последовательно в состояния  в соответствии с рисунком.
в соответствии с рисунком.

Задание 79. Синтезировать схему КА, который на входные счётные импульсы последовательно формирует на выходах двоичные коды, соответствующие числам 0, 2, 4, 5, 7, 9. В качестве ЭА выбрать Т-триггеры.
Задание 80. Синтезировать схему КА в соответствии с заданием №79, но с использованием в качестве ЭА RS-триггеров.
2. Организация ЭВМ.
2.1. Типовые структурные элементы цифровой техники.
2.1.1. Основные характеристики и классификация цифровых элементов вычислительной техники.
Типовыми структурными элементами называются наименьшие функциональные части из которых состоят устройства цифровой техники.
Это:
- элементы реализующие логические функции,
- элементы преобразующие информацию,
- элементы запоминающие информацию,
- вспомогательные элементы (генерирующие, формирующие и усиливающие сигналы).
По способу представления информации структурные элементы делятся на:
- импульсные («0» - отсутствие импульса напряжения, «1» - наличие импульса напряжения)
- потенциальные («0» - один уровень напряжения, «1» - другой уровень напряжения)
Условные обозначения схем.
0123456 – номера элементов обозначения
0 – буква «К» или « »
1+2 – обозначение серии
3 – буква, указывающая на функциональный класс
4 – буква, указывающая на группу данного функционального класса
5 – число, указывающее номер разработки данной микросхемы в серии
6 – буква, цветная точка или др. – маркировка по разбросу параметров, предельным эксплутационным режимам и другим признакам, вызванным отклонением технологического процесса.
Микросхема дана в технических условиях на серию.
К – широкое потребление
серия – ряд функционально различных микросхем объединённых по технологии, параметрам, конструктивному оформлению.
Обозначение серии:
1 элемент – цифра, указывающая на технологический признак
1, 5, 7 – полупроводниковые микросхемы
2, 4, 6 – гибридные микросхемы
3 – плёночные микросхемы
 например:
например:
К155ЛАЗ
2.1.2. Мультиплексоры и дешифраторы.
I. Мультиплексор – схема, передающая сигналы с одной из нескольких входных линий в выходную линию

При подаче на управляющие входы двоичного кода и на вход W нуля, к выходу подключается только тот вход, номер которого в десятичном изображении совпадает со значением двоичного кода на управляющих входах. Информация на других информационных входах не влияет.
Реализация логических функций на мультиплексорах. (любых КС).
Пусть задана функция трёх переменных на мультиплексорах. Составим ТИ.
| х1 | х2 | х3 | y |
| … | … | … | f(0,0,0) f(1,0,0) … f(1,1,1) |

Для функции 4-х переменных:
| х1 | х2 | х3 | f(x4) |
| f(0,0,0,x4) |
Для функции 5-ти переменных:
| x1 | x2 | x3 | x4 | y(x5) |
| f(0,0,0,0,x5) f(0,0,0,1,x5) |
II. Дешифратор – КС преобразующая код, подаваемый на входы, в сигнал на одном из выходов.
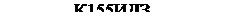 n – входов, 2n – выходов
n – входов, 2n – выходов
функциональное обозначение
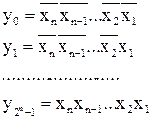
 Следовательно:
Следовательно:

Прямоугольные дешифраторы:
1 ступень – 2 линейных дешифратора
2 ступень – матричная схема
Синтез матричного дешифратора при n=4, n4=16 выходов. 
Пример 3-х ступенчатого матричного дешифратора при n=8: 
плюс – меньше аппаратуры
минус – быстродействие
 Пирамидальные дешифраторы:
Пирамидальные дешифраторы:
элемент i-ой ступени нагружен
только на 2 элемента i+1-ой ступени
Промежуточное значение между
линейным и матричным.
2.1.3. Сумматоры.
- КС для выполнения арифметических и логических операций над числами
Замечание: операция сложения в ЭВМ сложнее операции суммирования, т. к. учитывает: знаки чисел, выравниваются порядки, проводится нормализация и др.
одноразрядные или многоразрядные.
 суммирование: последовательное, параллельное, параллельно последовательное (по группам).
суммирование: последовательное, параллельное, параллельно последовательное (по группам).
I. Сложение многоразрядных чисел.
Последовательный сумматор:
слова А и В поступают с младших разрядов
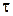 - элемент задержки на 1 такт
- элемент задержки на 1 такт
Параллельный сумматор:
Параллельно последовательный сумматор:

Пример:
в 155 серии
полный 2-х разрядный параллельный сумматор
 | |||
 | |||
 (реализация многоразрядного сумматора на ИМ1)
(реализация многоразрядного сумматора на ИМ1)

2.1.4. Триггеры.
Это КА с двумя устойчивыми состояниями. Хранит 1 бит
- регенеративная схема (собственно триггер)
- схема управления
Триггер RS-типа
| R | S | Q(t+1) |
| Q(t) неопр. |
CRS-триггер
(синхронизируемый RS-триггер).
S и R – информационные входы, С – вход синхронизации (clock – времязадающий)
| С | R | S | Q(t+1) |
| Q(t) запрещ. | |||
| Q(t) |
 |  |
D-триггер (“delay” – задержка)
Исключается возможность одновременной подачи 2-х единиц на S и R входы.
Нет запрещённых состояний.
| С | D | Q(t+1) |
| Q(t) |
Двухтактный RS-триггер.
триггер состоит из двух RS-триггеров и инвертора.
 |  |
Т-триггер (счётный)
 |  | ||||
 | |||||
JK-триггер
Тоже на базе двухтактного (универсален)
| С | J | K | Q(t+1) |
Q(t)
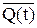
| |||
| Q(t) |

2.1.5. Регистры и счётчики.
I. Регистры.
КА предназначенный для записи, хранения и считывания слов.
Кроме того можно:
- сдвиг слова влево или вправо на требуемое число разрядов;
Дата добавления: 2016-04-06; просмотров: 757;
