Теоретические основы вычислительной техники 1 страница
1.1. Представление информации в ЭВМ
1.1.1. Системы счислении
Система счисления (СС) – это способ представления любого числа с помощью принятого набора символов (цифр, букв, …).
Представление чисел в различных системах счисления (СС)
В различных странах и в различное время исторически сложились и использовались следующие СС: римская; 5 (Африка); 12 (1фут=12дюймов, 12 месяцев…); 20 (ацтеки, майя); 60 (Вавилон – время, углы, …); 2 (Австралия, Полинезия); 10 (Индия ® арабы ® Европа).
Выбор системы счисления основывается в каждом конкретном случае на ряде критериев. Наиболее распространёнными из них являются:
- эффективность вычислений (обеспечивает простые алгоритмы);
- наглядность (определяется физическими свойствами субъекта);
- реализуемость (в данном случае – техническая).
Системы счисления классифицируются следующим образом:
Системы счисления
 |  |
непозиционные позиционные
 |  |
смешанные однородные
Различные СС связаны между собой, например: римская и десятичная.
| Римская СС | 10-я СС |
| I V X L C D M |
Пример. Представить число MDCCCXII в десятичной СС
1000(M) + 500(D) + 100(C) + 100(C) + 100(C) + 10(X) + 1(I) + 1(I) = 1812
Пример. Представить число 1988 в римской СС
1988 = 1000+900+80+8 = 1000+(1000-100)+50+10+10+10+5+1+1+1= =MCMLXXXVIII
MDCCCXII – 1812 XXX – 30
XL – 40
LXXX – 80
XC – 90
CCC – 300
CD – 400
DC – 600
CM – 900
Позиционная СС (ПСС) определяется конфигурацией и местом (позицией) каждого элемента, а характеризуется: основанием (числом символов n) и алфавитом.
Представление позиционной СС полиномом

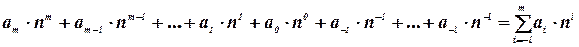
где n – основание СС, ai – любой символ из алфавита СС
Примеры ПСС.
| СС | основание | алфавит |
| десятичная двоичная восьмеричная шестнадцатеричная | 0 1 2 3 4 5 6 7 8 9 0 1 0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8 9 A B C D E F |
Однородной СС является система, у которой в каждом разряде одинаковое число цифр. С теоретической точки зрения оптимальной ЭВМ является та, у которой основание системы счисления – е (ближайшее число 3), а с практической используется основание кратное 2 (это определено существующей технологической базой: триггеры – 2 состояния).
Задание 1. Представить число 1539 в римской С. С.
Задание 2. Представить число MMDCXLVII в 10-ной С. С.
Задание 3. Представить число 15.394(10) полиномом.
Задание 4. Представить число 11010100,001 полиномом.
1.1.2. Методы перевода чисел из одной позиционной системы счисления в другую.
A(n)=>A(k), где А – число, n и k – основания двух С. С.
Алгоритм перевода при n<k:
- представить А(n) полиномом основания n,
- все коэффициенты, основание n-ичной С. С. и все степени основания полинома записать в k-ичной С. С.,
- выполнив все предусмотренные действия получить А(k).
Пример. Перевести число 1011,01 из двоичной С. С. в десятичную С. С.
Здесь n = 2, k = 10, т. е. n<k.
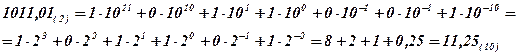
Задание 5. Перевести число 10001,011(2) в десятичную С. С.
Задание 6. Перевести число 0,10011(2) в десятичную С. С.
Алгоритм перевода при n>k. Преобразуются отдельно и по-разному целая Ац(n) и дробная Ад(n) части числа А(n).
А(n) = Aц(n)+Aд(n).
Преобразование Ац(n)=>Aц(k) осуществляется последовательным делением Ац(n) на k, выделением остатков от деления и составлением из них числа Ац(k).
Пример. Перевести число 37,75 из десятичной С. С. в двоичную С. С. Здесь n=10, k=2, т. е. n>k.
А(10)=Ац(10)+Ад(10)=37(10)+0,75(10). Нужно Ац(10)=>Ац(2) и Ад(10)=>Aд(2).
| x0, | |
| а-1=1, | |
| а-2=1, | |
| а-3=0 |
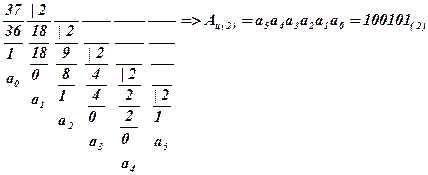
=> Aд(2)=0,а-1а-2а-3…=0,11(2)
В итоге: 37,75(10)=100101,11(2)
Проверка: 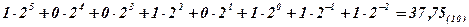
Задание 7. Перевести число 29,8125(10) в двоичную С. С.
Задание 8. Перевести число 100,3(10) в двоичную С. С.
Задание 9. Перевести число 364(7) в пятеричную С. С. через десятичную С. С.
Перевод чисел в С. С. с основанием кратным двум.
Пусть n=2l, а k=2. Тогда каждая цифра n-ичной С. С. представляется l – разрядным двоичным числом.
Пример. Перевести число 472,54(8) в двоичную и шестнадцатеричную С. С.
Сначала выполним перевод в двоичную С. С.
Так как 16=24, то l2 и, следовательно,
472,54(8)= 100111010 , 1011 = 1 3 А , В(16).
Задание 10. Перевести число 3103,12(4) в двоичную С. С.
Задание 11. Перевести число 1011010101,11(2) в восьмеричную С. С. и шестнадцатеричную С. С.
Задание 12. Перевести число F0A(16) в четвертичную С. С.
Задание 13. Перевести число 27,59375(10) в шестнадцатеричную С. С.
1.1.3. Формы представления чисел.

Представление чисел в форме с фиксированной запятой (ФЗ)
Формат представления чисел с запятой, фиксированной перед старшим разрядом:
| , | знак | 2-1 | 2-2 | 2-3 | 2-(n-2) | 2-(n-1) | <= веса разрядов | |
| -2 | -1 | <= номера разрядов |
n – разрядная сетка ЭВМ
В этом формате диапазон представляемых чисел 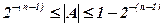
Формат представления чисел с запятой, фиксированной после младшего разряда:
| знак | 2n-2 | 2n-3 | 2n-4 | 21 | 20 | |
| n-1 | n-2 | n-3 | n-4 |
В этом формате диапазон представляемых чисел 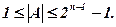
Представление знаков: “+” <==> 0; “-“ <==> 1.
Пример. Представить число -0,0225(10) в форме с ФЗ в 16-разрядной сетке ЭВМ.
-0,0225(10)=-0,0000010111(2).
| , |
Формат представления чисел в форме с естественной запятой.
(с произвольным расположением запятой в пределах n-разрядной сетки ЭВМ)
| знак | 2l-1 | 2l-2 | 21 | 20 | , | 2-1 | 2-(m-1) | 2-m | ||
| целая часть числа (l разрядов) | дробная часть числа (m разрядов) | |||||||||
| n – разрядная сетка ЭВМ (n=l+m+1) |
Задание 14. Представить число 1141(10) в форме с ФЗ в 16-разрядной сетке.
Задание 15. Представить число -0,4(10) в форме с ФЗ в 8-разрядной сетке.
Задание 16. Представить число -88,8125(10) в форме с естественной запятой в 16-разрядной сетке.
Представление чисел в форме с плавающей запятой (ПЗ).
Число представляется в виде: 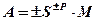 , где А – исходное число, М – мантисса (/М/<1), SP – характеристика числа А, S – основание С. С., Р – порядок.
, где А – исходное число, М – мантисса (/М/<1), SP – характеристика числа А, S – основание С. С., Р – порядок.
| знак порядка | знак числа | ||||||
| разряды Р | разряды М | ||||||
| l разрядов | m разрядов |
При таком представлении чисел необходимо проведение их нормализации. Число А называется нормализированным, если мантисса удовлетворяет условию 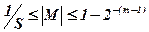 , т. е. если старший разряд мантиссы отличен от нуля.
, т. е. если старший разряд мантиссы отличен от нуля.
Пример. Представить число -27,375(10) в форме с ПЗ в 16-разрядной сетке ЭВМ.
-27,375(10)=-11011,011(2). Проведя нормализацию получим 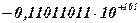 . Пусть под порядок отведено 4 разряда. Тогда содержимое разрядной сетки будет:
. Пусть под порядок отведено 4 разряда. Тогда содержимое разрядной сетки будет:
Задание 17. Представить число 59,625(10) в форме с ПЗ в 16-разрядной сетке.
Задание 18. Представить число -0,0625(10) в форме с ПЗ в 8-разрядной сетке.
Задание 19. Представить число -6,025(10) в форме с ПЗ в 32-разрядной сетке.
Задание 20. Представить число 0,1Е(16) в форме с ПЗ в 16-разрядной сетке.
Представление чисел в форме с ПЗ и смещённым порядком.
Смещённый порядок 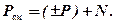 Здесь
Здесь 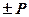 - истинный порядок, а N=2k, где число k – число двоичных разрядов отведённое для представления
- истинный порядок, а N=2k, где число k – число двоичных разрядов отведённое для представления 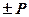 (или Рсм). Всегда Рсм>0.
(или Рсм). Всегда Рсм>0.
Короткий (32 разряда) формат представления чисел с ПЗ и смещённым порядком в ЕС ЭВМ
| знак числа | Рсм | мантисса | |||||
0 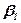 1 3 1 3
| 4 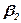 7 7
| 8 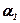 11 11
| 12 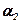 15 15
| 16 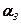 19 19
| 20 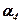 23 23
| 24 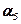 27 27
| 28 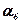 31 31
|
Здесь 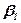 ,
, 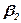 ,
, 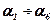 - шестнадцатеричные разряды. Следовательно содержимое разрядной сетки может быть представлено числом
- шестнадцатеричные разряды. Следовательно содержимое разрядной сетки может быть представлено числом 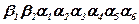 . При таком представлении нормализация проводится для шестнадцатеричного числа. При определении смещённого порядка число N в шестнадцатеричной С. С. будет равно 40(16).
. При таком представлении нормализация проводится для шестнадцатеричного числа. При определении смещённого порядка число N в шестнадцатеричной С. С. будет равно 40(16).
В ЕС ЭВМ существуют также длинный (64 двоичных разряда) и расширенный (128 двоичных разряда) форматы. В них расширяется только поле отводящееся под мантиссу.
Пример. Представить число -0,01(10) в форме с ПЗ и смещённым порядком в коротком формате ЕС ЭВМ.
Переведём число в шестнадцатеричную С. С. 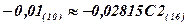 . Проведя нормализацию этого числа получим мантиссу (-0,2815С3)(16), а порядок (-1)(16). Определим смещённый порядок.
. Проведя нормализацию этого числа получим мантиссу (-0,2815С3)(16), а порядок (-1)(16). Определим смещённый порядок.
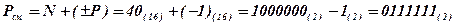 .
.
Расположим число в 32-х разрядной сетке
| знак числа | Р | М | ||||||
| 0 1 1 | 1 1 1 1 | 0 0 1 0 | 1 0 0 0 | 1 1 1 1 | 0 1 0 1 | 1 1 0 0 | 0 0 1 1 | |
| B | F | F | C |
Следовательно в памяти ЕС ЭВМ число -0,01(10) будет представлено шестнадцатеричным словом BF28F5C3.
Задание 21. Представить число -43,375(10) в форме с ПЗ и смещённым порядком в коротком формате ЕС ЭВМ. Содержимое разрядной сетки представить 16-ричным словом.
Задание 22. Представить число 17,1(10) в форме с ПЗ и смещённым порядком в длинном формате ЕС ЭВМ.
Задание 23. Представить число -0,0625(10) в форме с ПЗ и смещённым порядком в коротком формате ЕС ЭВМ. Содержимое разрядной сетки представить 16-ричным словом.
Задание 24. Содержимое 32-х разрядной сетки ЕС ЭВМ представлено словом С3180000(16). Определить какое десятичное число записано в разрядной сетке.
1.1.4. Представление алфавитно-цифровой информации.
Используются различные системы соответствия символов (цифр, букв, математических и служебных знаков) их двоичному представлению. Это ДКОИ – двоичный код для обработки информации (8 разрядное представление символа), КОИ-8 – код обмена информацией (8 разрядов), КОИ-7 – код обмена информацией (7 разрядов).
| байт | байт | байт | |
| символ | символ | символ | |
| алфавитно-цифровая информация Соответствующие таблицы кодирования символов даны в [1]. |
Пример. Представить запись «СМ-4» в ДКОИ.
| байт | байт | байт | байт |
| С | М | - |
Система представления данных состоящих только из десятичных цифр использует двоично-десятичное кодирование. Соответствие десятичных цифр их 2-10-м кодам дано в таблице 1. Не используемые в таблице 1 комбинации (1010 – 1111) применяются для представления значков чисел и зоны в соответствии с табл. 2.
Таблица 1
| десятичная цифра | 2-10 код |
| … | … |
Таблица 2
| ДКОИ | КОИ-8 | |
| + - зона |
Существуют два специальных формата для многоразрядных десятичных чисел:
зонный формат
| зона | цифра | зона | цифра | знак | цифра | |
| байт | байт | байт |
упакованный формат
| цифра | цифра | цифра | знак | |
| байт | байт |
В упакованном формате число байтов должно быть целым.
Пример. Представить десятичное число -5901 в зонном и упакованном форматах ДКОИ.
| зона | зона | зона | знак | число в зонном формате |
| (*) | знак | число в упакованном формате (*) – дополнение до целого числа байтов |
Задание 25. Представить запись «A/B-I» в ДКОИ и КОИ-8 используя таблицы в [1].
Задание 26. Представить последовательность десятичных чисел -17+0-10 в зонном формате ДКОИ.
Задание 27. Представить последовательность десятичных чисел +10-187-4 в упакованном формате КОИ-8.
Арифметические основы вычислительной техники.
Так как двоичная С. С. и десятичная С. С. принадлежат к одному классу позиционных аддитивных С. С. с естественным порядком весов, то правила выполнения арифметических операций над числами в этих С. С. одинаковы.
Пример. Выполнить четыре арифметических операции над числами
А=1001(2) и В=11(2).
| +1001 |
| –1001 |
| х1001 |
| -1001 | |
| -011 | |
1.2. Арифметические основы вычислительной техники.
1.2.1. Прямой, обратный и дополнительный коды чисел.
Коды целых и дробных чисел, представленных в форме с ФЗ, формируются одинаково. Вопрос о том, какое число закодировано – целое или дробное, решается по формату с которым работает ЭВМ.
Прямой код представляет собой запись самого числа с соответствующим знаком. Знак «+» кодируется 0, а знак «–» кодируется 1 и записывается крайним слева (для наглядности будем выделять знаковый разряд рамкой).
Обратный код положительного числа совпадает с его прямым кодом. Обратный код отрицательного числа формируется из прямого путём инвертирования цифр во всех разрядах за исключением знакового.
Дополнительный код положительного числа совпадает с его прямым кодом. Дополнительный код отрицательного числа формируется добавлением единицы к младшему разряду обратного кода этого числа.
Задание 28. Представить число -0,111(2) в прямом, обратном и дополнительных кодах.
Задание 29. Представить число -10000(2) в прямом, обратном и дополнительных кодак.
1.2.2. Сложение и вычитание двоичных чисел.
Сложение и вычитание чисел представленных в форме с ФЗ.
Сложение и вычитание чисел А и В в форме с ФЗ сводится в ЭВМ к суммированию обратных или дополнительных кодов этих чисел с учётом знаков.
При суммировании дополнительных кодов чисел А и В сумма S получается в дополнительном коде: Адоп+Вдоп=Sдоп.
При суммировании обратных кодов чисел А и В сумма S получается в обратном коде: Аобр+Вобр=Sобр
всегда, за исключением случая, когда В<0. В этом случае, если есть перенос из знакового разряда, нужна коррекция результата суммирования S’ путём добавления 1 к его младшему разряду, т. е. при B<0: Аобр+Вобр=S’+1=Sобр.
Для этого используется перенос из знакового разряда.
Пример. Выполнить суммирование чисел 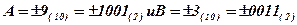 в обратном и дополнительном кодах при всех возможных комбинациях знаков.
в обратном и дополнительном кодах при всех возможных комбинациях знаков.
Представим результаты вычислений таблицей и в каждой графе проведём проверку результата переводом его в прямой код Sпр.
А=9 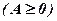 В=3
В=3 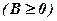
| А=-9 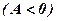 В=3
В=3 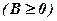
| А=9 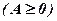 B=-3 (B<3)
B=-3 (B<3)
| A=-9 (A<0) B=-3 (B<0) | |||||||||||||
| +Аобр= | +Аобр= | +Аобр= | +Аобр= | |||||||||||||
| Вобр= | Вобр= | Вобр= | Вобр= | |||||||||||||
| Sобр= | Sобр= | S’= | S’= | |||||||||||||
| +1 | +1 | |||||||||||||||
| Sобр= | Sобр= | |||||||||||||||
| Sпр=Sобр= +12(10) | Sпр= | 0110=-6(10) | Sпр=Sобр=+6(10) | Sпр= | 1100=-12 | |||||||||||
| +Адоп= | +Адоп= | +Адоп= | +Адоп= | |||||||||||||
| Вдоп= | Вдоп= | Вдоп= | Вдоп= | |||||||||||||
| Sдоп= | Sдоп= | Sдоп= | Sдоп= | |||||||||||||
| Sпр=Sдоп= +12(10) | Sпр= | 0110=-6(10) | Sпр=Sдоп=+6(10) | Sпр= | 1100=-12 | |||||||||||
Задание 30. Выполнить суммирование чисел -7 и 5 в обратном и дополнительном кодах.
Задание 31. Выполнить суммирование чисел 14 и -10 в обратном и дополнительных кодах.
Задание 32. Выполнить суммирование чисел -8 и -6 в обратном и дополнительных кодах.
При выполнении операции суммирования кодов чисел, представленных в форме с ФЗ, возможно переполнение разрядной сетки ЭВМ. Существуют следующие признаки переполнения:
- одинаковые знаковые разряды слагаемых отличаются от знака результата;
- в процессе суммирования значение переносов из старшего и из знакового разрядов не совпадают.
Пример. Определить факт переполнения разрядной сетки ЭВМ при суммировании чисел 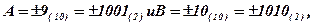 представленных в обратном и дополнительном кодах при всех возможных комбинациях знаков.
представленных в обратном и дополнительном кодах при всех возможных комбинациях знаков.
Переполнение возможно лишь при равенстве знаков суммируемых чисел поэтому рассмотрим лишь пары чисел А>0, B>0 и A<0, B<0.
| A=+9 (A>0) B=+10 (B>0) | A=-9 (A<0) B=-10 (B<0) | A=-9 (A<0) B=-10 (B<0) | |||||||
| +Аобр=Адоп= Вобр=Вдоп= | +Аобр= Вобр= | +Адоп= Вдоп= | |||||||
| S= | S’= | Sдоп= | |||||||
| +1 | |||||||||
| Sобр= | |||||||||
В обоих случаях произошло переполнение выявляемое по любому из приведённых выше признаков. Например, знак результата в каждом случае отличается от знаковых разрядов слагаемых, а значения переносов не совпадают.
Задание 33. Определить, возникнет ли переполнение разрядной сетки при суммировании чисел 7(10) и 11(10).
Задание 34. По какому признаку можно определить факт переполнения разрядной сетки при суммировании чисел -13(10) и -8(10).
Сложение и вычитание чисел, представленных в форме с ПЗ.
Выполнение операций сложения и вычитания двоичных чисел 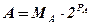 и
и 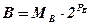 в форме с ПЗ аналогично соответствующим операциям над числами в форме с ФЗ, если выполняется условие РА=РВ. Если
в форме с ПЗ аналогично соответствующим операциям над числами в форме с ФЗ, если выполняется условие РА=РВ. Если 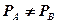 , то необходимо:
, то необходимо:
- провести предварительное выравнивание порядков, что приводит к денормализации одной из мантисс;
- провести нормализацию результата операции, если мантисса результата 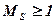 или МS<0,5. При
или МS<0,5. При 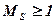 нужна нормализация вправо, а при МS<0,5 – нормализация влево.
нужна нормализация вправо, а при МS<0,5 – нормализация влево.
Дата добавления: 2016-04-06; просмотров: 938;
