Некогерентного приема в двоичной системе связи
Для определения средней вероятности ошибки оптимального некогерентного приема в двоичной системе при равных вероятностях передаваемых сообщениях P(b0) = P(b1) достаточно вычислить условную вероятность ошибки любого типа, как это было установлено в разделе 6.4,
.
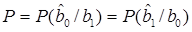Вычислим 
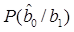, ориентируясь на схему некогерентного демодулятора на СФ (рис. 6.37). Ошибка вида 
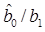(при передаче сообщения b1 принимается решение в пользу 
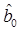) возникает, если для отсчетов огибающих на выходах ветвей демодулятора выполняется неравенство 
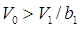. Для определения его вероятности
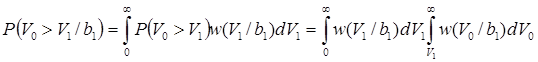
надо знать плотности вероятност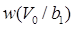и 
и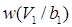 
, вычислением которых и займемся. Вспомним, что
,
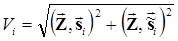где i – номер ветви (индекс сигнала, на который настроен СФ)
,
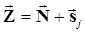j – индекс передаваемого сообщения.
.
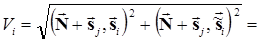
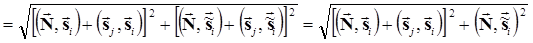Запишем отсчеты огибающих V0 и V1 на выходах соответствующих ветвей демодулятора при передаче сигнала s1(t) (j = 1)
i = 0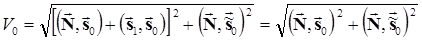 
i = 1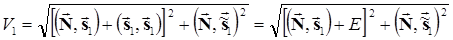 
.
Входящие в эти выражения скалярные произведения
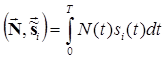
представляют собой нормально распределенные случайные величины с нулевым математическим ожиданием, следовательно, огибающие Vi будут иметь распределение Рэлея на выходе СФ0 (i = 0)
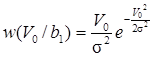
и обобщенное распределение Рэлея на выходе СФ1 (i = 1)
.
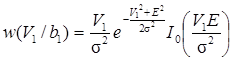Вернемся к вычислению средней вероятности ошибки при оптимальном некогерентном приеме
.
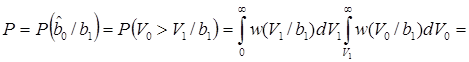
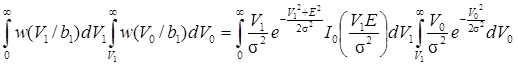Произведя замену переменных
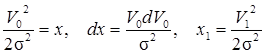
получим
.
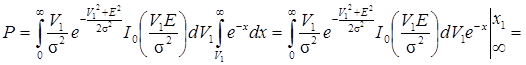
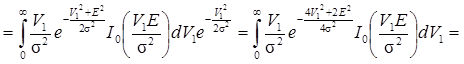
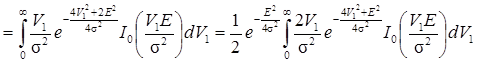Обозначим 2V1=V, 2σ2 = g2, тогда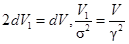 
и
.
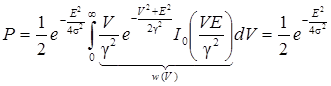Здесь учтено то, что подынтегральное выражение можно трактовать как плотность вероятности обобщенного распределения Рэлея (5.13).
Вычислим σ2 – мощность шума на выходе СФ
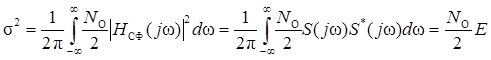
и окончательно получим
,
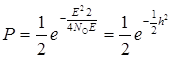где, как и ранее,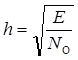 
.
Полученный результат относится к любым двоичным системам, использующим ортогональные в усиленном смысле сигналы.
Нетрудно сообразить, что для некогерентного приема в двоичных системах с пассивной паузой (АМ)
.
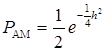Некогерентный прием сигналов с ФМ исключается, т.к. огибающие противоположных сигналов неразличимы, однако возможна реализация оптимального некогерентного демодулятора для системы с ОФМ (рис. 6.38), сигналы которой ортогональны в усиленном смысле на двойном интервале 2Т и, следовательно, имеют на этом интервале удвоенную энергию. По этой причине
.
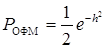На рис. 6.39. приведены кривые помехоустойчивости оптимального некогерентного приема сигналов с АМ, ЧМ и ОФМ.
На практике используют также квазиоптимальный прием ЧМ сигналов, применяя в схеме (рис. 6.37) вместо СФ (согласованных с сигналами по их форме) полосовые фильтры (ПФ) с прямоугольной АЧХ, согласуя их с шириной спектра сигналов. В.И.Сифоровым было установлено, что максимальное отношение с/ш на выходе ПФ с прямоугольной АЧХ достигается при ширине полосы пропускания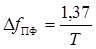 
и оно, естественно, несколько меньше, чем для СФ (энергетический проигрыш 0,86 дБ). Дополнительное снижение помехоустойчивости при использовании ПФ вызывается межсимвольной интерференцией, возникающей из-за наложения переходных процессов от предшествующих посылок на последующие (что не имеет места при согласованной фильтрации).
Контрольные вопросы
1. Сформулируйте задачу синтеза оптимального некогерентного демодулятора.
2. Напишите алгоритм оптимального приема дискретных сообщений в канале с неопределенной фазой.
3. Как упрощается алгоритм некогерентного приема при условии равенства энергий используемых сигналов?
4. Нарисуйте схему оптимального некогерентного демодулятора для системы сигналов с разными энергиями.
5. Нарисуйте схему оптимального некогерентного демодулятора для системы сигналов с равными энергиями.
6. Как вычисляется огибающая Vi.
7. Нарисуйте схему блока определения огибающей Vi.
8. Нарисуйте схему оптимального некогерентного демодулятора на согласованных фильтрах.
9. Что означает ортогональность сигналов в усиленном смысле?
10. Почему для достижения максимальной помехоустойчивости некогерентного приема требуется использование ортогональных в усиленном смысле сигналов?
11. Приведите примеры систем ортогональных в усиленном смысле сигналов.
12. При каких видах цифровой модуляции возможен некогерентный прием сигналов?
13. Изложите методологию расчета средней вероятности ошибок при оптимальном некогерентном приеме.
14. Почему возможен некогерентный прием сигналов с ОФМ, а с ФМ – нет?
15. Приведите формулы для вычисления средней вероятности ошибочного некогерентного приема АМ, ЧМ и ОФМ сигналов.
16. Что называют квазиоптимальным некогерентным приемом? В чем его достоинства и недостатки?
Дата добавления: 2016-04-02; просмотров: 642;