Потенциальная помехоустойчивость когерентного приема

Постановка задачи:

Известны:

1. Ансамбль сигналов на выходе модулятора

{s_i(t)}_m; i = 1, 2,…, m; t Î (0, T).

2. Непрерывный канал

,

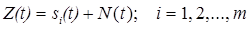где N(t) – квазибелый нормальный шум, т. е.

.

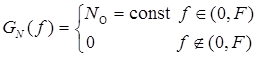3. Алгоритм работы демодулятора (оптимального когерентного по критерию максимального правдоподобия) (6.13)

.

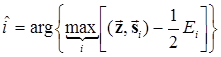ОпределитьР - среднюю вероятность ошибочного приема.

Ограничимся случаем двоичной системы (m = 2), когда

.

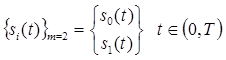Перепишем алгоритм (6.13) в развернутом виде

,

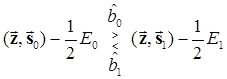или

.

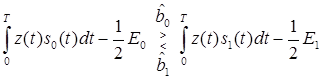Из иной записи того же алгоритма

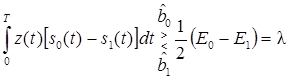
вытекает достаточность одной ветви в оптимальном демодуляторе, которая должна содержать либо коррелятор с опорным генератором разностного сигнала, либо согласованный с этим разностным сигналом фильтр (рис. 6.25). В этих демодуляторах в качестве решающих устройств используются компараторы со стробированием. Компаратор представляет собой дифференциальный усилитель с цифровым выходом и коэффициентом усиления К ® ¥. Напряжение на выходе компаратора может принимать одно из двух значений: высокое (уровень логической «1»), если напряжение на его прямом входе больше, чем на инверсном, и низкое (уровень логического «0») в противном случае. В данном случае производится сравнение выходного напряжения коррелятора или СФ с пороговым в моменты kT поступления коротких стробирующих импульсов. Символом «= =» в УГО компаратора обозначена операция сравнения, а кружком – инверсный вход.

Для решения поставленной задачи рассмотрим случайную величину Y_D(T) – отсчеты реакции СФ в конце каждого сигнала на входной СП Z(t) = s_i(t) + N(t). Очевидно, что Y_D(T) имеет нормальное распределение с двумя возможными математическими ожиданиями :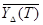

y₀ – при передаче сообщения b₀,

y₁ – при передаче сообщения b₁.

, .

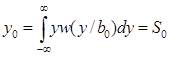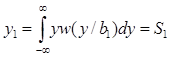Условные распределения величины Y_D(T) показаны на рис. 6.26

В двоичных системах имеют место ошибки двух типов. Определим их вероятности

, .

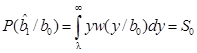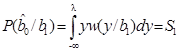Средняя вероятность ошибочного приема

.

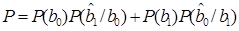При равных вероятностях передаваемых сообщений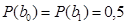

.

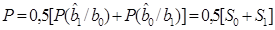Минимизация Р означает минимизацию суммы S₀ + S₁, что достигается при выборе оптимального порога λ_опт, определяемого из условия 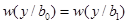(рис. 6.26)

.

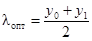При таком выборе порога

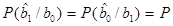
и, следовательно, для вычисления средней вероятности ошибочного приема Р достаточно определить любую условную вероятность ошибок, например,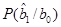

.

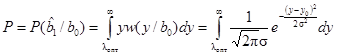Произведя замену переменных

,

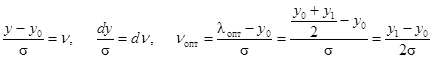получим

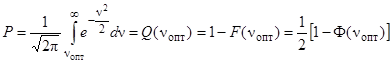, (6.18)

где Q(ν_опт) – дополнительная функция ошибок,

F(ν_опт) – функция ошибок,

Ф(ν_опт) – функция Крампа.

Все эти функции табулированы, их можно найти в математических справочниках.

Полученный результат свидетельствует, что для любой двоичной системы при когерентном приеме вероятность ошибок определяется исключительно величиной ν_опт, на которой сосредоточим свое внимание. Из рассмотренного вытекает

,

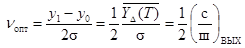где 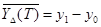– математическое ожидание отклика фильтра, согла-

сованного с разностным сигналом s_Э(t) = s₁(t) – s₀(t),

на «свой» сигнал в момент t = T,

σ – квадратный корень из дисперсии этого отклика.

Используя ранее вычисленное значение отношения с/ш на выходе согласованного фильтра (6.17), получаем

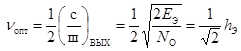, (6.18)

где Е_Э – энергия разностного (эквивалентного) сигнала s_э(t),

N_O – спектральная плотность мощности шума,

.

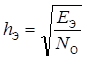Учитывая геометрический смысл энергии сигнала 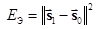, выражение (6.18) можно переписать в виде

.

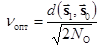Выводы

1. Помехоустойчивость когерентного приема в двоичных системах определяется исключительно соотношением энергии Е_Э разностного сигнала (расстоянием между сигналами) и спектральной плотности мощности N_O нормального белого шума

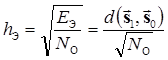. (6.19)

2. Средняя вероятность ошибочного приема для этого случая вычисляется с помощью дополнительной функции ошибок по формуле

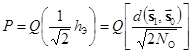(6.20)