Спектральный анализ случайных процессов

Спектральный анализ детерминированных сигналов x(t) предпо-лагает использование прямого преобразования Фурье

.

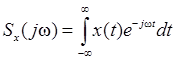Распространение этого подхода на случайные процессы наталкивается на ряд серьезных проблем:

1. существует только для функций x(t), удовлетворяющих условию абсолютной интегрируемости

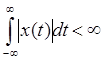
или хотя бы интегрируемости в квадрате

,

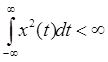т.е. для сигналов с ограниченной энергией. Однако реализации стационарных случайных процессов с вероятностью 1 имеют бесконечную энергию, так как по определению существуют на бесконечной оси времени и, следовательно, этим требованиям не отвечают. Эту трудность можно обойти, если рассматривать отношение спектральной функции к длительности сигнала Т. Тогда достаточным будет требование ограниченной мощности сигнала x(t)

.

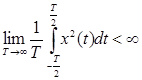2. Спектральная функция характеризует отдельные реализации x(t) случайного процесса X(t), а не сам процесс целиком. Попытка перейти, как обычно, к усреднению по ансамблю оказывается несостоятельной. Действительно, если определить математическое ожидание случайной спектральной функции

,

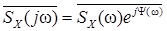где - амплитудный, а - фазовый спектры случайного процесса X(t), то для независимых и при равномерном распределении в интервале 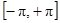получим нулевой результат усреднения для ненулевых процессов.

Выход из этой ситуации состоит в отбрасывании фазового и усреднении только амплитудного спектра 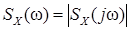или .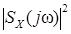

Для реализаций случайных процессов X(t) с ограниченной энергией Е_х (нестационарных) по теореме Парсеваля имеем

,

где - спектральная плотность энергии реализации x(t).

Усредняя по ансамблю реализаций, получим 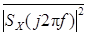– спектральную плотность энергии случайного процесса X(t) с размерностью

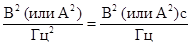, что соответствует размерности 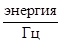, если иметь в виду действие X(t) на сопротивлении 1 Ом.

Для стационарных случайных процессов на интервале Т рассмотрим функцию , имеющую размерность 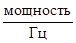. Переходя к пределу при , получим спектральную плотность мощности

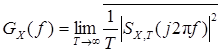, (4.1)

называемую также энергетическим спектром процесса X(t).

Энергетический спектр стационарного случайного процесса и его корреляционная функция связаны между собой интегральными преобразованиями Фурье, что было строго доказано А.Я. Хинчиным и Н. Винером (теорема Винера-Хинчина)

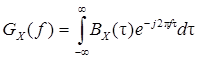, (4.2)

. (4.3)

Рассмотрим нестрогое доказательство этой теоремы с прозрачным смыслом. Исходя из вышеприведенного определения энергетического спектра, имеем

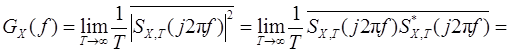
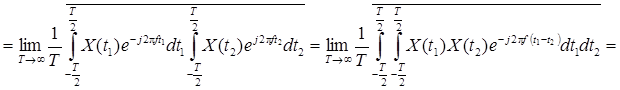
(после замены переменных )

(после замены усреднения по ансамблю усреднением по времени)

,

что и требовалось доказать.