Понятие случайного процесса. Математические модели случайных процессов

Математические модели случайных процессов

Сигналы в системах передачи информации и действующие в них помехи по своей природе являются случайными процессами. Для их описания необходимо применять математический аппарат теории вероятностей и случайных процессов. Настоящую главу следует рассматривать как развитие раздела 2. Математические модели сигналов (Теория электрической связи. Конспект лекций. Часть 1) применительно к случайным процессам.

Понятие случайного процесса

x_k(t) x₁(t) x₂(t) t_i t Рис. 4.1. Реализации процесса X(t)

Случайный процесс(СП) X(t) является функцией времени, значения которой в любой фиксированный момент времени t_i представляют собой случайную величину X(t_i). Здесь и в дальнейшем случайные величины и функции будем обозначать заглавными буквами, а детерминированные (неслучайные) – строчными, как это широко принято. На рис. 4.1 изображены возможные реализации x₁(t) и x₂(t) случайного процесса X(t), являющиеся детерминированными функциями времени. Сам процесс можно трактовать как множество (в том числе и несчетное) подобных реализаций { x_k(t) } с соответствующей вероятностной мерой.

Для полного описания сечений X(t_i) СП необходимо указать законы распределения значений СП в этих сечениях. Они могут быть заданы в интегральной (функция распределения) или дифференциальной (плотность вероятности) формах. В таблице 4.1., в порядке напоминания, приведены основные сведения об этих законах и их свойствах.

Таблица 4.1

Название и обозначение	Функция распределения F(x)	Плотность вероятности w(x)
Определение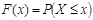
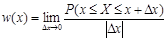
Физическая размерность	безразмерная	размерность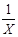
Взаимосвязь
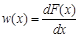
Особенности функции	F(x₂)³ F(x₁) при x₂> x₁ (неубывающая)	w(x)³0 (неотрицательная)
Расчет вероятности
Свойство нормировки

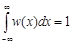
Примеры распределений случайных величин:

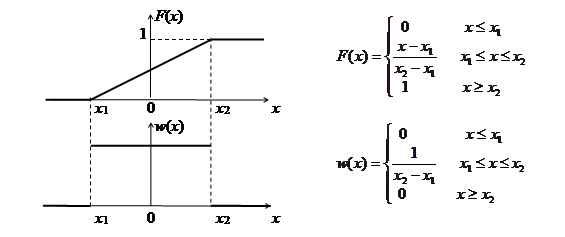Равномерное

Нормальное (гауссовское)

Распределение дискретной случайной величины

F(x) x x₁ x₂ x₃ x₄ w(x) x x₁ x₂ x₃ x₄

Информация о сечениях СП не является достаточной для описания самого СП, так как не содержит сведений о зависимостях сечений между собой. Исчерпывающее описание СП осуществляется с помощью n-мерной функции распределения

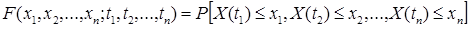
или n-мерной плотности вероятности

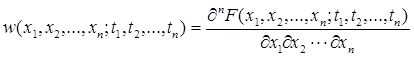где x_1,x_2…, x_n – аргументы, t₁, t₂…, t_n – параметры этих функций, а n – любое целое число.

Если n-мерная функция распределения (плотность вероятности) СП не меняется при сдвиге всех моментов t_k (k = 1, 2, …, n) на один и тот же интервал Dt, то такой процесс называют стационарным в узком смысле.

<12 3 4 5 6 7 >

Дата добавления: 2016-04-02; просмотров: 943;