Сокращенное описание случайных процессов
Полное описание СП не всегда возможно, да и не всегда требуется. Во многих случаях достаточно знать основные его характеристики. В качестве таковых широко используют:
1. Математическое ожидание СП – начальный момент первого порядка
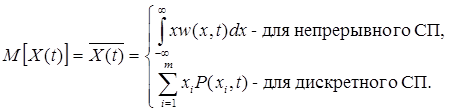
2. ДисперсияСП – центральный момент второго порядка
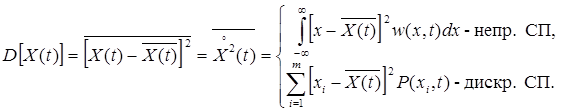
Здесь использовано понятие центрированного СП 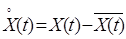 .
.
3. В общем случае можно использовать моменты k-го порядка:
Начальные
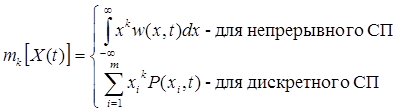 ,
,
Центральные
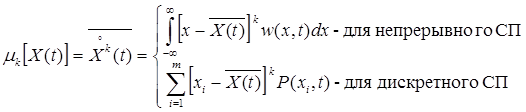 .
.
Нетрудно видеть, что моменты полностью определяются одномерным распределением и в общем случае произвольного СП являются детерминированными функциями времени. Для стационарных в узком смысле СП моменты от времени не зависят.
1. Корреляционная (автокорреляционная) функция – центральный смешанный момент второго порядка
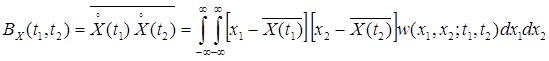 .
.
Случайные процессы называют стационарными в широком смысле, если выполняются следующие условия:
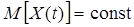 ,
,
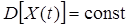 ,
,
 , где τ = t2 – t1
, где τ = t2 – t1
Очевидно, что стационарность СП в узком смысле влечет его стационарность в широком смысле, но не наоборот.
Некоторые свойства корреляционной функции СП:
1. 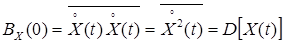
2. 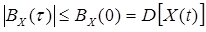
Доказательство:
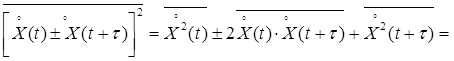
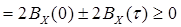 ,
,
откуда следует вышеуказанное неравенство
3. Корреляционная функция характеризует статистическую связь сечений СП (внутри процесса). Если связи между сечениями 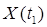 и
и 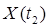 нет (сечения статистически независимы), то
нет (сечения статистически независимы), то  .
.
Доказательство:

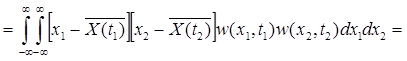
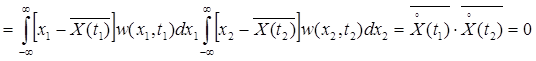 .
.
Отсутствие связи влечет отсутствие корреляции, но не наоборот. Обратное утверждение справедливо лишь в случае нормального (гауссовского) процесса.
Нормальным называют СП, у которого одномерная плотность вероятности имеет вид
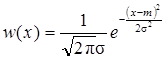 ,
,
где 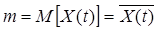 ,
, 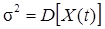 ,
,
а любая n-мерная плотность вероятности описывается выражением
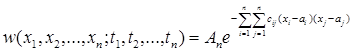 ,
,
где An, cij, ai, aj – константы, определяемые выбором сечений t1,t2,,,tn.
4. Корреляционная функция стационарного случайного процесса является четной 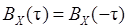 .
.
Доказательство:
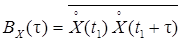 .
.
Подставляя 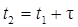 , получим
, получим
 .
.
5. Чтобы абстрагироваться от дисперсии и учитывать только связи внутри СП удобно пользоваться нормированной функцией корреляции (коэффициентом корреляции)
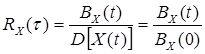 .
.
Очевидно, что 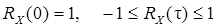 .
.
6. Интервал корреляции – грубую числовую оценку связи внутри СП – чаще всего определяют методом равновеликого прямоугольника
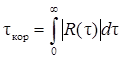 .
.
7. Взаимная корреляционная функция двух процессов X(t) и Y(t)
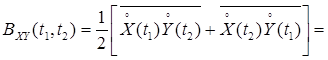
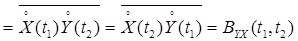 .
.
8. Корреляционная функция суммы независимых случайных процессов 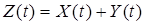 есть сумма корреляционных функций каждого из слагаемых СП в отдельности
есть сумма корреляционных функций каждого из слагаемых СП в отдельности 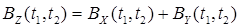
Доказательство:
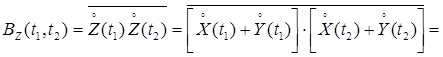
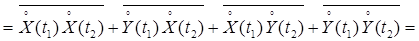
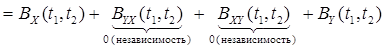 .
.
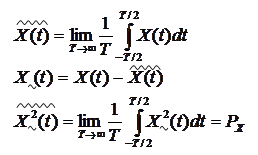 Вместо усреднения по множеству реализаций случайного процесса можно ввести его усреднение по времени, определяя:
Вместо усреднения по множеству реализаций случайного процесса можно ввести его усреднение по времени, определяя:
- постоянную составляющуюСП,
- переменную составляющуюСП,
- мощность переменной состав-
ляющейСП.
Нетрудно видеть, что эти характеристики являются случайными величинами, не зависящими от времени.
 Случайные стационарные процессы называют эргодическими, если их усреднение по множеству и по времени приводит к одинаковым результатам:
Случайные стационарные процессы называют эргодическими, если их усреднение по множеству и по времени приводит к одинаковым результатам:
|
 Эргодическое свойство СП заключается, грубо говоря, в том, что все его реализации «похожи» друг на друга. Отсюда следует возможность получения вышеуказанных характеристик эргодического СП усреднением по времени единственной его реализации x(t), что существенно облегчает построение аппаратуры для их измерений. В частности, функцию корреляции эргодического СП можно вычислить по одной реализации с помощью следующего выражения:
Эргодическое свойство СП заключается, грубо говоря, в том, что все его реализации «похожи» друг на друга. Отсюда следует возможность получения вышеуказанных характеристик эргодического СП усреднением по времени единственной его реализации x(t), что существенно облегчает построение аппаратуры для их измерений. В частности, функцию корреляции эргодического СП можно вычислить по одной реализации с помощью следующего выражения:
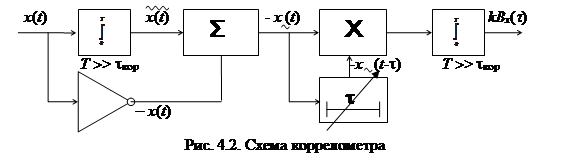 из которого вытекает схема коррелометра, приведенная на рис. 4.2.
из которого вытекает схема коррелометра, приведенная на рис. 4.2.
Дата добавления: 2016-04-02; просмотров: 963;

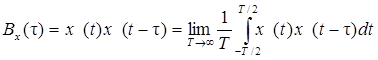 ,
,