Понятие о статистических рядах распределения, их виды, составные элементы, графическое изображение

Ряды распределения – это упорядоченное распределение единиц совокупности на группы по изучаемому варьирующему признаку.

В зависимости от признака, положенного в основу ряда распределения, различают атрибутивные и вариационные ряды распределения.

Атрибутивными называют ряды распределения, построенные по качественным признакам, т.е. признакам, не имеющим числового выражения (по полу, профессии, образованию, должности, возрасту, стажу и т.д.).

Вариационными рядами называют ряды распределения, построенные по количественному признаку.

В зависимости от характера вариации признака различают дискретные и интервальные ряды.

Дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Например, распределение семей по числу детей (чел.).

Построение интервальных вариационных рядов целесообразно прежде всего при непрерывной вариации признака, а также если дискретная вариация проявляется в широких пределах, т.е. число вариантов прерывного признака достаточно велико. Например, дискретный ряд распределения студентов группы по росту.

Любой вариационный ряд состоит из двух элементов: вариантов и частот. Вариантами (х) называются отдельные значения признака, которые он принимает в вариационном ряду, т.е. конкретное значение варьирующего признака. Частотами (f) называются численности отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, которые показывают, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, ее объем. Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Рассчитываются путем деления частоты каждого интервала на их общую сумму. Соответственно сумма частостей равна 1, или 100%.

Полученный вариационный ряд оформляют в виде таблицы, где в первой графе указывают варианты (интервалы) значений признака, а в следующих графах – частоту (частость).

Способы построения вариационного ряда для дискретных и непрерывных признаков различны.

Если дискретная вариация проявляется в широких пределах, то как и при непрерывной вариации, строят интервальные вариационные ряды. При группировке единиц однокачественной совокупности можно использовать равные интервалы.

Если вариационный ряд представлен неравными и нтервалами, то частоты в отдельных интервалах непосредственно несопоставимы, так как они зависят от ширины интервала. Для сравнения частот в разных интервалах рассчитывают показатели абсолютной и относительной плотности распределения.

Абсолютная плотность h – это отношение частоты к величине интервала, а относительная плотность 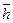- это отношение частости к величине интервала.

Ряд распределения, состоящий из двух граф (варианты и частоты), иногда дополняется другими графами, необходимыми для вычисления отдельных статистических показателей или для более отчетливого выражения характера вариации изучаемого признака. Достаточно часто в ряд вводится графа накопленные частоты (S), которые исчисляются путем последовательного прибавления к частоте первого интервала частот последующих интервалов.

Главное предназначение рядов распределения – изучение вариации признаков.

Для графического изображения дискретных рядов используют полигон распределения, который представляет собой замкнутый многоугольник, абсциссами вершин которого являются значения варьирующего признака, а ординатами – соответствующие им частоты или частости.

Гистограмма(гр. histos – ткань, строение) применяется для изображения интервального вариационного ряда, который представляют собой столбики с основаниями, равными ширине интервалов, и высотой, соответствующей частоте. В случае неравенства интервалов гистограмма строится не по частотам, а по плотности распределения.

Гистограмма может быть преобразована в полигон распределения, если найти середины сторон прямоугольников и затем эти точки соединить прямыми линиями.

В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята).

Тема 3. ТАБЛИЧНОЕ И ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СТАТИСТИЧЕСКИХ ДАННЫХ, ВЫБОРОЧНОЕ НАБЛЮДЕНИЕ