Производство в долгосрочном периоде: отдача от масштаба производства

Как уже отмечалось в предыдущем параграфе, расширение производства в долгосрочном периоде происходит при увеличении всех видов ресурсов. В этом случае увеличиваются масштабы производства, при этом отдача от масштаба может быть как постоянной, так и меняющейся (убывающей, возрастающей).

Пусть первоначальное соотношение между выпуском и применяемыми ресурсами описывается производственной функцией

Qo = f(K,L)

Если мы увеличим объемы применяемых ресурсов (масштаб производства) в n раз, то новый объем выпуска, очевидно, соста­вит:

Q₁₌ f(nK,nL)

Если в результате выпуск увеличится также в n раз (Q₁=nQo), то наблюдается постоянная отдача от масштаба.

Если выпуск увеличится менее чем в n раз (Q₁ < nQ_o), то имеет место убывающая отдача от масштаба.

Если выпуск увеличится более чем в n раз (Q₁> nQo), то имеет место возрастающая отдача от масштаба.

Для однородной производственной функции данная закономерность имеет вид:

Q₁(nL,nK)=n^tQ₀(L,K) (7.9)

Производственная функция называется однородной, если при увеличении количества всех производствен­ных ресурсов в n-раз выпуск увеличивается в n^t в соответствии с формулой(7.9).

Показатель t характеризует степень однородностифункции. Если же равенство (7.9) для данной производственной функции не выполняется, то такая производственная функция называется неоднородной.

Степень однородности может использоваться для характери­стики типа отдачи от масштаба.

Если t = 1, то отдача от масштаба постоянна, а производ­ственная функция в этом случае обычно называется линейно-однородной;

если t < 1, имеет место убывающаяотдача от масштаба;

если t > 1 — возрастающаяотдача от масштаба.

Для производственной функции Кобба-Дугласа: Q= L^aK ^b , отдача от масштаба будет определяться суммой коэффициентов эластичности:

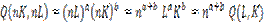(7.10)

если а+b=1, мы имеем постоянную отдачу от масштаба,

если a+b>1, наблюдается возрастающая отдача от масштаба,

если a+b<1 — убывающая отдача от масштаба

Для однородной производственной функции отдача от масштаба может быть представлена графически. Показателем отдачи может служить расстояние вдоль луча, проведенного из начала координат, между изоквантами, представляющими кратные Q объемы выпуска — Q, 2Q, dQ и т.д. В случае неодно­родности производственной функции оценка отдачи от масштаба и ее графическое отображение могут представить значительные трудности.

Постоянная отдача от масштаба наблюдается в тех производствах, где ресурсы в техническом смысле однородны и их количества можно изменять пропорционально. В таких производствах увеличение выпуска может быть достигнуто путем кратного увеличения объема применения всех производственных ресурсов. Например удвоение затрат труда и капитала будет сопровождаться удвоением выпуска.

Убывающая отдача, как правило, связана с ограниченными возможностями управления крупным производством. Кон­центрация управления (на неизменной технической базе) сверх определенного предела ведет к нарушению координации потоков ресурсы—выпуск.

Возрастающая отдача имеет место, как правило, на узкоспециализированных предприятиях, где применяются наиболее прогрессивные технологии. Если предприятие использует современные и дорогостоящие производственные фонды, труд высококвалифицирванных специалистов, применяет современные методы организации производства, то объем выпуска опережает затраты на ресурсы. Однако рост отдачи от масштаба имеет количественные ограничения. Эти ограничения связаны с постепенной потерей управляемости бизнес-процессами, бюрократизацией управленческого аппарата, понижением эффективности организации производства.

Определение оптимальной комбинации ресурсов предприятием тождественно определению потребительского оптимума. Оптимум потребителя определялся нами как равенство предельной нормы замещения благ (MRS) соотношению их цен. Подобным же образом оптимум предприятия определяется как равенство предельной нормы техниче­ского замещения ресурсов К и L соотношению их цен:

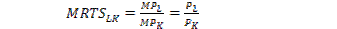(7.11)

где P_L -цена единицы труда;

P_{K –} цена единицы капитала

Следует отметить, что соотношение цен ресурсов отражает норму по которой предприятие замещает ресурсы на рынке, а соотношение предельных продуктов этого же равенства является характеристикой нормы замещения в производстве. Пока равновесие не достигнуто, предприятие может улучшить свое положение, изменив структуру используемых ресурсов Например, если производительность труда выше, чем у капитала, предприниматель расширяет спрос на труд и через какое-то время равновесие восстанавливается (относительно дорогой труд будет вытесняться относительно дешевым капиталом) :

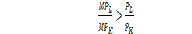
Условие оптимального сочетания ресурсов можно переинтерпретировать следующим образом. В таком виде оно получило название эквимаржинального принципа, то есть равенства предельной отдачи на труд и капитал в расчете на единицу цены. Таким образом, равновесие наступает при условии, когда последние денежные средства приносят одинаковую отдачу как от вложений в капитал, так и от вложений в труд.

Вопросы для самоконтроля

1 Назовите сущностные признаки фирмы для технологической парадигмы?

2 Сформулируйте основные допущения к неоклассической модели фирмы?

3 Каковы сущностные признаки фирмы для институциональной парадигмы?

4 В чем состоят различия между фирмой и рынком?

5 Какие элементы включаются в состав трансакционных затрат?

6 Как в трансакционной теории определяются оптимальные размеры фирмы?

7 Что такое производственная функция и каковы ее основные характеристики?

8 Что означает экономическая и технологическая эффективность производства?

9 Что такое изокванта и каковы ее основные характеристики?

10 Какими характеристиками обладают изокванты для разных видов производственной функции?

11 Что такое стадии производства? Какую роль в экономическом анализе играет вторая стадия производства?

12 Каким образом соотносятся функции общего, среднего и предельного продуктов фактора производства?

13 Что означает возрастающая и убывающая отдача от масштаба производства?

14 Что означает экономия от масштаба производства и чем она обусловлена?

15 Как определяются условия оптимального выпуска для фирмы?