Пороговая передаточная функция
Функции активации.
Линейная передаточная функция
Сигнал на выходе нейрона линейно связан со взвешенной суммой сигналов на его входе.
f(x) = tx
, где t - параметр функции. В искусственных нейронных сетях со слоистой структурой нейроны с передаточными функциями такого типа, как правило, составляют входной слой. Кроме простой линейной функции могут быть использованы её модификации. Например полулинейная функция (если её аргумент меньше нуля, то она равна нулю, а в остальных случаях, ведет себя как линейная) или шаговая (линейная функция с насыщением), которую можно выразить формулой
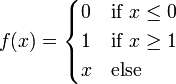
При этом возможен сдвиг функции по обеим осям (как изображено на рисунке).
Недостатками шаговой и полулинейной активационных функций относительно линейной можно назвать то, что они не являются дифференцируемыми на всей числовой оси, а значит не могут быть использованы при обучении по некоторым алгоритмам.
Пороговая передаточная функция
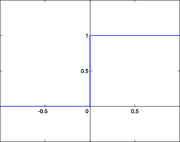
Другое название - Функция Хевисайда. Представляет собой перепад. До тех пор пока взвешенный сигнал на входе нейрона не достигает некоторого уровня T — сигнал на выходе равен нулю. Как только сигнал на входе нейрона превышает указанный уровень — выходной сигнал скачкообразно изменяется на единицу. Самый первый представитель слоистых искусственных нейронных сетей — перцептрон[11] состоял исключительно из нейронов такого типа[5]. Математическая запись этой функции выглядит так:
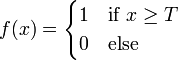
Здесь T = − w0x0 — сдвиг функции активации относительно горизонтальной оси, соответственно под x следует понимать взвешенную сумму сигналов на входах нейрона без учёта этого слагаемого. Ввиду того, что данная функция не является дифференцируемой на всей оси абсцисс, её нельзя использовать в сетях, обучающихся по алгоритму обратного распространения ошибки и другим алгоритмам, требующим дифференцируемости передаточной функции.
Дата добавления: 2016-03-30; просмотров: 1317;
