Методи розрахунку розмірних ланцюгів
Розв’язувати пряму і зворотну задачі можна різними методами:
1) метод повної взаємозамінності (метод розрахунку на максимум-мінімум);
2) ймовірнісний метод (метод неповної взаємозамінності);
3) метод регулювання;
4) метод пригону;
5) метод групової взаємозамінності.
5. Рішення прямої і зворотної задач методом повної взаємозамінності
Розглянемо основні властивості і порядок розрахунку розмірних ланцюгів з паралельними ланками за методом повної взаємозамінності.
1). Розв’язання зворотної задачі має такий вигляд.
Визначається номінальний розмір замикальної ланки
АΔ = 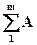 i зб -
i зб - 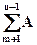 i зм,
i зм,
тобто номінальний розмір замикальної ланки дорівнює різниці суми номінальних розмірів збільшувальних А i зб і зменшувальних А i зм ланок.
Визначаються граничні відхили розміру замикальної ланки
ESАΔ = 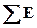 SAi зб -
SAi зб - 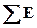 IAi зм;
IAi зм;
EIАΔ = 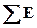 IAi зб -
IAi зб - 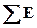 SAi зм.
SAi зм.
Визначається допуск замикальної ланки
TАΔ = 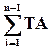 i,
i,
тобто допуск замикальної ланки дорівнює сумі абсолютних значень допусків складових ланок.
З цього рівняння можна зробити висновок: чим більше деталей у складальному ланцюзі, тим з більшою точністю треба обробляти їх для забезпечення заданої точності складання.
2). Розв’язання прямої задачі виконується у такій послідовності.
Визначають допуск замикальної ланки за заданими граничними відхилами цієї ланки
ТА 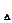 = ЕSА
= ЕSА 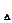 - ЕІА
- ЕІА 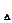 = А
= А 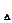 max - А
max - А 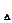 min .
min .
Визначають середній квалітет розмірного ланцюга за середнім числом одиниць допуску
k =  ,
,
де 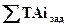 - сума допусків складових ланок, допуски яких задані;
- сума допусків складових ланок, допуски яких задані;
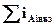 - сума одиниць допусків складових ланок, допуски яких визначаються.
- сума одиниць допусків складових ланок, допуски яких визначаються.
При цьому квалітет визначають за значенням числа одиниць допуску і вибирають за таблицями.
Визначають граничні відхили і допуски складових ланок.
Визначають суму допусків усіх складових ланок 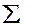 ТАi (з ланками із заданими допусками).
ТАi (з ланками із заданими допусками).
Порівнюють допуск замикальної ланки з визначеною сумою допусків усіх складових ланок. Якщо ТА 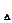 =
=  , то допуски усіх ланок назначені правильно. Коли ТА
, то допуски усіх ланок назначені правильно. Коли ТА 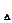
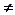
 , то допуск і граничні відхили однієї з ланок (корегуючої) слід визначати додатково.
, то допуск і граничні відхили однієї з ланок (корегуючої) слід визначати додатково.
Перевіряють правильність розрахунку розмірного ланцюга за формулою
ТА 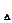 =
= 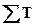 Аi.
Аi.
6. Розрахунок розмірних ланцюгів ймовірнісним методом
Цей метод застосовують, якщо при розв’язанні прямої задачі економічно доцільно призначати на складові ланки ланцюгів більш широкі допуски, ніж ті, що одержують при розв’язанні методом повної взаємозамінності.
Основою цього методу є теореми математичної статистики, що встановлюють властивості дисперсії.
Замикальна ланка розмірних ланцюгів є випадковою величиною, що дорівнює сумі незалежних випадкових змінних, тобто є сумою незалежних відхилів складових ланок ланцюгів.
Відношення між допусками замикальної ланки і складовими ланками має вигляд:
ІТА 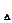 =
= 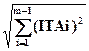 .
.
Ця формула справедлива тільки тоді, якщо похибки замикальної ланки підпорядковані закону нормального розподілу. Прийнято вважати, що розподіл похибок замикальної ланки в розмірних ланцюгах з числом ланок більше п’яти є нормальним.
Для визначення граничних відхилів в розрахунок вводять середній відхил, тобто координату середини поля допуску ( Em):
Е 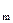 Аі =
Аі = 
де ESAi і ЕІАi підставляються у формулу зі своїми знаками.
Тоді граничні відхили i-тої ланки
ЕSAі = 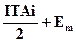 Aі;
Aі;
ЕІАі = Е 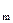 Аі -
Аі - 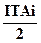 .
.
Аналогічні формули для замикальної ланки:
ЕSA 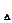 = Е
= Е 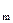 А
А 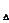 -
- 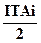 .
.
Співвідношення між середнім відхилом замикальної ланки і складових ланок має вигляд:
Е 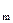 А
А 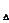 =
=  Е
Е 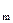 Аізб -
Аізб - 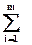 Е
Е 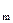 Аізм.
Аізм.
При розв’язанні прямої задачі із застосуванням положень теорії ймовірності визначають число одиниць допуску за формулою
k = 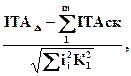
де К1 – коефіцієнт відносного розсіювання розмірів:
К1 = 6σі/Тj,
де Тj – поле розсіювання Аі.
Відношення числа одиниць допуску k, визначених за методом повної і неповної взаємозамінності, характеризує зміну точності розмірних ланок.
Дата добавления: 2016-03-27; просмотров: 1241;
