Расчет сепарации газа
Максимальное выделение из нефти углеводородов и сопутствующих газов наступает при равновесном состоянии между нефтью и газом, т. е. когда давление и температура в каждой точке газа и нефти постоянные. Пока такого состояния нет, система не может находиться в равновесии. Незначительное изменение давления или температуры в какой-либо точке (или зоне) системы, находящейся в равновесии, приведет к нарушению равновесного состояния, которое может продолжаться до тех пор, пока указанное изменение давления или температуры не распространится на весь объем жидкой и газовой фаз. После этого давление и температура в системе станут опять постоянными по всему объему обеих фаз и наступит опять равновесное состояние. Но оно будет отличным от первого как по температуре или давлению, так и по количеству и составу газовой фазы. Продолжительность установления равновесного состояния и перехода от одного равновесного состояния в другое зависят от степени термостатирования системы, от величины изменения температуры и давления, от массы нефти и газа и от соотношения их масс.
Строго говоря, равновесного состояния между газом и нефтью в природе не может быть. Оно может очень приближаться к нему, беспрерывно нарушаться вследствие изменения температуры или давления в какой-либо точке (или зоне) системы и устанавливаться вновь. Поэтому систему, в которой быстро чередуются друг за другом равновесные состояния при бесконечно малых изменениях давления и температуры, называют также равновесной.
Приведенные рассуждения относятся к условиям, в которых нефть и газ находятся в неподвижном состоянии. Встряхивание нефти ускоряет процесс приведения системы в равновесное состояние. В промысловых газосепараторах нефть и газ поступают непрерывно, а иногда пульсирующим потоком, с температурой и давлением несколько отличными, чем установленными в газосепараторе, и вывод их происходит относительно быстро. Эти явления, а также различное влияние внешней среды (солнечные лучи, ветер и др.) не способствуют установлению равновесного состояния системы нефть–газ в газосепараторе. Вследствие этого углеводороды и сопутствующие газы не могут полностью выделиться из нефти даже при температуре газовой фазы выше температуры нефти, что имеет место в летнее время под влиянием солнечных лучей. Поэтому в нефти могут оставаться больше, чем это следует по закону межфазного равновесия, углеводородов, азота, обладающих относительно высоким давлением насыщенных паров.
Влияние неравновесных условий на величину газового фактора и состав газа при сепарации должно зависеть от условий сепарации и состава нефти и особенно от количества в ней азота.
В практике сбора и обработки нефти и газа приходится решать задачи распределения углеводородов между газом и нефтью, например при сепарации газа, испарении и нагреве нефти, извлечении углеводородов из нефти и газа, конденсации газа и пр. Это может быть осуществлено путем расчета или экспериментально. При расчете исходят из предположения, что система газ–нефть находится в равновесных условиях при заданных давлении и температуре. Это предположение может привести иногда к значительным расхождениям по составу газа, особенно если содержание азота в одной из фаз составляет 30% мольных и более.
Для расчета процессов, связанных с выделением из нефти головных углеводородов и из газа тяжелой их части (сепарация газа, испарение и кипение нефти), необходимо знать константы равновесия k между газовой и нефтяной фазами для каждого углеводорода, определяемые давлением, температурой и составом смеси. Решением системы уравнений устанавливают распределение углеводородов между газом и жидкостью. В общем случае, если система состоит из m компонентов, то количество неизвестных в расчете составит 2m + 2, из них m значений х (мольные доли каждого компонента в нефти) и m значений у (мольные доли компонентов в газе), а также мольные доли всех компонентов, содержащихся в нефти L и в газе V.
Пусть дано общее количество молей в нефти n. Нефть подвергается испарению. Согласно закону Дальтона сумма парциальных давлений 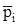 , всех компонентов газа равна общему давлению р, т. е.
, всех компонентов газа равна общему давлению р, т. е.
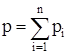 , (3.18)
, (3.18)
и объемная или мольная доля компонента i в газовой фазе равна парциальному давлению компонента рi, деленному на общее давление газовой фазы р, т.е.
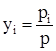 . (3.19)
. (3.19)
Кроме того, согласно закону Рауля парциальное давление компонента i в нефти 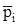 , равно давлению насыщенного пара
, равно давлению насыщенного пара 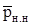 этого компонента, умноженному на его мольную долю в нефти xi, т. е.
этого компонента, умноженному на его мольную долю в нефти xi, т. е.
 . (3.20)
. (3.20)
Если система нефть–газ находится в равновесии, то парциальное давление компонента в газовой фазе должно равняться парциальному давлению этого же компонента в нефтяной фазе, т. е.
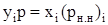 , (3.21)
, (3.21)
или
 , (3.22)
, (3.22)
где ki – коэффициент распределения компонента i при давлении р и температуре Т.
Если общее количество молей смеси n распределилось между газом и нефтью и система нефть–газ находится в равновесии, то
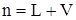 . (3.23)
. (3.23)
Мольная доля компонента i в смеси, очевидно, будет
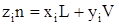 . (3.24)
. (3.24)
Так как xi, уi, и zi мольные доли, то представляется возможным написать три соотношения
 . (3.25)
. (3.25)
Для 1 кмоля смеси n=1. В этом случае
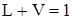 , (2.26)
, (2.26)
поэтому материальный баланс по каждому компоненту будет
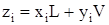 . (3.27)
. (3.27)
Заменив yi из (3.27), получим
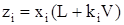 . (3.28)
. (3.28)
Разделив обе части этого уравнения на 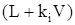 получим
получим
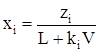 . (3.29)
. (3.29)
Затем, разделив числитель и знаменатель правой части последнего уравнения на V, получим уравнение концентрации любого компонента в нефти при заданных давлении и температуре
 . (3.30)
. (3.30)
Согласно (3.25) имеем
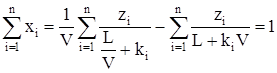 . (3.31)
. (3.31)
или
 . (3.32)
. (3.32)
Если в уравнении (3.27) заменить хi из (3.22) и решить это уравнение относительно yi, то будем иметь
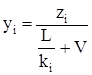 . (3.33)
. (3.33)
Согласно (3.25) имеем
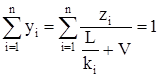 ,
,
откуда
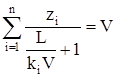 . (3.34)
. (3.34)
Эти уравнения справедливы для систем: нефть–газ, конденсат–газ, сжиженные углеводороды–газ и др.
В области абсолютных давлений ниже 0,3 – 0,4 МПа легкие углеводороды и сопутствующие им газы ведут себя как идеальный газ. На них распространяются законы Рауля и Дальтона. В этом случае справедлива зависимость
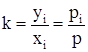 , (3.35)
, (3.35)
где р – общее давление; рi – парциальное давление паров компонента.
При абсолютных давлениях до 5 aт и с некоторым допущением до 10 ат для определения k можно пользоваться номограммой Де-Пристера (рис.3.19).
При давлениях выше 1 МПа, а в отдельных случаях при давлениях до 2 МПа уже нельзя пренебрегать влиянием состава смеси. Коэффициенты распределения при этом определяют методами, разработанными за последние 12 лет. Эти методы основаны на понятии давления сходимости (схождения). Давлением сходимости называют специфическое для данных температур и состава давление, при котором коэффициенты распределения k для всех компонентов нефти становятся одинаковыми и равными единице. Это имеет место при температуре, превышающей критическую температуру наиболее легкого компонента данной смеси.
Если температура, при которой даны коэффициенты распределения, является критической температурой смеси, то давление сходимости будет критическим давлением. При всех температурах, отличающихся от критической температуры, сходимость величин k является только "кажущейся". При некотором давлении, меньшем давления сходимости, система будет находиться в состоянии точки росы или точки начала парообразования, а при условиях, соответствующих точке кажущейся сходимости, система должна существовать в однофазном состоянии. Так как коэффициенты распределения в однофазном состоянии вещества не определены, то их находят экстраполяцией действительных величин, которые, по-видимому, сходятся в единице.
На рис. 3.20 – 3.32 приведены графики коэффициентов распределения углеводородов от метана до декана, а также азота при давлении сходимости рабс = 350 aт, а на рис. 3.33 и 3.34 для сероводорода и углекислоты при давлении сходимости рабс = 280 aт. Эти графики могут быть использованы для расчета сепарации при давлениях до 35 aт и меньше, а также для большинства природных углеводородных смесей.
Коэффициент распределения фракции гептаны+ может быть получен из рис.3.35 или принят эквивалентным значению октана или нонана из приведенных диаграмм.

Рис. 3.19.Номограмма Де-Пристера для определения коэффициентов распределения

Рис.3.20. Коэффициенты распределения для метана: давление сходимости 350 aт
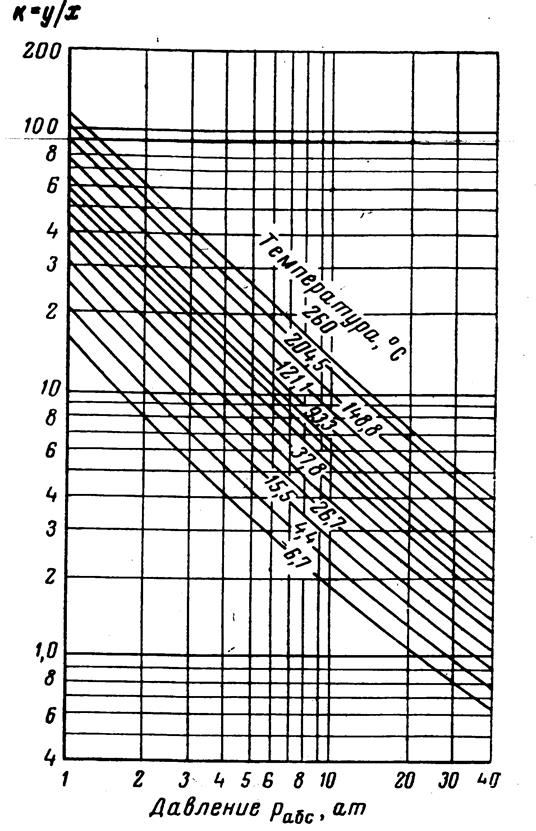
Рис.3.21. Коэффициенты распределения для этана: давление сходимости 350 aт
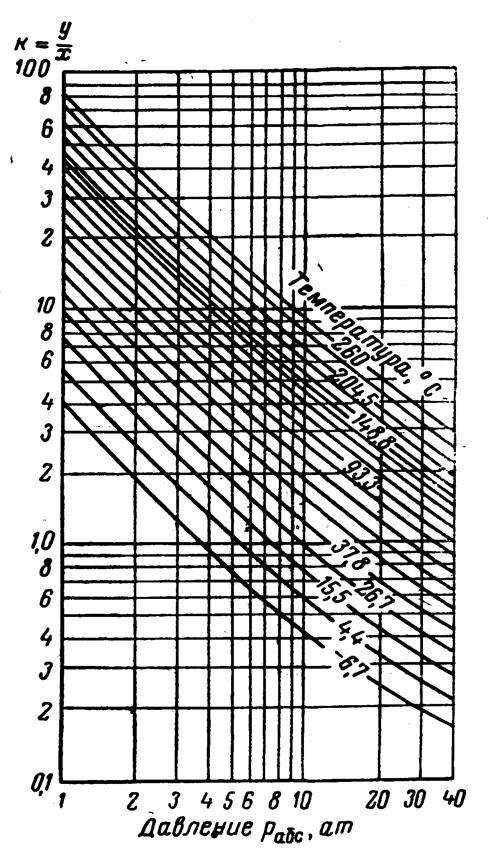
Рис.3.22. Коэффициенты распределения для пропана: давление сходимости 350 aт.
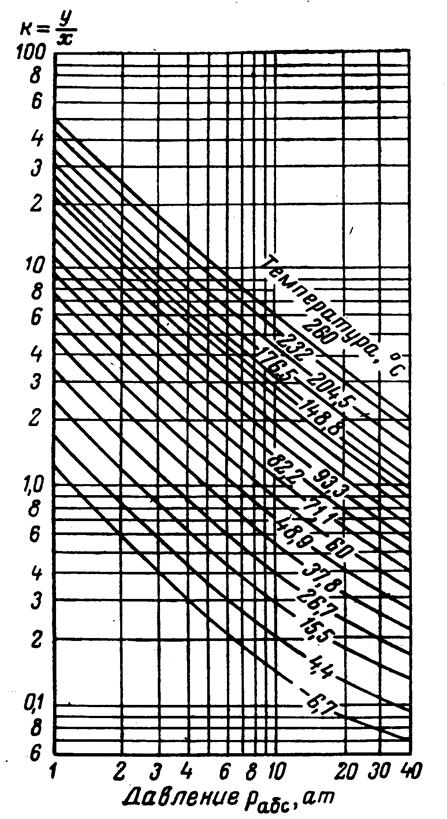
Рис.3.23. Коэффициенты распределения для нормального бутана: давление сходимости 350 aт
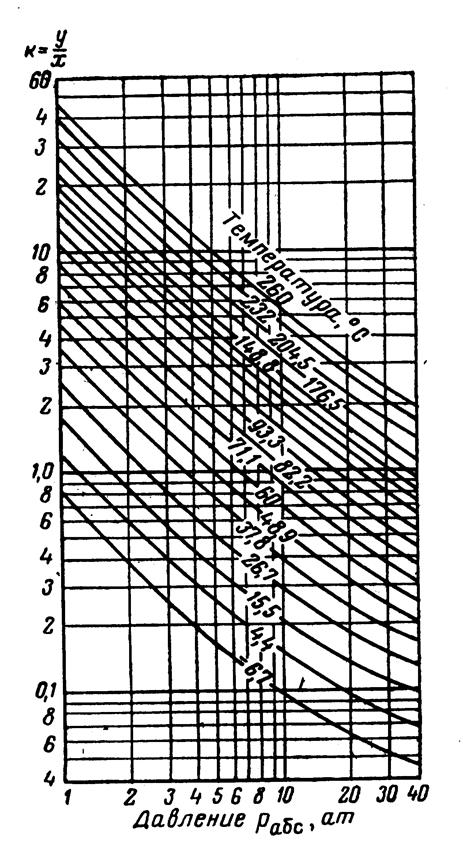
Рис.3.24. Коэффициенты распределения для изобутана: давление сходимости 350 aт
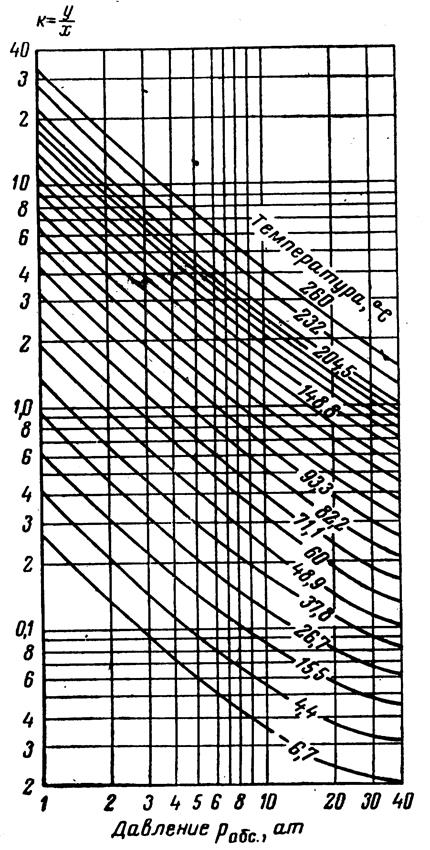
Рис.3.25. Коэффициенты распределения для изопентана: давление сходимости 350 aт

Рис.3.26. Коэффициенты распределения для нормального пентана: давление сходимости 350 aт
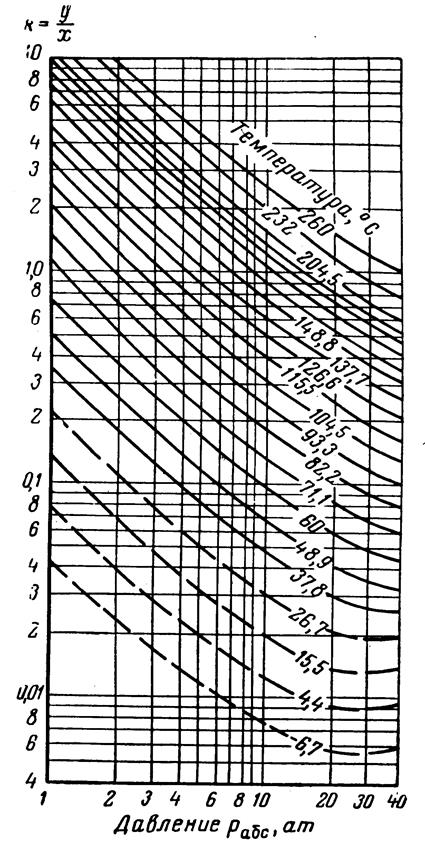
Рис.3.27. Коэффициенты распределения для гексана: давление сходимости 350 aт
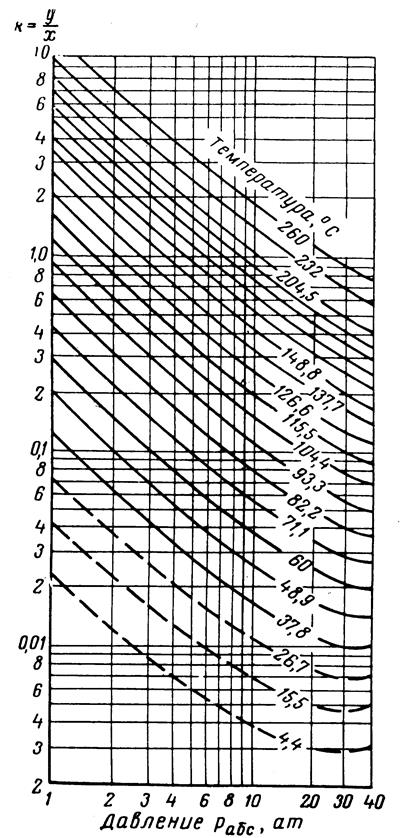
Рис.3.28. Коэффициенты распределения для гептана: давление сходимости 350 aт

Рис.3.29. Коэффициенты распределения для октана: давление сходимости 350 aт
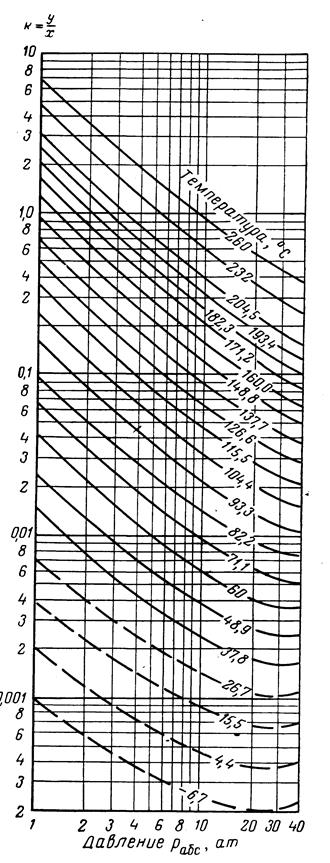
Рис.3.30. Коэффициенты распределения для нонана: давление сходимости: 350 ат
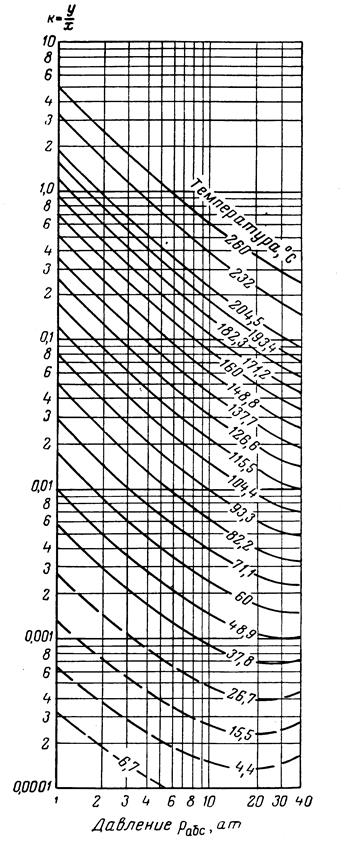
Рис.3.31. Коэффициенты распределения для декана: давление сходимости 350 ат
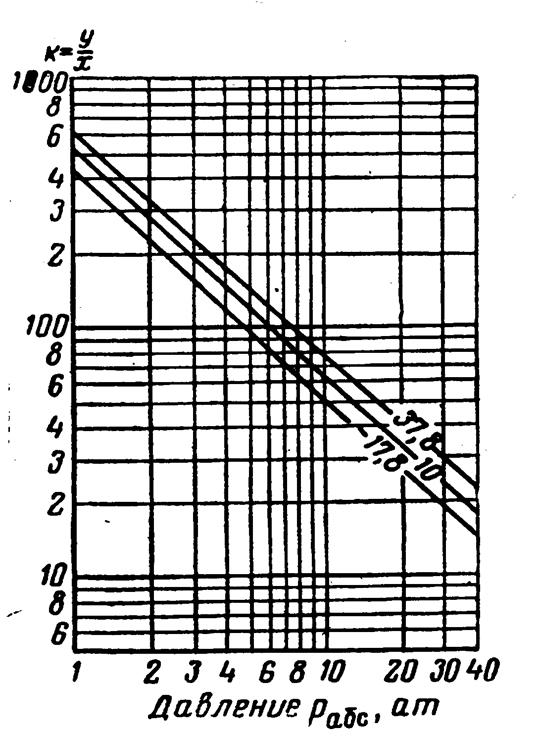
Рис.3.32. Коэффициенты распределения для азота: давление сходимости 350 ат
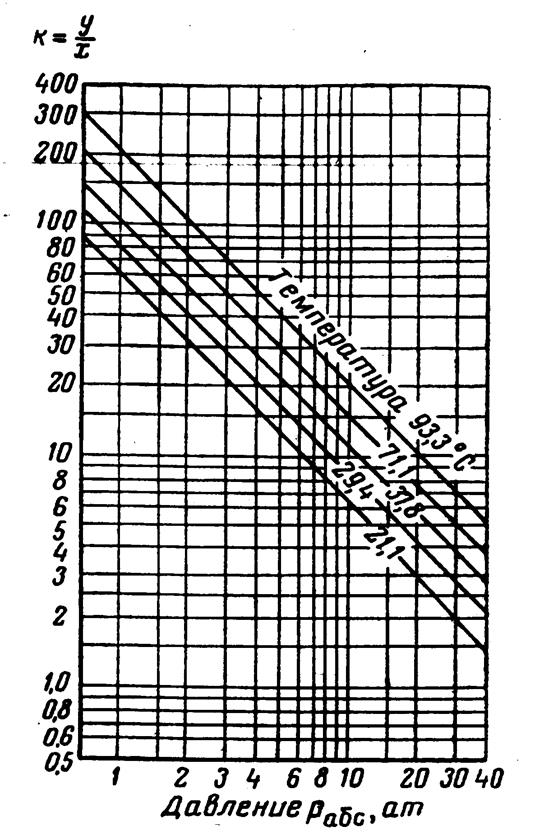
Рис.3.33. Коэффициенты распределения для углекислого газа: давление сходимости 280 aт

Рис.3.34. Коэффициенты распределения для сероводорода: давление сходимости 280 ат
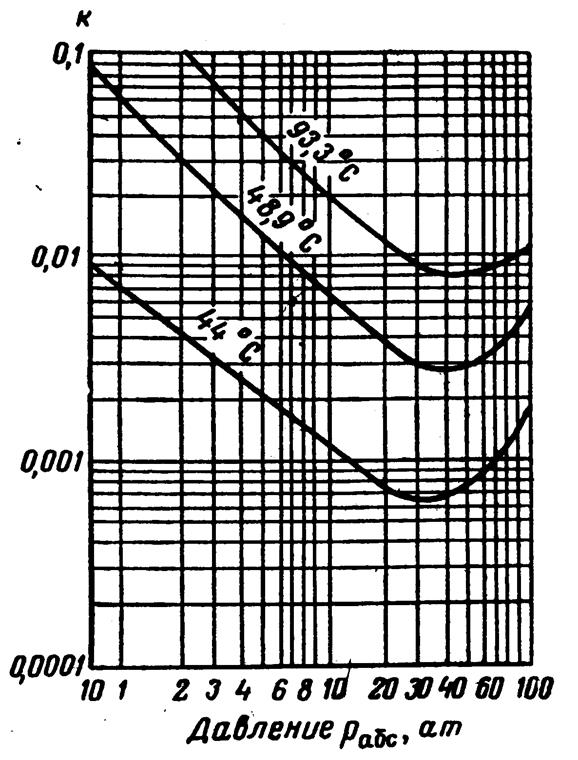
Рис.3.35. Коэффициенты распределения для фракции гептаны + для сырой нефти: давление сходимости по Кацу и Хачмату
Дата добавления: 2016-03-27; просмотров: 17747;
