Методика и техника эксперимента. Электрический ток, проходящий по любому контуру, создает магнитный поток Ф, пронизывающий этот контур
Электрический ток, проходящий по любому контуру, создает магнитный поток Ф, пронизывающий этот контур. В соответствии с законом Био-Савара-Лапласа магнитная индукция В пропорциональна силе тока, вызвавшего поле. Следовательно, и магнитный поток через контур пропорционален силе тока в нем :
Ф = L·I. (5.17)
Коэффициент пропорциональности L называют индуктивностью данного контура, которая зависит то геометрии контура (т.е. от его формы и размеров), а также от магнитных свойств окружающей контур среды. Для длинного соленоида или тороида индуктивность может быть рассчитана по формуле:
L = µ0 ·µ·n2 ·V, (5.18)
где n – число витков на единицу длины ; V – объем соленоида или тороида; µ– магнитная проницаемость материала сердечника; µ0 – магнитная постоянная.
Если сердечник изготовлен из ферромагнитного материала (железо, никель, кобальт и сплавы, содержащие эти элементы), для которого магнитная проницаемость зависит от напряженности магнитного поля, то индуктивность такого соленоида или тороида не постоянна. Она зависит от силы тока, проходящего по данной катушке.
Единицей измерения индуктивности в системе СИ является генри (Гн). (1 Гн – индуктивность такого контура, у которого при силе тока в нем 1 А возникает сцепленный с ним магнитный поток в 1 Вебер (Вб)).
Если по катушке индуктивности проходит изменяющийся со временем ток, то в нем возникает ЭДС самоиндукции, препятствующая изменению тока.
 .
.
Катушка индуктивности, включенная в цепь переменного тока, оказывает сопротивление прохождению тока. Величина индуктивного сопротивления пропорциональна частоте переменного тока и индуктивности катушки:
ХL = ω·L. (5.19)
 Рассмотрим цепь, содержащую активное сопротивление R и катушку индуктивности L, подключенные к источнику переменного тока.
Рассмотрим цепь, содержащую активное сопротивление R и катушку индуктивности L, подключенные к источнику переменного тока.
Пусть сила тока в цепи меняется по закону
I = Im·sin ωt. (5.20)
Падение напряжения на активном сопротивлении U = I·R по фазе совпадает с колебаниями тока в цепи. Падение напряжения на индуктивности будет равно ЭДС самоиндукции с обратным знаком:
UL = – E S = L  = Lω Im·cos ωt = Lω Im·sin (ωt +
= Lω Im·cos ωt = Lω Im·sin (ωt + 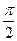 ). (5.21)
). (5.21)
Сравнивая выражения (5.20) и (5.21), мы видим, что колебания напряжения на катушке индуктивности опережают по фазе колебания тока на 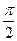 . Векторная диаграмма напряжений для рассматриваемого случая представлена ниже:
. Векторная диаграмма напряжений для рассматриваемого случая представлена ниже:


Из этой диаграммы видно, что активное и индуктивное сопротивления цепи складываются геометрически. Полное сопротивление цепи:
Z = 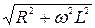 . (5.22)
. (5.22)
 Индуктивность катушки можно измерить при помощи различных мостовых схем. В этой работе применяется мост Максвелла, принципиальная схема которого изображена ниже:
Индуктивность катушки можно измерить при помощи различных мостовых схем. В этой работе применяется мост Максвелла, принципиальная схема которого изображена ниже:


В плечо моста АС включена эталонная катушка индуктивности с известными значениями R и L, указанными на катушке. Плечо СВ содержит катушку, сопротивление которой известно (его значение Rx указанно на панели установки), а индуктивность Lx измеряется в данной работе. Два других плеча АD и DВ представлены реостатом. Их сопротивления r1 и r2 могут изменяться при перемещении движка реостата D.
В одну диагональ моста включается источник переменного напряжения (напряжение городской сети с помощью трансформатора понижается до 12 В). В другую диагональ включается гальванометр. Мост находится в равновесии, если ток через гальванометр не проходит.
Для вывода условий равновесия моста применим второй закон Кирхгофа к контурам АВMNA и АСВMNA:
I1r1 – I2r2= 0, (5.23)
I1· 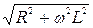 – I2·
– I2· 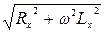 = 0. (5.24)
= 0. (5.24)
Из уравнений (5.23) и (5.24) следует:
 . (5.25)
. (5.25)
Поскольку реостат изготовлен из однородной проволоки, равномерно навитой на цилиндрический сердечник, то
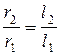 , (5.26)
, (5.26)
где l1 и l2 – расстояния от движка реостата D до его концов. Тогда равенство (5.25) перепишется так:
 . (5.27)
. (5.27)
Отсюда:
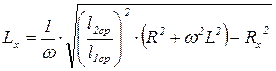 . (5.28)
. (5.28)
Эта формула используется в данной работе для определения индуктивности катушки. ω – циклическая частота переменного тока, она связанна с частотой соотношением ω = 2πν. В данной работе мы используем переменный ток частотой 50 Гц, следовательно, ω =314 с-1.
Дата добавления: 2016-02-16; просмотров: 735;
