Методика и техника эксперимента. Работа посвящена практически важному вопросу об использовании энергии источника тока

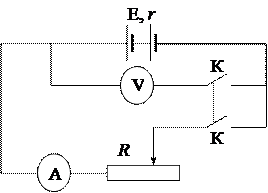Работа посвящена практически важному вопросу об использовании энергии источника тока. Рассмотрим электрическую цепь, содержащую источник тока с электродвижущей силой Е и внутренним сопротивлением r, замкнутый на реостат, с помощью которого можно изменять внешнее сопротивление R (сопротивление нагрузки). Сила тока в цепи I измеряется амперметром, напряжение на внешнем участке цепи U – вольтметром.

Зависимость силы тока в цепи I от внешнего сопротивления R определяется с помощью закона Ома для полной цепи

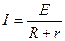. (2.2)

С помощью закона Ома для внешнего участка цепи

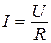(2.3)

нетрудно выразить зависимость напряжения U от силы тока I. Для этого из уравнения (2.3) получим , а из (1) .

Из последнего выражения получим искомую зависимость

. (2.4)

Нетрудно видеть, что это линейная зависимость вида . Примерный вид этой зависимости представлен на графике.

Из (2.2) видно, что сила тока обращается в нуль при бесконечно большом внешнем сопротивлении 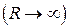, то есть в случае разомкнутой цепи. Тогда напряжение на зажимах источника равно ЭДС. Графически ЭДС представляет отрезок, отсекаемый прямой на оси ординат.

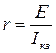. (2.5)

Мощность, выделяющаяся на сопротивлении нагрузки, является полезной мощностью источника тока, по закону Джоуля–Ленца, она равна . Мощность, выделяющаяся на внутреннем сопротивлении, представляет собой тепловые потери на нагревание источника, полная мощность выделяется на суммарном сопротивлении всей цепи: .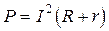

С помощью законов Ома для внешнего участка цепи и полной цепи можно выразить полезную и полную мощность через сопротивление нагрузки: 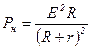, (2.6)

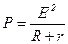, (2.7)

так и через силу тока

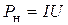, (2.8)

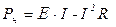, (2.8а)

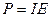. (2.9)

Полная мощность прямо пропорциональна силе тока, зависимость полезной мощности от силы тока – квадратичная и графически изображается перевернутой параболой.

Практически полезная мощность изменяется при изменении сопротивления реостата. Выясним, какую следует установить нагрузку для выделения максимальной полезной мощности. Для этого решим задачу на экстремум функции. Продифференцируем выражение (2.6) по переменной R и производную приравняем к нулю:

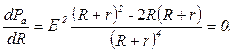
Откуда получаем , то есть мощность, выделяемая во внешней цепи, достигает наибольшего значения, если сопротивление во внешней цепи равно внутреннему сопротивлению источника. При этом согласно (2.2) ток в цепи составит ,

а наибольшее возможное значение полезной мощности .

При практическом использовании источников тока важна не только величина полезной мощности, но и коэффициент полезного действия (КПД):

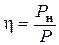. (2.10)

С помощью формул (2.8) – (2.9) это выражение можно привести к виду

. (2.11)

Очевидно, что поскольку U ≤ E, то .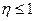

Используя (2.2), получим зависимость КПД от силы тока:

. (2.12)

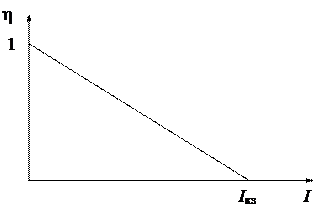КПД достигает наибольшего значения 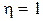в случае разомкнутой цепи и затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании.

Обратим внимание, что условие одновременного получения максимальной полезной мощности и наибольшего КПД несовместимы. Когда полезная мощность достигает максимального значения, коэффициент полезного действия источника тока . Когда же КПД близок к единице, полезная мощность мала по сравнению с максимальной мощностью, которую мог бы развить данный источник.

В силовых электрических установках важнейшим требованием является получение высокого КПД. Для этого согласно (2.12) должно выполняться неравенство:

<<1,

т.е. внутреннее сопротивление r источника должно быть мало по сравнению с сопротивлением R нагрузки. При этом мощность потерь, выделяющаяся внутри источника, оказывается малой по сравнению с полезной мощностью в нагрузке.

В случае короткого замыкания, как мы видели выше, полезная мощность равна нулю, и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. По этой причине короткое замыкание мощных источников тока (динамо машины, аккумуляторные батареи) недопустимо.