Обобщенный закон Ома
Если в проводнике создать электрическое поле и не принять мер для его поддержания, то перемещение носителей тока приведет очень быстро к тому, что напряженность внутри проводника станет равной нулю и ток прекратится. Таким образом, при наличии лишь кулоновских сил невозможно поддерживать в цепи электрический ток. Следовательно, для поддержания в цепи постоянного тока необходимо, чтобы на носители тока действовали помимо кулоновских сил иные силы, не электростатического происхождения, называемые сторонними.
Если кулоновские силы вызывают соединение разноименных зарядов, выравнивание потенциала и исчезновение поля в проводнике, то сторонние силы, наоборот вызывают разделение разноименных зарядов и поддерживают разность потенциалов на концах проводника. Сторонние силы действуют на носители тока внутри источников электрической энергии (гальванических элементов, аккумуляторов, электрических генераторов и т.п.).
В общем случае, на носитель тока q, действует сила:
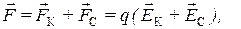
где 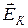 – напряженность поля кулоновских сил,
– напряженность поля кулоновских сил,  – напряженность поля сторонних сил. Тогда
– напряженность поля сторонних сил. Тогда
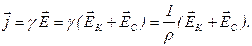
Умножим скалярно обе части равенства на dl.|dl | – длина элемента проводника. Вектор dlнаправлен по току.
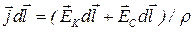 или
или 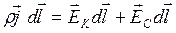
Учитывая 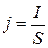 , получим
, получим 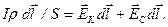
Интегрируем данное выражение по длине участка цепи 1-2:
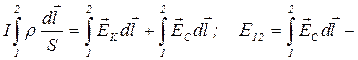
электродвижущая сила (ЭДС), действующая на участке 1-2.
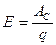 – ЭДС численно равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда.
– ЭДС численно равна работе, совершаемой сторонними силами при перемещении единичного положительного заряда.
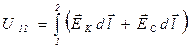 – напряжение на участке цепи 1-2.
– напряжение на участке цепи 1-2.
Напряжение – это физическая величина, численно равная суммарной работе, совершаемой кулоновскими и сторонними силами при перемещении по участку 1-2 единичного положительного заряда. Таким образом,
U12 = (φ1 – φ2) + Е12.
Сопротивление на участке 1-2:
 . Если r=const, S=const, то
. Если r=const, S=const, то  ,
,
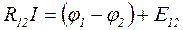 - обобщенный закон Ома или
- обобщенный закон Ома или 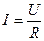 .
.
  
| Однородный участок цепи: 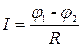 . .
| ||
R
| Неоднородный участок: 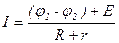 . .
| ||
 3. 3.
| Полная цепь (замкнутая):
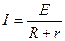 . .
|
Закон Джоуля-Ленца
При столкновении электронов (носителей тока) с атомами электроны теряют свою энергию. Эта энергия переходит в энергию хаотического движения атомов, т.е. в тепловую.
Q = I 2R t – закон Джоуля-Ленца для постоянного тока I = const.
Если ток изменяется со временем, то 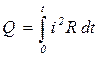 .
.
Данные формулы – интегральная форма записи закона, она выражает тепло, выделяющееся во всем проводнике.
Дифференциальная форма записи закона Джоуля-Ленца позволяет вычислить тепло, выделяющееся в различных точках проводника:
Qуд = ρ j 2, где ρ – удельное сопротивление, j – плотность тока, 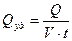 – количество тепла, выделяющееся в единицу времени в единице объема.
– количество тепла, выделяющееся в единицу времени в единице объема.
2.5. Разветвлённые цепи. Правила Кирхгофа
Расчет разветвленных цепей значительно упрощается, если пользоваться двумя правилами Кирхгофа:
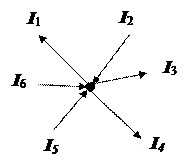 1-е правило Кирхгофа –правило узлов: алгебраическая сумма токов, сходящихся в узле, равна нулю:
1-е правило Кирхгофа –правило узлов: алгебраическая сумма токов, сходящихся в узле, равна нулю:
∑ IK = 0
-I1 + I2 – I3 – I4 + I5 + I6 = 0.
Условно считают, что токи, входящие в узел, положительные, а токи, выходящие из узла отрицательные;
2-е правило Кирхгофа–правило контуров: алгебраическая сумма произведений сил токов на участках контура на их сопротивления равна алгебраической сумме ЭДС, действующих в этом контуре:
∑IkRk = ∑Ek.
2-е правило является следствием закона Ома для неоднородных участков цепи.
Порядок расчета разветвлённых цепей
1. Произвольно выбирают направление токов во всех участках цепи. Если в результате вычислений окажется, что I >0, то направление тока выбрано правильно, если I <0, то истинное направление тока противоположно выбранному.
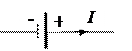 Если на участке имеется ЭДС, то можно выбрать истинное направление тока:
Если на участке имеется ЭДС, то можно выбрать истинное направление тока:
2.Выбрать направление обхода контура и строго его придерживаться (например, по часовой стрелке).
а)Произведение IR >0, если ток на данном участке совпадает с направлением обхода, и, наоборот;
б) Если ЭДС повышает потенциал в направлении обхода, то ЭДС >0
[E >0, если (–) → (+)], в противном случае ЭДС <0.
3. Составить столько уравнений, чтобы их число было равно числу искомых величин (числу токов в цепи).
Для N узлов в цепи записывают (N-1)независимых уравнений по 1-му правилу.
4.Для составления независимых уравнений по 2-му правилу Кирхгофа, каждый новый контур должен содержать хотя бы один участок, не входящий в уже рассмотренный контур.
Дата добавления: 2016-02-16; просмотров: 2226;
