Пример выполнения задания 2
Исходные данные для расчетов представлены в таблице 4.16.
Таблица 4.16 – Исходные данные
| Обозначение показателя | Наименование показателя | Значение показателя |
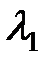
| Интенсивность использования элемента ОИ, 1/ч | 4,17 |
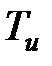
| Средняя длительность использования элемента ОИ, ч | 0,068 |
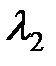
| Интенсивность отказов элемента ОИ, 10-5 1/ч | 0,6509 |
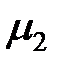
| Интенсивность восстановления элемента ОИ после отказа, 1/ч | 1,1 |
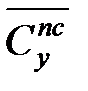
| Средняя стоимость одного часа простоя поезда, тыс. руб. | 3,393 |
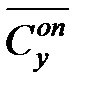
| Средняя стоимость одной дополнительной остановки поезда, тыс. руб. | 0,12746 |
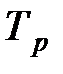
| Расчетный период, ч | |
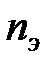
| Количество элементов ОИ |
Согласно методам теории массового обслуживания определяется параметр 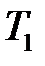 :
:
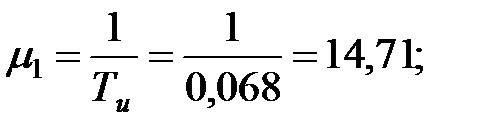
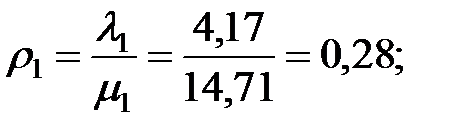
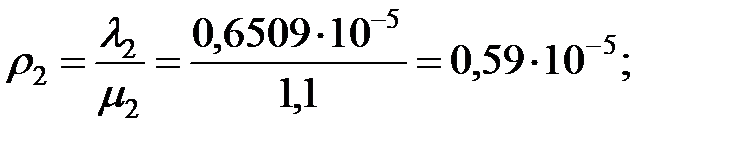
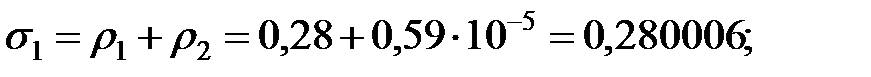
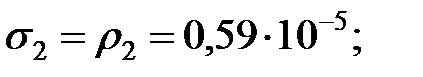
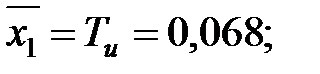
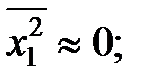
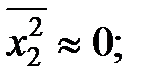
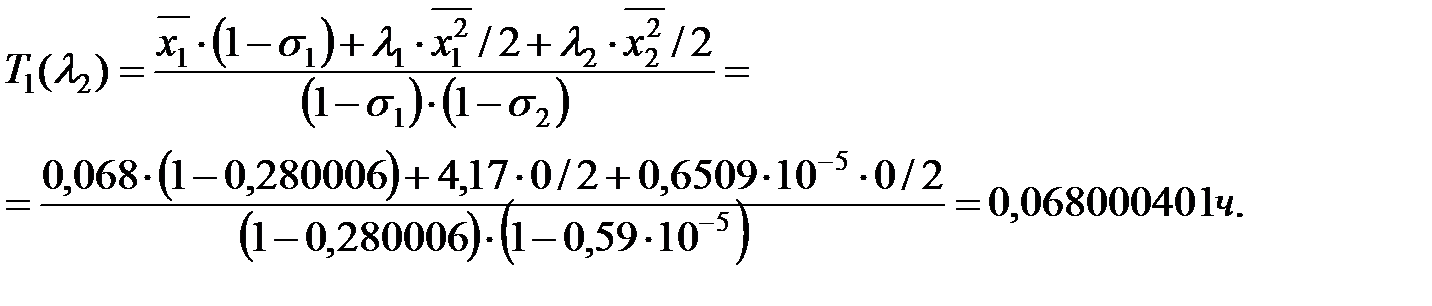
Среднее число простаивающих поездов определяется как:
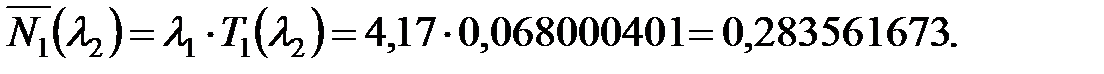
Окончательно, среднее число 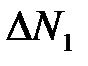 и время дополнительных остановок поездов
и время дополнительных остановок поездов 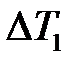 , [ч] вследствие отказов элемента ОИ определяются по формулам:
, [ч] вследствие отказов элемента ОИ определяются по формулам:
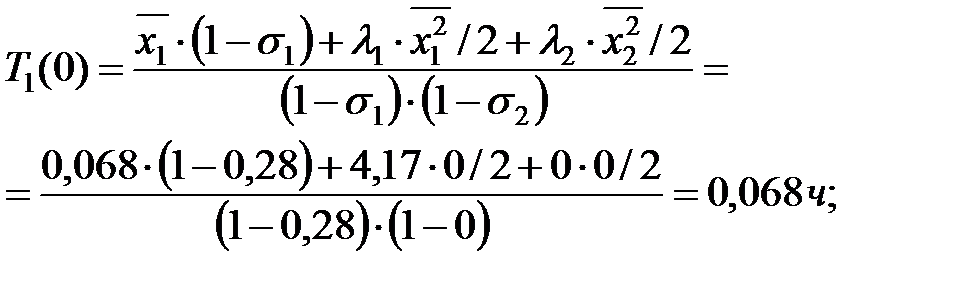
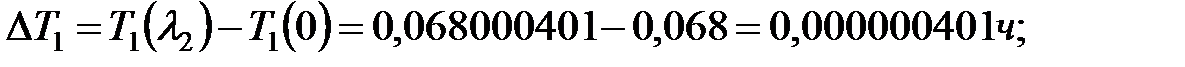
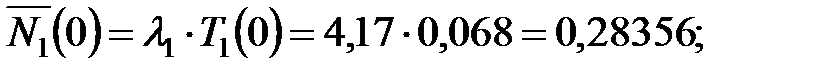
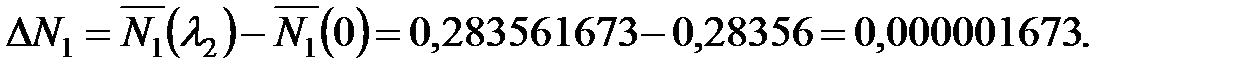
Суммарный ущерб от отказов ОИ вследствие простоя поездов за расчетный период 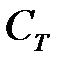 [тыс. руб.] вычисляют по формуле:
[тыс. руб.] вычисляют по формуле:
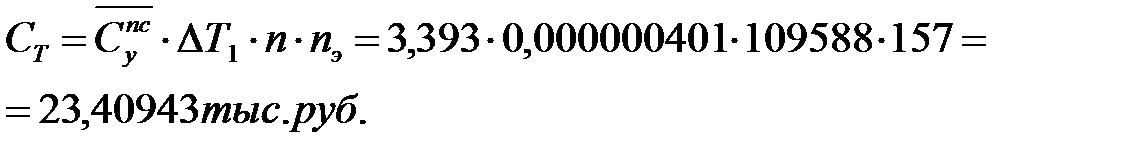
Суммарный ущерб от отказов ОИ вследствие дополнительных остановок поездов за расчетный период 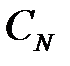 [тыс. руб.] вычисляют по формуле:
[тыс. руб.] вычисляют по формуле:
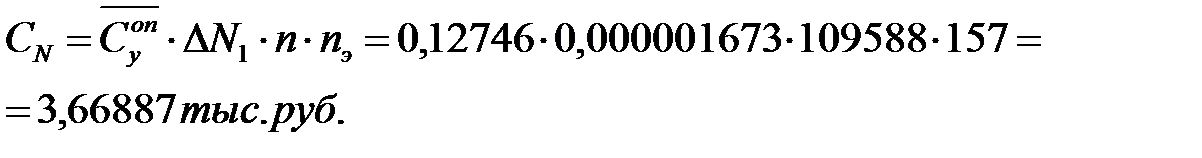
Суммарный ущерб по ОИ составляет:
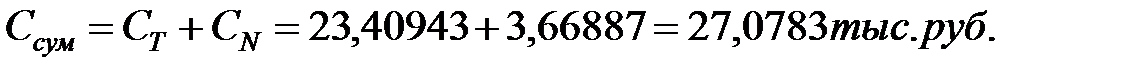
Значения вероятностей состояний ОИ определяется по следующим формулам:
– вероятность использования элемента ОИ:
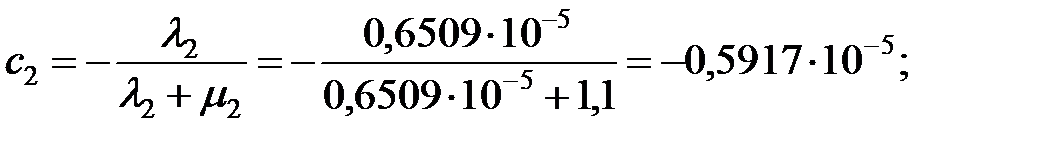
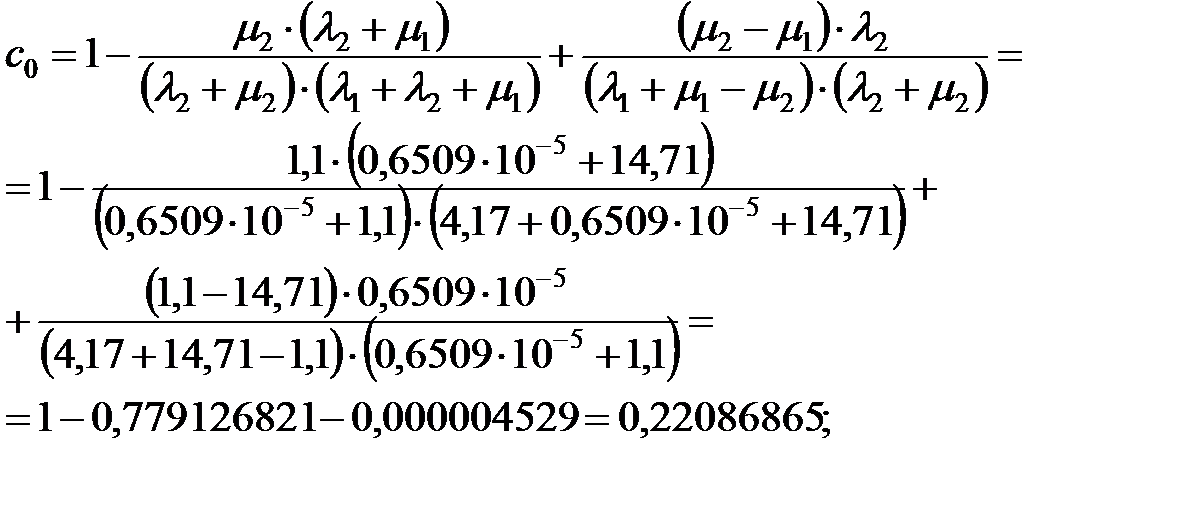
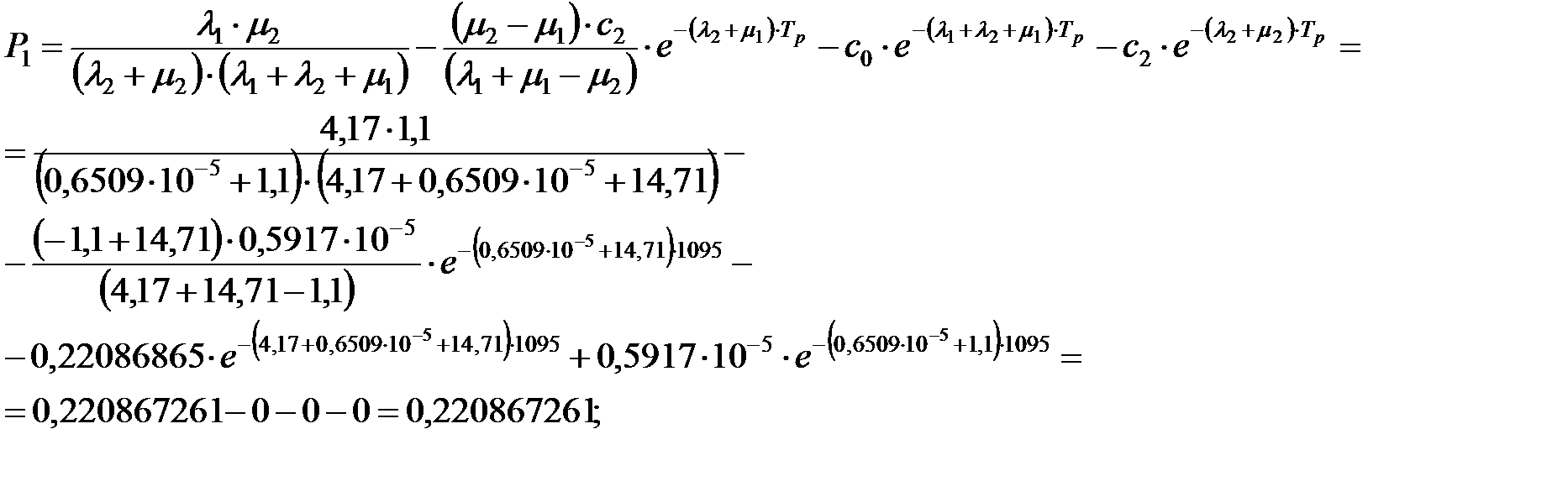
– вероятность отказа элемента ОИ:
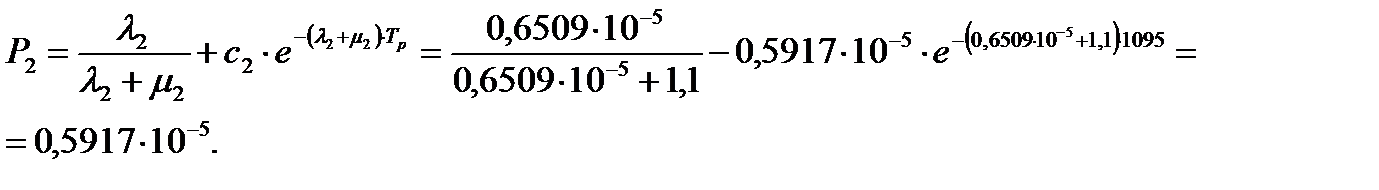
Вероятность риска по безотказности для ОИ:
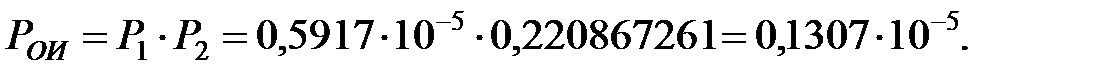
Вывод: определены показатель для оценки вероятности риска по безотказности для ОИ 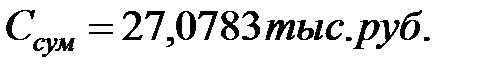 и показатель, характеризующий последствия риска по безотказности для ОИ,
и показатель, характеризующий последствия риска по безотказности для ОИ, 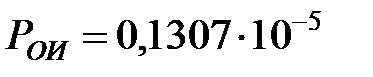 . Полученные показатели используются при анализе риска по безотказности для ОИ на различных этапах жизненного цикла с помощью матриц риска. В таблице 4.17 приведена матрица рисков ОИ. Согласно данной матрице уровень риска функционирования ОИ соответствует уровню К1. Вероятность возникновения ситуации приводящей к риску маловероятна, но возможна. Можно предположить, что данная ситуация может возникнуть в исключительном случае. Возможны незначительные потери. Данный риск считается не принимаемым в расчет (приемлем без согласия ОАО «РЖД»).
. Полученные показатели используются при анализе риска по безотказности для ОИ на различных этапах жизненного цикла с помощью матриц риска. В таблице 4.17 приведена матрица рисков ОИ. Согласно данной матрице уровень риска функционирования ОИ соответствует уровню К1. Вероятность возникновения ситуации приводящей к риску маловероятна, но возможна. Можно предположить, что данная ситуация может возникнуть в исключительном случае. Возможны незначительные потери. Данный риск считается не принимаемым в расчет (приемлем без согласия ОАО «РЖД»).
Таблица 4.17- Матрица риска для ОИ
| Вероятность риска | Уровни тяжести последствий (величина ущерба) | |||||
| < 50 тыс. руб. | 50 – 200 тыс. руб. | 200 – 4000 тыс. руб. | 4000 – 20000 тыс. руб. | > 20000 тыс. руб. | ||
| незначительный | серьезный | критический | катастрофический | бедственный | ||
| 0,9 ≤ PОИ ≤ 1 | Частое | Ч1 | Ч2 | Ч3 | Ч4 | Ч5 |
| 0,1 ≤ PОИ < 0,9 | Вероят-ное | В1 | В2 | В3 | В4 | В5 |
 10-3 ≤ PОИ < 0,1 10-3 ≤ PОИ < 0,1
| Случай-ное | С1 | С2 | С3 | С4 | С5 |
| 10-5 ≤ PОИ < 10-3 | Редкое | Р1 | Р2 | Р3 | Р4 | Р5 |
| 10-7 ≤ PОИ < 10-5 | Крайне редкое | К1 (ОИ) | К2 | К3 | К4 | К5 |
| PОИ < 10-7 | Мало-вероятное | М1 | М2 | М3 | М4 | М5 |
| |
Определение риска по безопасности для ОИ основывается на теории случайных импульсных потоков. Интенсивность отказов ОИ, которые могу привести к нарушению безопасности движения поездов, определяется по формуле:
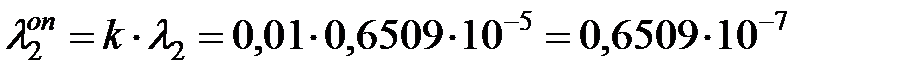 1/ч. 1/ч.
|
Средняя длительность активного состояния ОИ:
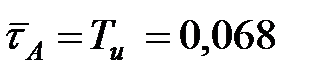 ч. ч.
|
Средняя длительность пассивного состояния ОИ:
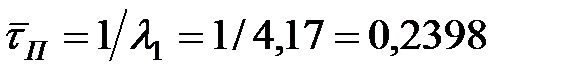 ч. ч.
|
Средняя длительность соответственно опасного и неопасного состояний ОИ:
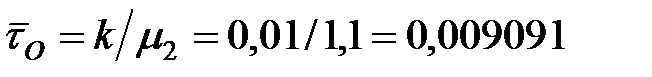 ч. ч.
| |
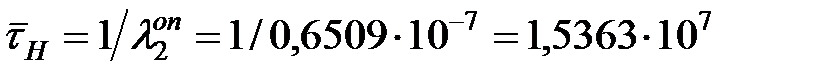 ч. ч.
|
Математическое ожидание длительности совпадения активных и опасных состояний ОИ равно:
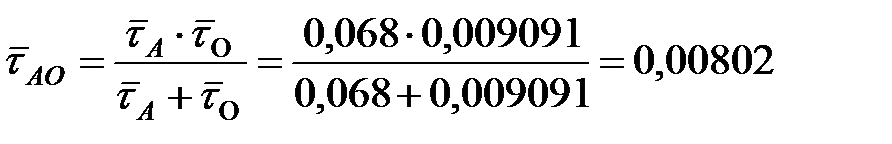 ч. ч.
|
Среднюю интенсивность перехода ОИ в активное опасное состояние можно определить по формуле:
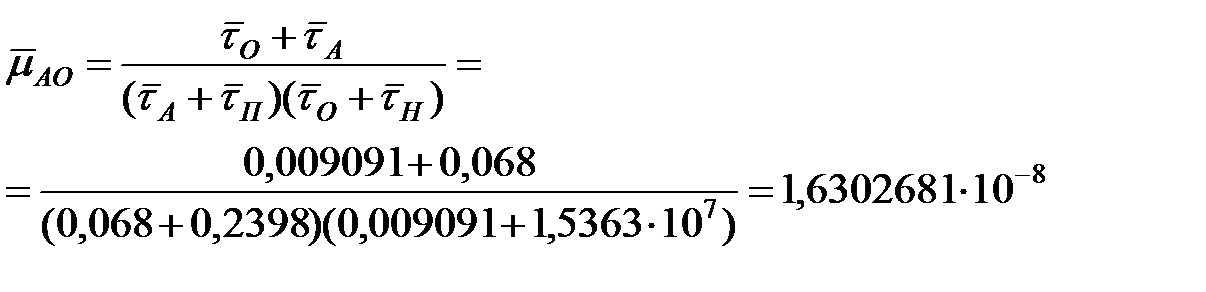 1/ч. 1/ч.
|
Среднюю длительность совокупности следующих состояний ОИ: пассивного опасного, активного неопасного и пассивного неопасного можно определить по формуле:
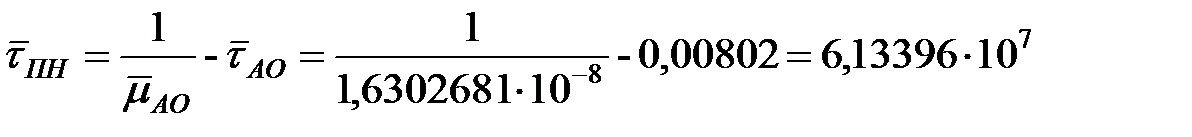 ч. ч.
|
При допущении о том, что случайная величина 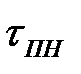 распределена по экспоненциальному закону, параметр закона распределения
распределена по экспоненциальному закону, параметр закона распределения 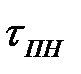 можно определить как:
можно определить как:
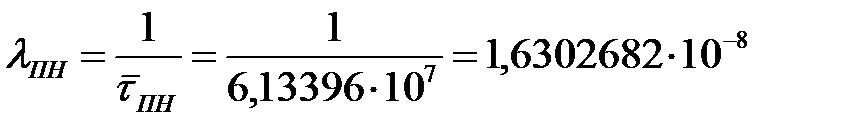 1/ч. 1/ч.
|
За расчетное время 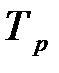 вероятность возникновения риска для ОИ по безопасности при движении поездов определяется по формуле:
вероятность возникновения риска для ОИ по безопасности при движении поездов определяется по формуле:
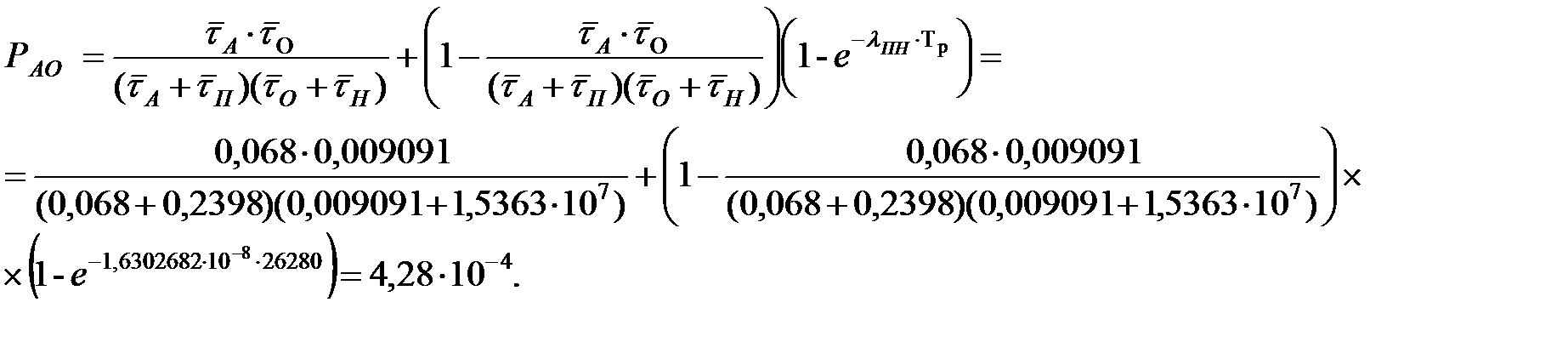
|
В таблице 4.18 приведена матрица рисков по безопасности для ОИ. Согласно данной матрице уровень риска для ОИ соответствует Р3.
Таблица 4.18 – Матрица риска по безопасности для ОИ
| Вероятность риска | Уровни тяжести последствий (величина ущерба) | |||||
| незначительный | серьезный | критический | катастрофический | бедственный | ||
| 0,9 ≤ PОИ ≤ 1 | Частое | Ч1 | Ч2 | Ч3 | Ч4 | Ч5 |
| 0,1 ≤ PОИ < 0,9 | Вероят-ное | В1 | В2 | В3 | В4 | В5 |
| 10-3 ≤ PОИ < 0,1 | Случай-ное | С1 | С2 | С3 | С4 | С5 |
| 10-5 ≤ PОИ < 10-3 | Редкое | Р1 | Р2 | Р3 (ОИ) | Р4 | Р5 |
| 10-7 ≤ PОИ < 10-5 | Крайне редкое | К1 | К2 | К3 | К4 | К5 |
| PОИ < 10-7 | Мало-вероятное | М1 | М2 | М3 | М4 | М5 |
| |
 |
Дата добавления: 2016-03-27; просмотров: 1237;
