Вихревые токи в электропроводящем полупространстве

Если в магнитное поле первичного измерительного преобразователя внести электропроводящий объект, то переменное электромагнитное поле индуцирует в объекте вихревые токи. По закону Ленца направление вихревого тока, а следовательно и магнитного потока, возбужденного им, в каждый момент времени будет направлено так, чтобы противодействовать магнитному потоку, породившему вихревой ток. Как следствие, картина магнитного поля первичного измерительного преобразователя с внесенным в его поле электропроводным объектом исказится. На рис. 2.2 изображена функциональная модель абсолютного трансформаторного двухобмоточного первичного измерительного преобразователя без ферритововых сердечника и экрана с внесенным в его поле электропроводящим объектом в виде полупространства, картина поля и распределение плотности вихревого тока J_вт, наведенного в образце.

На рис. 2.2 изображено направление тока в обмотке возбуждения и направление вихревого тока в электропроводящем объекте контроля. Магнитное поле вихревых токов складывается с магнитным полем обмотки возбуждения по принципу суперпозиции.

Рис. 2.2. Функциональная модель абсолютного трансформаторного двухобмоточного первичного измерительного преобразователя без ферритовых сердечника и экрана с внесенным в его поле электропроводящим объектом в виде полупространства

Для расчета параметров взаимодействия первичного измерительного преобразователя с электропроводящим объектом контроля удобно отказаться от абсолютных величин и перейти к относительным, нормированным по радиусу обмотки возбуждения R_в. В этом случае относительный радиус обмотки возбуждения R_в^*= R_в/ R_в = 1.

Распределение плотности J_вт и значение фазы j_вт вихревого тока в различных точках объема электропроводящего объекта под обмоткой возбуждения отлично. Наибольшая плотность вихревого тока наблюдается в случае, если зазор между обмоткой возбуждения и поверхностью контролируемого объекта h^* = 0 (непосредственно возле поверхности объекта под эквивалентным витком обмотки возбуждения R_Jmax^* = 1). В случае если существует зазор между обмоткой возбуждения и поверхностью объекта контроля h^* > 0, то наибольшая плотность вихревых токов наблюдается на большем расстоянии от центра обмотки возбуждения (R_Jmax^* > 1). Это обусловливается изменением формы магнитного поля обмотки возбуждения с увеличением зазора. Для ориентировочной оценки этой величины можно воспользоваться эмпирической формулой:

R_Jmax = R_в + 1,5h^* (2.1.7)

С увеличением глубины плотность вихревого тока уменьшается по закону, близкому к экспоненциальному.

Значение фазы j_вт вихревого тока в точке наибольшей плотности тока, непосредственно под поверхностью объекта контроля, сдвинуто на более чем на 180⁰ относительно тока в обмотке возбуждения. При удалении от поверхности вглубь, j_вт увеличивается.

Глубина проникновения вихревых токов определяется радиусом обмотки возбуждения, частотой тока возбуждения, электропроводностью и магнитной проницаемостью материала контролируемого объекта. Для расчета глубины проникновения вихревого тока и ЭДС, наводимой на измерительной обмотке, удобно использовать обобщенный параметр b, который учитывает влияние всех перечисленные выше параметров:

_______

b = RÖ(wsm₀m_r), (2.1.8)

где R – эквивалентный радиус обмотки возбуждения, [м], (при

h* = 0, R = R_в); w - круговая частота тока возбуждения, [рад/сек];

s – электропроводность основания, [См/м]; m₀ – магнитная постоянная; m_r – относительная магнитная проницаемость основания.

На рис. 2.3 представлены графики распределения относительного значения плотности вихревого тока J_вт^* = J_вт/(I_в R^* W_в^*) в зависимости от расстояния от оси преобразователя R* =R/R_в и глубины z* = z/ R_в.

а) 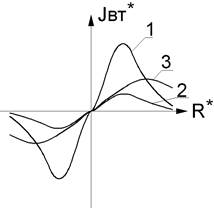б)

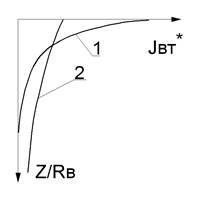
Рис.2.3. Зависимость относительного значения плотности вихревых

токов:

а - по поверхности: 1 – b = 5 (h* = 0); 2 – b = 1,5 (h* = 0); 3 – b = 5

(h* = 0,7), б - по глубине: 1 – b = 5 (h* = 0); 2 – b = 1,5 (h* = 0).

На рис. 2.4 изображены графики значения фазы вихревого тока по глубине z* и по расстоянию от оси преобразователя R*.

а) 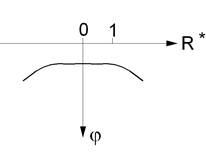б)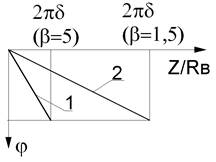

Рис.2.4. Зависимость значения фазы вихревого тока:

а - по поверхности; б - по глубине:

1 – b = 5 (h* = 0); 2 – b = 1,5 (h* = 0).

Для оценки относительной глубины проникновения вихревых токов d* = d/R_в можно использовать формулу определения глубины проникновения плоской волны с учетом поправочного коэффициента

k_ф = 0,4+0,13 ln (b) k_ф

_

d* =k_ф(Ö2 )/ b (2.1.9)

Разность фаз вихревого тока протекающего на глубине равной длине электромагнитной волны в металле l₁=2pd и тока протекающего по поверхности составляет 2p. Глубину проникновения вихревых токов, равную 2pd считают максимальной глубиной проникновения вихревого тока.