Фазовый метод измерения толщины неферромагнитных электропроводящих покрытий на неферромагнитном электропроводящем основании

Как упоминалось ранее, измерение толщины электропроводящего покрытия – это измерение значения интегральной электропроводности в объеме металла, в котором распространяются вихревые токи. На рис. 2.58, а) изображен годограф вектора разностного напряжения ∆Ů при изменении обобщенного параметра b (электропроводности полупространства). Выбор оптимальных параметров преобразователя, в первую очередь, диаметра и частоты возбуждения, должен производиться с использованием этим данных. На рис. 2.58, б) изображен график зависимости проекции приращения вектора разностного напряжения ∆Ů при изменении электропроводности полупространства на нормаль к направлению влияния зазора от начального значения обобщенного параметра b.

а) 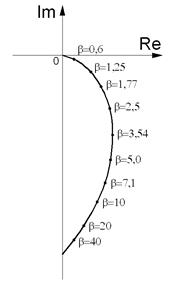б)

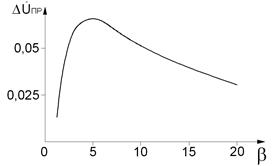
Рис. 2.58. График зависимости разностного напряжения от обобщенного параметра b: а - годограф вектора разностного напряжения ∆Ů при изменении обобщенного параметра b (электропроводности полупространства, при h*=0,5), б - график зависимости проекции приращения вектора разностного напряжения ∆Ů при изменении электропроводности полупространства на нормаль к направлению влияния зазора от начального значения обобщенного параметра b

Из рис. 2.58, б видно, что при начальном значении b = 5, увеличение или уменьшение его приводит к наибольшему изменению фазы вектора разностного напряжения ∆Ů в случае измерения толщины с отстройкой от влияния зазора. Для расчета значения b следует использовать значение электропроводности основания, а не покрытия.

Таким образом, при решении задачи измерения толщины этой группы покрытие/основание, исходя из электропроводности основания, можно рассчитать оптимальное соотношение частоты преобразователя и его диаметра. Это соотношение определяется по формуле:

__ ___

RÖw = (Ös₀ m₀)/ 5 , (2.12.1)

где R – эквивалентный радиус преобразователя.

Частота возбуждения и радиус преобразователя выбираются исходя из максимальной толщины покрытия и технологических ограничений на диаметр и частоту возбуждения.

Изменение толщины электропроводящего покрытия приводит к изменению фазы вектора разностного напряжения ∆Ů по нелинейному закону, и в некоторых случаях даже не по монотонному. Это связано с тем, что вихревой ток различной плотности в покрытии и в основании влияют друг на друга, искажая общую картину вторичного магнитного поля. Поэтому говорить о неком интегральном значении электропроводности можно только условно. Для уточнения влияния изменения толщины покрытия на показания толщиномера, на рис. 2.59 изображены годографы изменения вектора разностного напряжения ∆Ů при изменении толщины покрытия различной электропроводности. Параметры преобразователя выбраны оптимальными, при которых b(s_осн) = 5 (точка А).

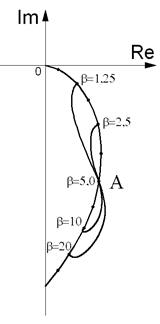
Рис. 2.59. Годографы изменения вектора разностного напряжения ∆Ů при изменении толщины покрытия различной электропроводности.

В случае, если s_П < s_осн конец вектора ∆Ů будет располагаться выше точки А, если s_П > s_осн конец вектора ∆Ů будет располагаться ниже точки А.

График зависимости максимального изменения фазы вектора напряжения ∆Ů при изменении толщины покрытия от 0 до 2pd от отношениях электропроводностей покрытия и основания s_П / s_осн приведен на рис. 2.60.

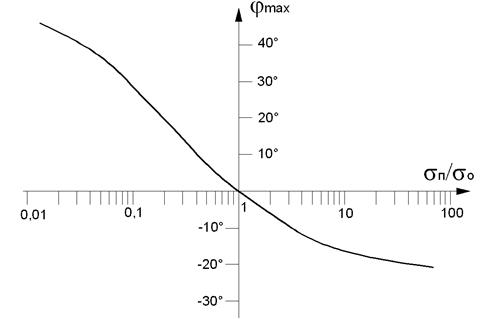
Рис. 2.60. Зависимость максимального изменения фазы вектора ∆Ů при изменении толщины покрытия от 0 до 2pd от отношения s_П / s_осн.

График зависимости фазы вектора напряжения ∆Ů от относительной толщины покрытия Т_П/R приведен на рис. 2.61.

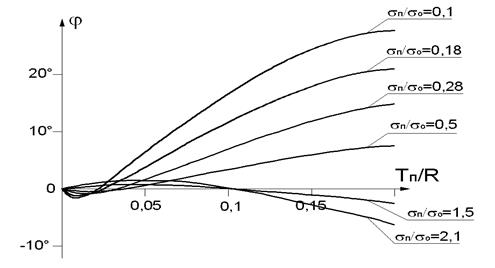
Рис.2.61. График зависимости фазы вектора напряжения ∆Ů от относительной толщины покрытия Т_П/R.

Из рис. 2.61 видно, что в определенном диапазоне малых толщин покрытий возникает неоднозначность. Фаза вектора напряжения ∆Ů вначале имеет один знак, затем пересекает ось начального значения, а затем изменяется в противоположную сторону вплоть до насыщения. Этот небольшой участок неопределенности называется «мертвой зоной» вихретокового фазового толщиномера. Поэтому вихретоковые фазовые толщиномеры не могут измерять толщину покрытий данной группы от нуля, всегда существует некоторое значение минимальной измеряемой толщины покрытия. Изменяя балансировку и параметры преобразователя можно уменьшить величину «мертвой зоны», однако полностью от неё избавиться невозможно.

Рассмотрим пример измерения толщины серебряного покрытия на латунном основании.

Электропроводность латуни Л63 s_осн = 9,3 МСм/м, электропроводность серебра s_П = 60 МСм/м. Отношение s_П / s_осн » 6,5. Исходя из графика на рис. 2.61 максимальное изменение фазы вектора ∆Ů » 15°. Конструктивный заданный радиус преобразователя R =1,3 мм. Расчетное значение оптимальной частоты f » 200 кГц.

На рис. 2.62, а изображен годограф изменения вектора ∆Ů при изменении толщины, на рис. 2.62, б изображен график зависимости изменения фазы вектора ∆Ů от толщины покрытия (градуировочная характеристика).

а) 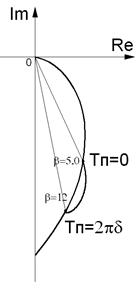б)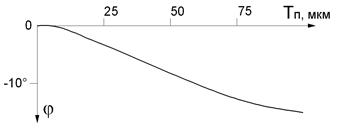

Рис. 2.62. Изменение вектора напряжения ∆Ů при изменении толщины серебряного покрытия на латунном основании:

а – годограф, б - график изменения фазы (градуировочная характеристика)

Из (2.1.9) следует, что максимальная глубина проникновения вихревого тока d » 200 мкм.

Иногда в качестве подслоя под серебро используют слой медного покрытия. Учитывая, что электропроводность чистой меди практически не отличается от электропроводности серебра, при измерении толщины такого двухслойного покрытия результатом будет суммарная толщина медного и серебряного покрытий.

Измерение толщины неферромагнитных электропроводящих покрытий на неферромагнитном электропроводящем основании с применением фазового метода возможно при достаточном отличии электропроводностей покрытия и основания, в противном случае фазовые сдвиги не позволят получить приемлемой погрешности измерений.

Измерение толщины неферромагнитных электропроводящих покрытий на диэлектрическом основании (измерение толщины листовых неферромагнитных электропроводящих материалов)

Задачи этой группы весьма распространены. В первую очередь это измерение толщины химически осажденной меди на пластиковых изделиях для дальнейшего покрытия их никелем или хромом (например, декоративные элементы сантехники и т.п.). Так же к этой группе следует отнести задачи измерения толщины листовых материалов, например алюминиевой или медной фольги, листов, полос при изготовлении или входном (выходном) контроле.

Оптимальным, для решения задач этой группы, является фазовый метод толщинометрии. На рис. 2.63 изображены годографы изменения вектора разностного напряжения ∆Ů при изменении толщины листового электропроводящего металла.

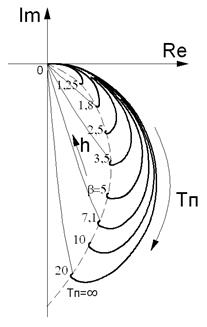
Рис. 2.63. Годографы изменения вектора разностного напряжения ∆Ů при изменении толщины листового электропроводящего металла.

На рис. 2.63 тонкой пунктирной линией изображен годограф при изменении обобщенного параметра b (Т_П=¥), тонкими сплошными – годографы при изменении величины зазора между листовым электропроводящим неферромагниным материалом и преобразователем.

Для выбора оптимальной частоты преобразователя следует учитывать ряд особенностей задачи. Наибольшая чувствительность по фазе наблюдается при значении параметра b = 5 (Т_П=¥), однако эта область характеризуется «насыщением» преобразователя и отсутствием чувствительности к изменению толщины покрытия. К тому же в этой области характеристики наблюдается «мертвая зона», в которой одной той же фазе сигнала соответствуют два значения толщины листового материала. По этому частоту преобразователя следует выбирать незначительно выше. Оптимальными параметрами можно считать те, при которых значение обобщенного параметра b = 7…20 (Т_П=¥). Минимальная толщина контролируемого материала определяется радиусом преобразователя R и составляет, ориентировочно,

Т_Пmin » 0,005·R (2.12.2)

Максимальная толщина контролируемого материала определяется глубиной проникновения вихревого тока (с учетом поправочного коэффициента, формула (2.9)) и составляет не более 2d*. Максимальная измеряемая толщина контролируемого материала будет определяться по формуле:

_

Т_пmax= ((0,4+0,13ln(b))R2Ö2)/ b (2.12.3)

Рассмотрим, в качестве примера, измерения толщины медного покрытия на диэлектрическом (пластиковом) основании.

Электропроводность медного покрытия s_П = 60 МСм/м. Конструктивный заданный радиус преобразователя 1,3 мм. Оптимальная частота возбуждения f » 500 кГц. Диапазон измеряемых толщин составляет от 7 до 145 мкм.

На рис. 2.64, а изображен годограф изменения вектора напряжения ∆Ů при варьировании толщины покрытия, на рис. 2.64, б изображен график зависимости изменения фазы напряжения ∆Ů от толщины покрытия (градуировочная характеристика).

а) 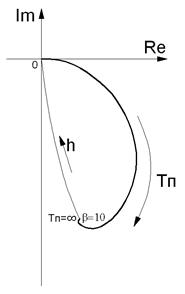б)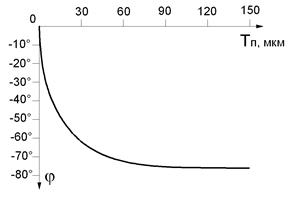

Рис. 2.64. Изменение вектора разностного напряжения ∆Ů при изменении толщины медного покрытия на диэлектрическом основании:

а – годограф, б - график изменения фазы (градуировочная характеристика)

Рассмотрим, в качестве примера, задачу измерения толщины листов, изготовленных из алюминиевого сплава Д16.

Электропроводность листов из сплава Д16 s_Л = 17 МСм/м. Толщина контролируемых листов от 0,75 мм до 1,25 мм. Исходя из этих данных, максимальный допустимый радиус преобразователя может составлять 150 мм, минимальный допустимый радиус - 6,5 мм. Из предложенного достаточно широкого диапазона выберем радиус обмотки 10 мм. Оптимальная частота возбуждения f » 5 кГц (b = 8,2). Диапазон измеряемых толщин, определенный по формулам (2.15 ) и (2.16) от 0,035 мм до 2,5 мм.

Часто в практических задачах возникают особые требования, например, по допустимому максимальному размеру преобразователей или по минимальному допустимому радиусу кривизны поверхности контролируемого объекта. В первом случае ограничение по размерам преобразователя приходится принимать искусственно, вопреки расчетам, во втором случае можно опираться на практический опыт. Если радиус кривизны поверхности контролируемого объекта больше чем 2 диаметра преобразователя – вносимой погрешностью можно пренебречь; если меньше 2 диаметров, но больше 1 диаметра преобразователя – возникает незначительное искажение характеристики преобразователя, для устранения которой следует производить калибровку толщиномера; если меньше 1 диаметра – характеристика преобразователя искажается существенно.

В любом случае толщиномер может производить измерения при неоптимальных радиусе преобразователя и частоте возбуждения, однако его характеристики ухудшаются.

Так, если в представленном примере есть ограничение по максимальному радиусу преобразователя, например 3,5 мм, то при той же частоте возбуждения f = 5 кГц значение параметра b = 2,9 и диапазон измеряемых толщин составит от 0,018 мм до 1,9 мм.

Для сравнения на рис. 2.65, а изображены годографы изменения вектора разностного напряжения ∆Ů при изменении толщины покрытия, на рис. 2.65, б изображены графики зависимости изменения фазы разностного напряжения ∆Ů от толщины покрытия (градуировочная характеристика) в первом и втором случае.

а) 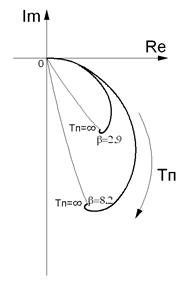б)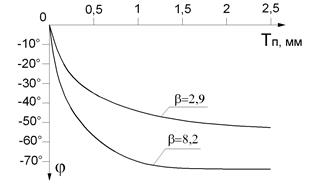

Рис. 2.65. Изменение вектора напряжения ∆Ů при изменении толщины медного покрытия на диэлектрическом основании: а – годограф,

б - график изменения фазы (градуировочная характеристика)

Приведенные примеры показывают широкий спектр возможного применения вихретокового фазового метода.

Приведенные алгоритмы и схемы реализованы в вихретоковых преобразователях для электромагнитных толщиномеров «Константа К5» и «Константа К6». На рис. 2.66 изображена структурная схема данных толщиномеров.

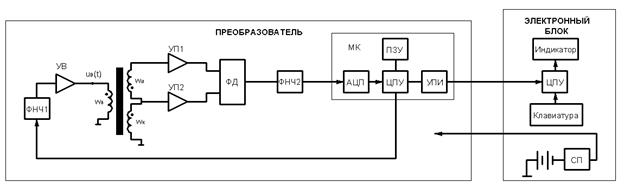
Рис. 2.66. Структурная схема электрормагнитных толщиномеров «Константа К5» и «Константа К6» с вихретоковым фазовым преобразователем: ФНЧ – фильтр низких частот, ФД – фазовый детектор, АЦП – аналого – цифровой преобразователь, ЦПУ – центральное процессорное устройство, УПИ – универсальный приемо-передающий интефейс, ПЗУ – постоянное запоминающее устройство, УВ, УП – усилители, МК – микроконтроллер, СП – стабилизатор напряжения питания

Вся аналоговая электронная схема обработки сигналов вместе с микроконтроллером, содержащим АЦП, расположена на плате внутри корпуса преобразователя. За счет этого существенно улучшены метрологические характеристики толщиномера и существенно расширен частотный диапазон (до 4 МГц). Микроконтроллер внутри преобразователя содержит блок УПИ (универсальный последовательный интерфейс) с помощью которого происходит обмен данными между преобразователем и электронным блоком. В ПЗУ микроконтроллера преобразователя хранятся градуировочные характеристики и прочие необходимые данные. Это позволяет не привязывать преобразователь к конкретному электронному блоку. Например, используя эту технологию, можно градуировать преобразователи отдельно, записывать в память преобразователя его градуировочные характеристики и передавать заказчику.