ТЕМА 7. ОБРАБОТКА РЕЗУЛЬТАТОВ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ

7.1 Применение вероятностных методов при обработке результатов измерений

Из теории вероятности известно, что наиболее универсальным способом описания случайных величин является отыскание их интегральных или дифференциальных функций распределения.

Интегральной функцией распределения F(x)(рисунок 7.1, а) называют функцию, каждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина x_i в i-ом опыте принимает значение, меньшее х:

F(x) = P{x_i < x} = P{- ∞ < x_i ≤ x}. (7.1)

Свойства F(x):

1) неотрицательная, т.е. F(x) ≥ 0;

2) неубывающая, т.е. F(x₂) ≥ F(x₁), если x₂ ≥ x₁;

3) область определений – от 0 до 1, т.е. F(- ∞) = 0; F(+ ∞) = 1;

4) вероятность нахождения случайной величины х в диапазоне от х₁ до х₂ P{x₁ < x_i < x} = F(x₂) – F(x₁).

Более наглядным является описание свойств результатов измерений и случайных погрешностей с помощью дифференциальной функции распределения (рисунок 7.1, б), иначе называемой плотностью распределения вероятностей p(x)=dF(x)/dx. Она всегда неотрицательна и подчиняется условию нормирования в виде:

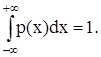(7.2)

Учитывая взаимосвязь F(х) и р(х), легко показать, что вероятность попадания случайной величины в заданный интервал (х₁; х₂) 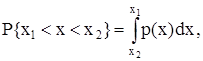следовательно, рассмотренное выше условие нормирования (7.2) означает, что вероятность попадания в интервал (- ∞; + ∞) равна единице, т.е. представляет собой достоверное событие. Кроме того, из этого выражения следует, что вероятность попадания случайной величины х в заданный интервал (х₁; х₂) равна площади, заключенной под кривой р(х) между абсциссами х₁ и х₂ (рисунок 7.1, б). Поэтому по форме кривой плотности распределения вероятности р(х) можно судить о том, какие значения случайной величины х наиболее вероятны, а какие – наименее.

7.2 Обработка результатов многократных измерений

При однократных измерениях оценку погрешности производят на основе класса точности используемых средств измерений.

Получаемый при этом предел допускаемой погрешности СИ неполно характеризует качество измерений, т.е. остается неизвестным закон распределения вероятностей погрешностей и не ясно, какая из составляющих систематическая Δ_сист или случайная Δ_случ доминируют в сумме:

Δ = Δ_сист + Δ_случ . (7.3)

Для того чтобы оценить случайную погрешность и определить более точно усредненный результат измерения проводят многократные наблюдения и дальнейшую статистическую обработку получаемых результатов.

Структура погрешности в каждой точке шкалы СИ полностью характеризуется плотностью распределения вероятностей.

Существует множество законов распределения случайных величин: нормальный (распределение Гаусса), экспоненциальный, равномерный арксинусный и т.д. В зависимости от того, по какому закону распределены результаты измерений, происходит их статистическая обработка. Для определение оценки плотности распределения вероятностей требует проведения нескольких сотен измерений.

При некоторых ограничениях распределение большинства независимых случайных величин можно свести к распределению Гаусса. Поэтому на практике чаще всего имеют дело с нормальным распределением.

Результаты наблюдений, являющихся случайными величинами х_i, распределены по нормальному закону (закону Гаусса), если их плотность вероятностей имеет вид:

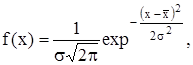(7.4)

где σ – среднеквадратическое отклонение;

х – математическое ожидание.

Для решения многих задач не требуется знания функции и плотности распределения вероятностей, а вполне достаточными характеристиками случайных погрешностей служат их простейшие числовые характеристики: математическое ожидание и среднеквадратическое отклонение. Числовые вероятностные характеристики погрешностей, представляющие собой неслучайные величины, теоретически определяются при конечном числе опытов. Практически число опытов всегда ограничено, поэтому реально пользуются числовыми характеристиками, которые принимают за искомые вероятностные характеристики и называют оценками характеристик. Определение оценок числовых характеристик может быть выполнено по значительно меньшему числу наблюдений – порядка 10-20.

Пусть при измерении величины А N раз получен ряд значений х₁, х₂, х₃ ... х_N. Если число измерений N достаточно велико, то за истинное значение измеряемой величины принимают наиболее достоверное значение – среднее арифметическое (действительное):

(7.5)

Зная среднее арифметическое значение, можно определить отклонение результата единичного измерения от среднего значения:

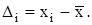(7.6)

Это отклонение может быть вычислено для каждого измерения. Следует помнить, что сумма отклонения результата измерений от среднего значения равна нулю, а сумма их квадратов минимальна. Эти свойства используются при обработке результатов измерений для контроля правильности вычислений.

Среднее квадратическое отклонение (СКО) погрешности однократного измерения равно:

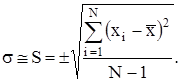(7.7)

В теории случайных погрешностей вводится также понятие о среднем квадратическом отклонении среднего арифметического 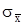(средняя квадратическая погрешность результата измерений):

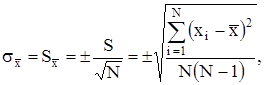(7.8)

где 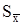– оценка средней квадратической погрешности 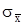ряда из N измерений.

При оценке результатов измерений пользуются понятием предельно допустимой (максимальной) погрешности ряда измерений:

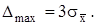(7.9)

Рассмотренные оценки результатов измерений, выражаемые одним числом, называют точечными оценками. Поскольку подобную оценку обычно принимают за действительное значение измеряемой величины, то возникает вопрос о точности и надежности полученной оценки. Судят об этом по вероятности α того, что результат измерений (действительное значение) отличается от истинного не более чем на Δ. Это можно записать в виде:

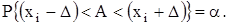(7.10)

Вероятность α называется доверительной вероятностью или коэффициентом надежности, а интервал значений от (х – Δ) до (х + Δ) – доверительным интервалом. Обычно его выражают в долях средней квадратической погрешности:

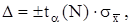(7.11)

где t_α(N) – табулированный коэффициент распределения Стъюдента, который зависит от доверительной вероятности α и числа измерений N.

Результат измерения записывается в виде:

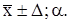(7.12)