Несимметричный режим трехфазной цепи

Один из наиболее часто встречающихся случаев несимметричного режима трехфазной цепи получается при соединении фаз несимметричного приемника звездой без нейтрального провода или с нейтральным проводом, комплексное сопротивление которого 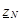необходимо учитывать при расчете (рис. 4,а).

Приведенная на рисунке 4,а схема имеет две нейтральные точки: симметричного генератора N и несимметричного приемника n – два узла цепи. Для расчета режима работы воспользуемся формулой межузлового напряжения. В рассчитываемой трехфазной системе комплексное значение напряжения 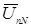между нейтральными точками приемника и генератора называется напряжением смещения нейтрали. Это напряжение

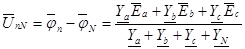. (11)

С учетом равенств

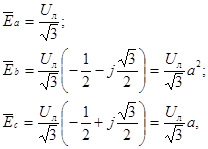(12)

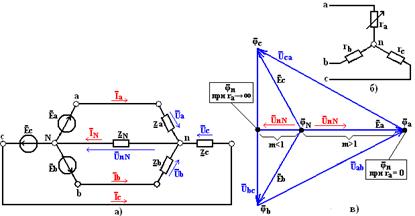
Рисунок 4

где 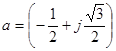- фазный коэффициент,-

перепишем (11) в виде

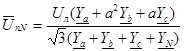. (13)

Фазные напряжения приемника определяются по второму закону Кирхгофа:

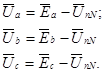(14)

По закону Ома фазные токи и ток в нейтральном проводе соответственно равны

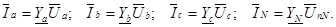(15)

Распределение напряжений между фазами несимметричного приемника, фазы которого соединены звездой, показано на потенциальной диаграмме (рис. 4,в).

При построении потенциальной диаграммы равный нулю потенциал выбран у нейтральной точки N генератора, которая служит началом отсчета. Из начала отсчета построены три вектора фазных ЭДС генератора 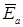, , 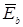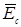. Концы этих векторов определяют комплексные значения потенциалов 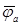, , 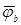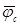линейных проводов при 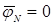, а, следовательно, и линейных напряжений 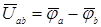, , 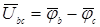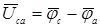. При симметричном приемнике нет смещения нейтрали, т.е 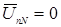и потенциал нейтральной точки приемника 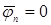. Поэтому на диаграмме потенциал нейтральной точки приемника 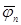совпадает с нейтральной точкой генератора 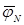. При несимметричном приемнике смещение нейтрали 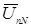не равно нулю. Поэтому потенциал нейтральной точки приемника 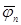смещается относительно потенциала нейтральной точки генератора 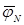, т.е. из центра треугольника линейных напряжений.

Рассмотрим простейший случай приемника с активными сопротивлениями фаз r_a и r_b = r_c = r при отсутствии нейтрального провода (рис. 4,б). Проводимости фаз b и c одинаковые: g_b = g_c = g = 1/r, а проводимость g_a = 1/r_a фазы а изменяется от 0 до ∞. Приняв g_a/g = m, определим смещение нейтрали:

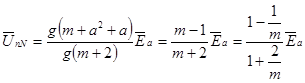. (16)

При изменениях проводимости g_a в пределах от нуля до бесконечности множитель при ЭДС 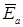остается действительной величиной. Следовательно, напряжение смещения нейтрали 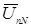совпадает по фазе с ЭДС 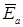при m > 1, а при m < 1 их фазы отличаются на π (рис. 4,в). В частности, при размыкании фазы а, т.е. g_a = 0 или r_a → ∞ и m = 0, смещение нейтрали

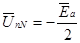. (17)

При этом фазные напряжения приемника

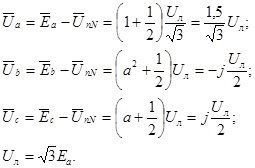(18)

При g_a → ∞ или r_a = 0, т.е. при коротком замыкании точек а и n, , , .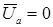

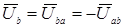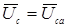Потенциал нейтральной точки приемника может сместиться далеко за пределы треугольника линейных напряжений, если проводимости фаз приемника, соединенных звездой без нейтрального провода, различны по характеру.