Основные параметры и построение помехоустойчивых кодов

Проблема повышения верности обусловлена не соответствием между требованиями, предъявляемыми при передаче данных и качеством реальных каналов связи. В сетях передачи данных требуется обеспечить верность не хуже 10-6 - 10-9, а при использовании реальных каналов связи и простого (первичного) кода указанная верность не превышает 10-2 - 10-5.

Одним из путей решения задачи повышения верности в настоящее время является использование специальных процедур, основанных на применении помехоустойчивых (корректирующих) кодов.

Простые коды характеризуются тем, что для передачи информации используются все кодовые слова (комбинации), количество которых равно N=qn (q - основание кода, а n - длина кода). В общем случае они могут отличаться друг от друга одним символом (элементом). Поэтому даже один ошибочно принятый символ приводит к замене одного кодового слова другим и, следовательно, к неправильному приему сообщения в целом.

Помехоустойчивыми называются коды, позволяющие обнаруживать и (или) исправлять ошибки в кодовых словах, которые возникают при передаче по каналам связи. Эти коды строятся таким образом, что для передачи сообщения используется лишь часть кодовых слов, которые отличаются друг от друга более чем в одном символе. Эти кодовые слова называются разрешенными. Все остальные кодовые слова не используются и относятся к числу запрещенных.

Применение помехоустойчивых кодов для повышения верности передачи данных связанно с решением задач кодирования и декодирования.

Задача кодирования заключается в получении при передаче для каждой k - элементной комбинации из множества qk соответствующего ей кодового слова длиною n из множества qn.

Задача декодирования состоит в получении k - элементной комбинации из принятого n - разрядного кодового слова при одновременном обнаружении или исправлении ошибок. [6]

Основные параметры помехоустойчивых кодов

Длина кода - n;

Длина информационной последовательности - k;

Длина проверочной последовательности - r=n-k;

Кодовое расстояние кода - d0;

Скорость кода - R=k/n;

Избыточность кода - Rв;

Вероятность обнаружения ошибки (искажения) - РОО;

Вероятность не обнаружения ошибки (искажения) - РНО.

Кодовое расстояние между двумя кодовыми словами (расстояние Хэмминга) - это число позиций, в которых они отличаются друг от друга.

Кодовое расстояние кода - это наименьшее расстояние Хэмминга между различными парами кодовых слов.

Стиранием называется "потеря" значения передаваемого символа в некоторой позиции кодового слова, которая известна.

Код, в котором каждое кодовое слово начинается с информационных символов и заканчивается проверочными символами, называется систематическим.

Построение помехоустойчивых кодов в основном связано с добавлением к исходной комбинации (k-символов) контрольных (r-символов) Закодированная комбинация будет составлять n-символов. Эти коды часто называют (n,k) - коды.

k—число символов в исходной комбинации

r—число контрольных символов

Рассмотрим основные понятия помехоустойчивого кодирования. Двоичный (n,k)-код предполагает правило перехода от комбинации из k информационных символов, общее число которых 2k, к такому же числу кодовых комбинаций длиной n (причем n > k), общее число которых 2n , т.е. к введению избыточности (для систематических кодов избыточных символов). Для кода существует множество из 2k разрешенных кодовых комбинаций длиной n, каждая из которых соответствует одной из информационных комбинаций. Если сравнить пару кодовых комбинаций длиной n символов, то число двоичных символов в которых они не совпадают, называют расстоянием. Если попарно сравнить все кодовые комбинации, минимальное из полученных расстояний называют кодовым расстоянием d, которое описывает способность кода исправлять или обнаруживать искажения в канале кодовых комбинаций.

Декодирование кода может производиться либо в режиме обнаружения ошибки, либо в режиме исправления ошибок. Если полученная из канала кодовая комбинация является одной из разрешенных, то она считается принятой правильно, хотя на самом деле могла передаваться другая разрешенная комбинация. Если принятая комбинация не является одной из разрешенных комбинаций, то в режиме обнаружения ошибки фиксируется факт обнаружения ошибки, и кодовая комбинация, в общем случае, стирается, т.е. удаляется из дальнейшей обработки, а в режиме исправления ошибки предпринимается попытка исправить искажение (исправить ошибки).

Исправление ошибки выполняется по какому-то правилу или критерию выбора разрешенной комбинации, в которую преобразуется принятая искаженная комбинация (не равная передаваемой в канал связи). При декодировании двоичных алгебраических кодов используется принцип максимума правдоподобия, в основу которого положено предположение, что в канале связи вероятность ошибки большей кратности меньше вероятности меньшей кратности. Т. е. если в канале может исказиться один из символов кодовой комбинации (кратность ошибки t = 1 ), два символа ( t = 2), три символа (t = 3) и т.д., то справедливо для вероятностей искажения Р(t = 1) > Р(t = 2) > Р(t = 3) … Если такое предположение справедливо для используемого дискретного канала, то в декодере, который не знает, что было искажено в принятой кодовой комбинации, оправдано отождествить с передаваемой комбинацией ту из разрешенных комбинаций, которая ближе по расстоянию от комбинации, подлежащей исправлению. Самая близкая (отличающаяся в меньшем числе символов) разрешенная комбинация считается переданной и объявляется результатом исправления ошибки.

При декодировании по принципу максимума правдоподобия справедливо утверждение, что код с кодовым расстоянием d правильно исправляет число ошибок t =[(d-1)/2], где [a] – меньшее целое от а. В то же время ясно, что если реальное число искаженных символов в кодовом блоке превышает величину [(d-1)/2], то произойдет неверное исправление ошибки (ошибка декодирования с вероятностью Рош ). Таким образом, код правильно исправляет ошибки с кратностью не выше [(d-1)/2], при этом число искаженных символов в принимаемой информационной последовательности уменьшается, и вносит ошибки декодирования в результате исправления ошибок с кратностью, превышающей величину [(d-1)/2], когда число искажений в информационной последовательности увеличивается (остаются искажения, полученные в канале связи, и добавляется неверное исправление в декодере). Понятно, что если в канале связи число ошибок в кодовой последовательности может превышать величину [(d-1)/2] с достаточно большой вероятностью, то реализация режима исправления ошибок может быть бесполезной или даже вредной.

В реальном канале связи часто наблюдается группирование ошибок, когда искажается не один двоичный символ, а целый пакет, длина которого может превышать величину [(d-1)/2]. Это обстоятельство является одной из причин, ограничивающей широкое применение кодов с исправлением ошибок. Для широкого применения кодов с исправлением ошибок такой код в качестве одного из своих свойств должен обеспечивать гарантированную границу для вероятности ошибки декодирования в канале связи с произвольным распределением потока ошибок в канале связи.

Обычно оценка вероятности ошибки декодирования делается для q-ичного симметричного канала при вероятности искажения q-ичного символа P_q. В таком канале с вероятностыо 1 — P_q q-ичный символ принимается верно, после его искажения с вероятностью Р_q каждое значение q-ичного символа отличается от переданного и появляется на входе декодера с одинаковой вероятностью

P_q/(q-1).

В таком канале в зависимости от кратности ошибки t вероятность ошибки декодирования

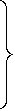
P_ош(t)=0 при t ≤ (d_РС-1)/2 =t_РС

P_ош(t) ≤ (q-1) → ∑ C_n^S (q-1)^S

при d - t_РС ≤ t ≤ d-1

P_ош(t) ≤ (q-1) → ∑ C_n^S (q-1)^S при t ≥d (1)

В канале, не являющемся q-ичным симметричным для кода РС, получены следующие оценки для t>d — t_Pc

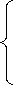1/(q-1)^i-2 + 1/(q-1)ⁱ при t_РС =1

P (t) ≤ (2)

1/(q-1)^i-2t -1/t! при t_РС ≥ 2

При исправлении t_РС ошибок в [9] предлагается оценка

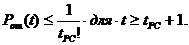(3)

То есть, если кратность ошибки t превосходит исправляющую способность кода tpc, то в канале, не являющемся q-ичным симметричным, вероятность ошибки декодирования не зависит от основания кода q при исправлении tpc ошибок и достаточно близка к единице при малых tpc. Но q-ичный симметричный канал не существует в природе, особенно для больших q, свойство равновероятности (q—1) значений искаженного q-ичного символа для такого канала достигается применением стохастического преобразования q-ичных символов канала.[3]

Защита от ошибок в различных телекоммуникационных системах сводится к применению протоколов, содержащих описание двух основных функций: помехоустойчивого кодирования и управления передачей на конкретном протокольном уровне (для канального, сетевого и сеансового уровней) эталонной модели взаимодействия открытых систем (ЭМВОС). Защита информации в таких системах сводится не только к борьбе с независимыми искажениями в канале связи (в двоичном – симметричном канале ДСК), но и к защите от группирующихся искажений (пакетов ошибок) и от преднамеренных искажений. Выше было показано, что в канале с более сложным распределением потока ошибок, чем в ДСК, применение кодов, исправляющих ошибки, затруднено. Применение кодов с исправлением ошибок преднамеренного характера до последнего времени считалось в принципе невозможным, хотя бы для классических алгебраических кодов.

С учетом сказанного выше, можно сказать, что теория алгебраического кодирования с алгоритмом декодирования по принципу максимального правдоподобия для исправления независимых ошибок является примером того, как ошибочная постановка задачи о независимых ошибках в канале связи сводит практически на нет труды целого поколения исследователей.

Для обеспечения применения кодов, исправляющих ошибки, сформулируем два варианта постановки задачи. [4]

При этом будем учитывать требования к защите информации в современных информационных и телекоммуникационных системах.. Особенностями таких глобальных систем является передача очень больших массивов информации и использование различных каналов связи наиболее простым образом без проведения исследования их свойств, в том числе модели ошибок в них.

Первая постановка, являющаяся «мягкой», состоит в том, что применяемые коды с исправлением ошибок должны обеспечивать в канале с естественными помехами (ошибками) подвергаемую количественной оценке вероятность ошибки декодирования отдельно по следующим характерным интервалам кратности ошибки:

- кратность ошибки t меньше половины величины кодового расстояния d, т.е. t £ [(d-1)/2]

- кратность ошибки t меньше величины кодового расстояния d, т.е. t < d

- кратность ошибки t больше величины кодового расстояния d, t > d³

Вторая постановка, являющаяся сильной, состоит в том, что применяемые коды с исправлением ошибок должны обеспечивать в канале с произвольным характером ошибок гарантированную верхнюю границу для вероятности ошибки декодирование на всем интервале возможной кратности ошибки t £ n; причем эта граница должна устанавливаться при проектировании выбором параметров кода.

Из эвристических соображений сформулируем свойства помехоустойчивого кода с исправлением ошибок, которые позволили бы обеспечить его применение для защиты информации в современных информационных и телекоммуникационных системах в любых из существующих задачах применения.[14]

1. Код имеет режимы обнаружения и исправления ошибок с обеспечением в обоих режимах гарантированной (наперед заданной) вероятности декодирования с ошибкой в произвольном канале связи и надежным отказом от декодирования при невозможности исправления ошибки.

2. Код имеет такую исправляющую способность и позволяет выбрать такие параметры n и k, что использующий их алгоритм передачи информации характеризуется нехудшими вероятностно-временными характеристиками по сравнению с применением альтернативных кодов.

3. Код обеспечивает в режиме исправления ошибок выделение с заданной точностью части правильно принятых символов даже при кратности ошибки, превышающей исправляющую способность кода.

4. Код позволяет декодировать несколько копий (одинаковых по содержанию информации кодовых блоков) блока с эффективностью, превышающей эффективность декодирования исходного кода с обнаружением или исправлением ошибок. Это свойство может применяться для работы по параллельным каналам, при многократной передаче сообщения по одному каналу или в канале с обратной связью при обработке копий после приема повторенного блока.

5. Процедуры кодирования и декодирования кода содержат, в основном, операции по модулю 2.

6. Метод кодирования должен обладать свойствами случайности сигналов на выходе кодера, обеспечивающими совместное решение задач обеспечения помехоустойчивости и секретности в постановке К. Шеннона.

Код Шеннона

Оптимальным кодом можно определить тот, в котором каждый двоичный символ будет передавать максимальную информацию. В силу формул Хартли и Шеннона максимум энтропии достигается при равновероятных событиях, следовательно, двоичный код будет оптимальным, если в закодированном сообщении символы 0 и 1 будут встречаться одинаково часто.[8]

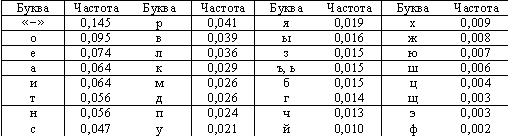
Рассмотрим в качестве примера оптимальное двоичное кодирование букв русского алфавита вместе с символом пробела «-». Полагаем, что известны вероятности появления в сообщении символов русского алфавита, например, приведенные в таблице 3.

Таблица 3.Частота букв русского языка (предположение)

К. Шеннон и Р. Фано независимо предложили в 1948-1949 гг. способ построения кода, основанный на выполнении условия равной вероятности символов 0 и 1 в закодированном сообщении. [10]

Все кодируемые символы (буквы) разделяются на две группы так, что сумма вероятностей символов в первой группе равна сумме вероятностей символов второй группы (то есть вероятность того, что в сообщении встретится символ из первой группы, равна вероятности того, что в сообщении встретится символ из второй группы).

Для символов первой группы значение первого разряда кода присваивается равным «0», для символов второй группы – равными «1».

Далее каждая группа разделяется на две подгруппы, так чтобы суммы вероятностей знаков в каждой подгруппе были равны. Для символов первой подгруппы каждой группы значение второго разряда кода присваивается равным «0», для символов второй подгруппы каждой группы – «1». Такой процесс разбиения символов на группы и кодирования продолжается до тех пор, пока в подгруппах не остается по одному символу.

Пример кодирования символов русского алфавита приведен в табл. 4

Таблица 4. Пример кодирования букв русского алфавита с помощью кода Шеннна-Фано.

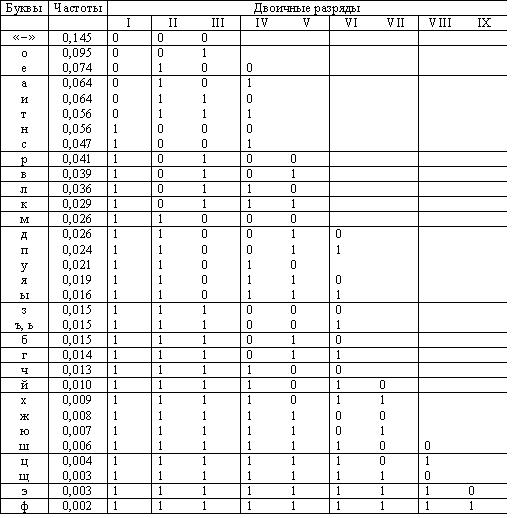
Анализ приведенных в таблице кодов приводит к выводу, что часто встречающиеся символы кодируются более короткими двоичными последовательностями, а редко встречающиеся - более длинными. Значит, в среднем для кодирования сообщения определенной длины потребуется меньшее число двоичных символов 0 и 1, чем при любом другом способе кодирования.

Вместе с тем процедура построения кода Шеннона-Фано удовлетворяет критерию различимости Фано. Код является префиксным и не требует специального символа, отделяющего буквы друг от друга для однозначного него декодирование двоичного сообщения.

Таким образом, проблема помехоустойчивого кодирования представляет собой обширную область теоретических и прикладных исследований. Основными задачами при этом являются следующие: отыскание кодов, эффективно исправляющих ошибки требуемого вида; нахождение методов кодирования и декодирования и простых способов их реализации.

Наиболее разработаны эти задачи применительно к систематическим кодам. Такие коды успешно применяются в вычислительной технике, различных автоматизированных цифровых устройствах и цифровых системах передачи информации.