Радиальная фильтрация нефти и газа в пористой среде
Процесс притока пластовых флюидов из пласта в скважину описывается моделью радиальной фильтрации. В этом случае образец породы представляется в виде цилиндрического кольца с проводящими каналами в осевом направлении (рис. 1.7).
 скважина
скважина
| Рис. 1.7. Схема радиального притока жидкости в скважину |
нефтяной пласт
Площадь боковой поверхности цилиндра: F=2πrh, таким образом уравнение Дарси для радиальной фильтрации будет иметь следующий вид:

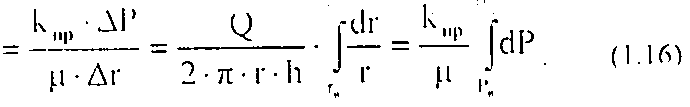
Отсюда дебит при радиальной фильтрации жидкости:
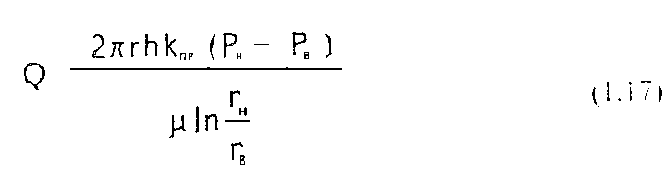
Таким образом, коэффициент проницаемости при радиальной фильтрации:
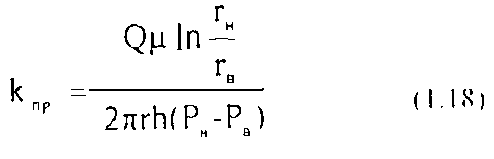
1.2.3. Оценка проницаемости пласта, состоящего из нескольких пропластков различной проницаемости
Пласт состоит, как правило, из отдельных пропластков, поэтому общая проницаемость пласта (кпр) оценивается с учетом проницаемости пропластков и направления фильтрации.
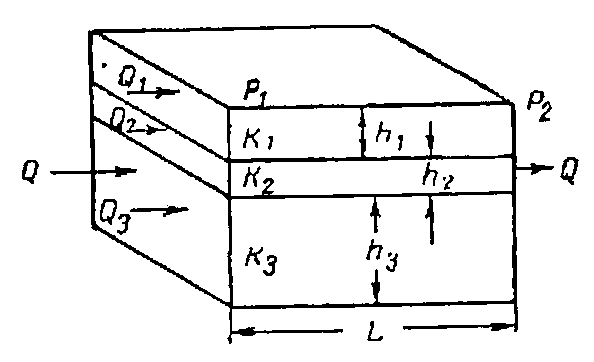
Рис.1.8 Линейная фильтрация в пласте, состоящем из нескольких изолированных пропластков различной мощности и проницаемости.
При линейной фильтрации жидкости в пласте, состоящем из нескольких однофазных пропластков различной мощности и проницаемости (рис. 1.8), общая проницаемость пласта рассчитывается следующим образом:
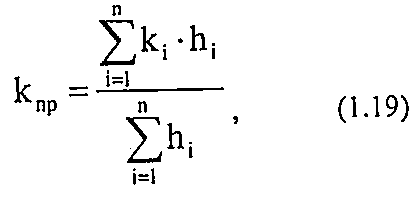
Где: hi—мощность i-го пропластка
ki - проницаемость i-ro пропластка.
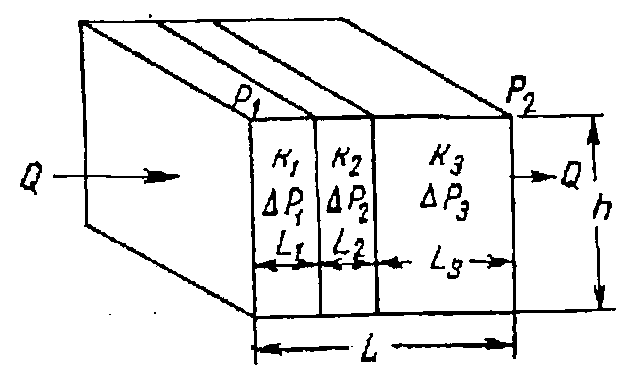
Рис 1.9. Линейная фильтрация через пласт, имеющий несколько последовательно расположенных зон различной проницаемости
При линейной фильтрации жидкости через пласт, имеющий несколько последовательно расположенных зон различной проницаемости (рис. 1.9), коэффициент проницаемости пласта рассчитывается следующим образом:
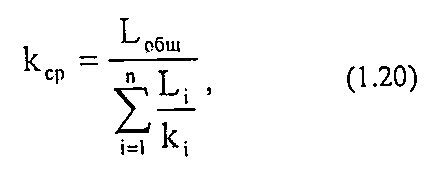
где Li - длина i-гo пропластка;
ki - проницаемость i-гo пропластка.
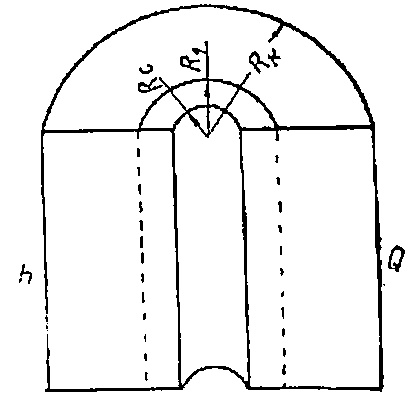
Рис. 1.10. Радиальная фильтрация через пласт, имеющий несколько концентрически расположенных зон различной проницаемости.
При радиальной фильтрации жидкости через пласт, имеющий несколько концентрически расположенных зон различной проницаемости (рис. 1.10), средняя проницаемость пласта оценивается следующим образом:
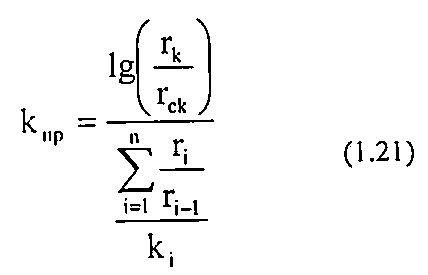
где гк - радиус контура;
гс - радиус скважины;
гi - радиус i-гo пропластка;
kj - проницаемость i-гo пропластка.
1.3.4. Классификация проницаемых пород
По характеру проницаемости (классификация Теодоровича Г.И.) различают коллектора:
- равномерно проницаемые;
- неравномерно проницаемые;
- трещиноватые.
По величине проницаемости (мкм2) для нефти выделяют 5 классов коллекторов:
1. очень хорошо проницаемые (>1);
2. хорошо проницаемые (0,1 - 1);
3. средне проницаемые (0,01 - 0,1);
4. слабопроницаемые (0,001 -0,01);
5. плохопроиицаемые (<0,001).
Для классификации коллекторов газовых месторождений используют классы коллекторов.
1.3.5. Зависимость проницаемости от пористости
Теоретически, для хорошо отсортированного материала (песок мономиктовый) проницаемость не зависит от пористости.
Для реальных коллекторов в общем случае более пористые породы являются болеепроницаемыми.
Зависимость проницаемости от размера пор для фильтрации через капиллярные поры идеально пористой среды оценивается из соотношения уравнений Пуазейля и Дарси. В этом случае пористая среда представляется в виде системы прямых трубок одинакового сечения длиной L, равной длине пористой среды.
Уравнение Пуазейля описывает объёмную скорость течения жидкости через такую пористую среду:
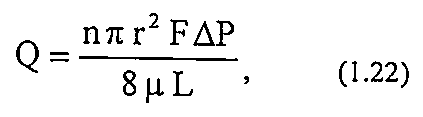
где г - радиус порового канала;
L-длина порового канала;
n - число пор, приходящихся на единицу площади фильтрации;
F - площадь фильтрации;
µ- вязкость жидкости;
∆Р - перепад давлений,
Коэффициент пористости среды, через которую проходит фильтрация:
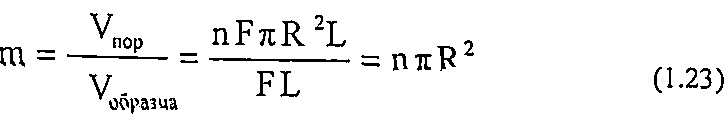
Следовательно, уравнение (1.22) можно переписать следующим образом:
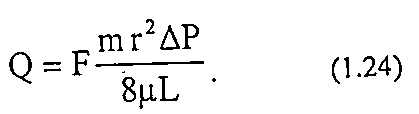
Из уравнения Дарси следует, что:

Приравняв правые части уравнений (1.24) и (1.25) получим взаимосвязь пористости и проницаемости:
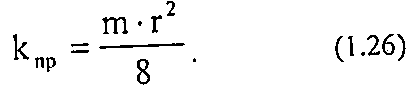
Из чего следует, что размер порового канала будет равен:
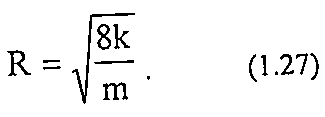
Если выразить проницаемость в мкм2, то радиус поровых каналов (в мкм) будет равен:
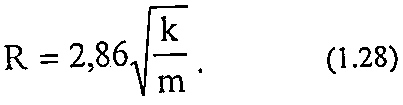
Оценка проницаемости для фильтрации через трещиноватые поры оценивается из соотношения уравнений Букингема и Дарси.
Потери давления при течении жидкости через щель очень малой высоты оцениваются уравнением Букингема:

где h - высота трещины;
v - линейная скорость фильтрации.
Подставив это выражение в уравнение Дарси, получим:
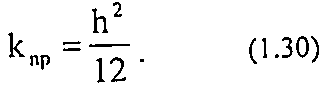
Соотношения (1.25) и (1.26) справедливы только для идеальной пористой среды (например, кварцевый песок).
Для реальных условий используется эмпирическое уравнение Котяхова:
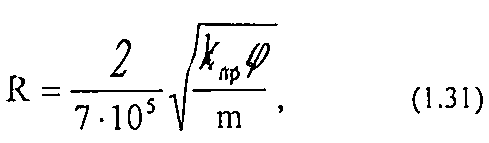
где R- радиус пop;
φ - структурный коэффициент, описывающий извилистость порового пространства.
Значение φ можно оценить путём измерения электросопротивления пород. Для керамических пористых сред при изменении пористости от 0,39 до 0,28, по экспериментальным данным, φ изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно оценить по эмпирической формуле:
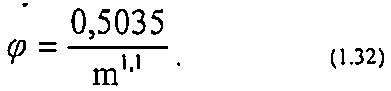
Виды проницаемости
Проницаемость абсолютная (физическая) - проницаемость пористой среды для газа или однородной жидкости при следующих условиях:
1. Отсутствие физико-химического взаимодействия между пористой
средой и этим газом или жидкостью.
2. Полное заполнение всех пор среды этим газом или жидкостью.
Для продуктивных нефтяных пластов эти условия не выполняются.
Проницаемость фазовая (эффективная) - проницаемость пористой среды для данного газа или жидкости при одновременном наличии в порах другой фазы или системы (газ-нефть, газ-нефть-вода).
При фильтрации смесей коэффициент фазовой проницаемости намного меньше абсолютной проницаемости и неодинаков для пласта в целом.
Относительная проницаемость - отношение фазовой проницаемости к
абсолютной.
Проницаемость горной породы зависит от степени насыщения породы флюидами, соотношения фаз, физико-химических свойств породы и флюидов.
Фазовая и относительная проницаемости для различных фаз зависят от нефте-, газо- и водонасыщенности порового пространства породы, градиента давления, физико-химических свойств жидкостей и пористых фаз.
Насыщенность- ещё один важный параметр продуктивных пластов, тесно связанный с фазовой проницаемостью.
Предполагается, что продуктивные пласты сначала были насыщены водой. Водой были заполнены капилляры, трещины, каналы.
При миграции углеводороды, вследствие меньшей плотности, стремятся верхней части пласта, выдавливая вниз воду. Вода легче всего уходит из трещин и каналов, из капилляров вода не уходит в силу капиллярных явлений. Таким образом, в пласте остаётся связанная вода.
Чтобы определить количество углеводородов, содержащихся в продуктивном пласте необходимо определить насыщенность порового пространства породы нефтью, водой и газом.
Водонасыщенность SВ - отношение объёма открытых пор, заполненных водой к общему объёму пор горной породы. Аналогично определение нефте- и газонасыщенности:
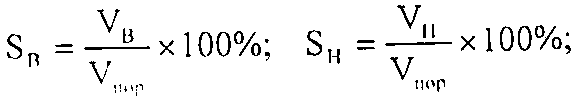
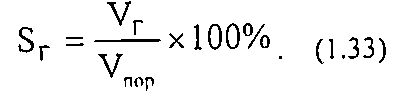
Обычно для нефтяных месторождений SВ = 6-35%; SН = 65-94%. в зависимости от созревания пласта.
Для нефтяных месторождений справедливо следующее соотношение:

Для газонефтяных месторождений:
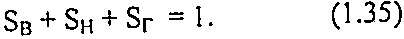
Пласт считается созревшим для разработки, если остаточная водонасыщенность SВ<25%
Остаточная водонасыщенность. обусловленная капиллярными силами, не влияет на основную фильтрацию нефти и газа.
При водонасыщенности до 25% нефте- и газонасыщенность пород максимальная: 45-77%, а относительная фазовая проницаемость для воды равна нулю.
При увеличении водонасыщенности до 40%, фазовая проницаемость для нефти и газа уменьшается в 2-2,5 раза. При увеличении водонасыщенности до 80% фильтрация газа и нефти в пласте стремится к нулю.
Экспериментально изучался поток при одновременном содержании в пористой среде нефти, воды и газа. Опытами установлено, что в зависимости от объемного насыщения порового пространства различными компонентами возможно одно-, двух- и трёхфазное движение. Результаты исследования представлены в виде треугольной диаграммы (рис. 1.11).
Вершины треугольника соответствуют стопроцентному насыщению породы одной из фаз; стороны, противолежащие вершинам, - нулевому насыщению породы этой фазой. Кривые, проведённые на диаграмме, ограничивают возможные области одно-, двух-, и трёхфазного потока.
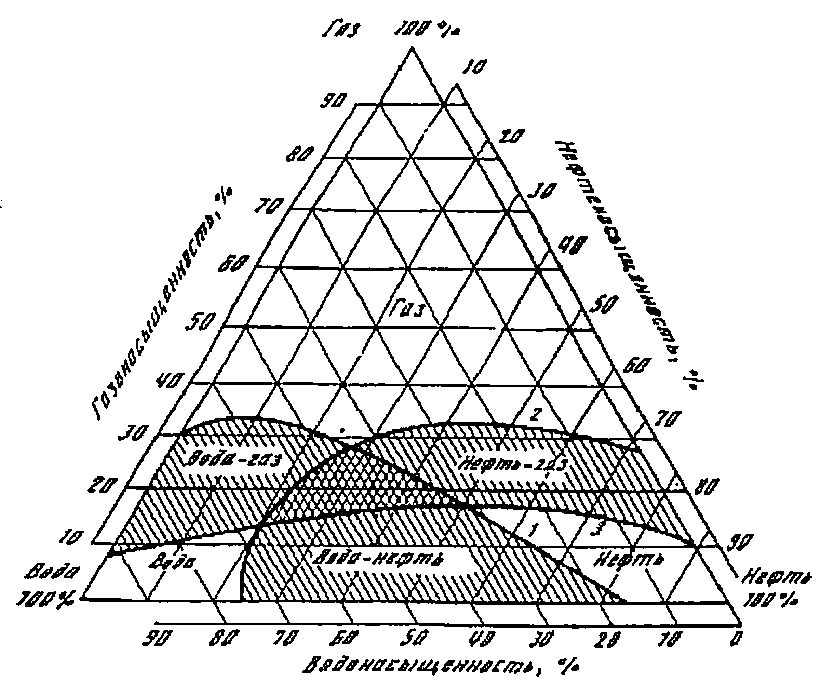
Рис 1.11. Области распространения одно-, двух- и трехфазного потоков:
1. – 5% воды; 2. – 5% нефти; 3. – 5% газа.
2. МЕХАНИЧЕСКИЕ И ТЕПЛОВЫЕ СВОЙСТВА ПОРОД
2.1. МЕХАНИЧЕСКИЕ СВОЙСТВА ГОРНЫХ ПОРОД
Упругость, прочность на сжатие и разрыв, пластичность - наиболее важные механические свойства горных пород, влияющие на ряд процессов, происходящих в пласте в период разработки и эксплуатации месторождений.
Упругие свойства горных пород и влияют на перераспределения давления в пласте в процессе эксплуатации месторождения. Давление в пласте, благодаря упругим свойствам пород, перераспределяется не мгновенно, а постепенно после изменения режима работы скважины.
Упругость - свойство горных пород сопротивляться изменению их объёма и формы под действием приложенных сил. Абсолютно упругое тело восстанавливает первоначальную форму мгновенно после снятия напряжения. Если тело не восстанавливает первоначальную форму или восстанавливает её в течение времени, то оно называется пластичным.
2.2. ТЕПЛОВЫЕ СВОЙСТВА ГОРНЫХ ПОРОД
Тепловые свойства горных пород характеризуются удельной теплоёмкостью, коэффициентом температуропроводности и коэффициентом теплопроводности.
Удельная (массовая)теплоёмкость характеризуется количеством теплоты, необходимым для нагрева единицы массы породы на 1°С:
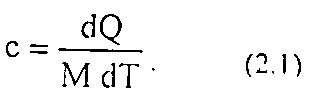
Этот параметр необходимо учитывать при тепловом воздействии на пласт.
Коэффициент теплопроводности (удельного теплового сопротивления) λ характеризует количество теплоты dQ, переносимой в породе через единицу площади S в единицу времени t при градиенте температуры dT/dx:
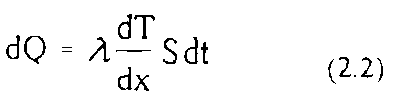
Коэффициент температуропроводности характеризует, скорость прогрева пород (или скорость распространения изотермических границ):
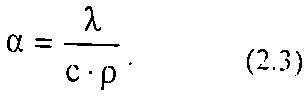
Коэффициенты линейного (aL) и объёмного (аv) расширения характеризуют изменение размеров породы при нагревании:
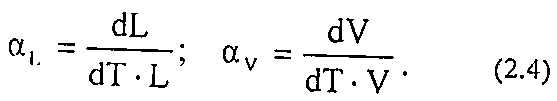
Теплоёмкость пород зависит от минералогического состава пород и не зависит от строения и структуры минералов. Удельная теплоёмкость увеличивается при уменьшении плотности породы и растёт с увеличение температуры и влажности в пределах 0,4-2 кДж/(кг-К).
Теплопроводность и температуропроводность пород очень низки по сравнению с металлами. Поэтому для прогрева призабойных зон требуется очень большая мощность нагревателей. Вдоль напластования теплопроводность выше, чем поперёк напластования на 10-50%.
Коэффициенты линейного и объёмного расширения изменяются в зависимости от плотности породы аналогично теплоёмкости. Наибольшим значением коэффициентов расширения обладает кварцевый песок и другие крупнозернистые породы.
Коэффициент линейного расширения пород уменьшается с ростом плотности минералов.
Тепловые свойства некоторых горных пород и пластовых флюидов
Таблица 2.1
| Горная порода | с, кДж/(кг-К) | λ, Вт/(м-К) | а-103, м2/с | aL-105, 1/К | ||
| Глина | 0,755 | 0,99 | 0,97 | - | ||
| Глинистые сланцы | 0,772 | 154-218 | 0,97 | 0,9 | ||
| Доломит | 0,93 | 1,1-4,98 | 0,86 | - | ||
| Известняк | 1,1 | 2,18 | 0,91 | 0,5-0,89 | ||
| Кварц | 0,692 | 2,49 | 1,36 | 1,36 | ||
| Песок | 0,8 | 0,347 | 0,2 | 0,5 | ||
| Пластовые флюиды | с, кДж/(кг-К) | λ, Вт/(м-К) | а-103, м2/с | aL-105, 1/К | ||
| Нефть | 2,1 | 0,139 | 0,069-0,086 | — | ||
| Газ | 4,15 | 0,582 | 0,14 | - | ||
Дата добавления: 2016-03-22; просмотров: 3692;
