Обмеження моделі Мальтуса. Логістичне рівняння, його розв’язок. Висновки з розв’язку логістичного рівняння.
Пригадаємо виведену нами на минулому занятті математичну модель Мальтуса. Вона починалась з припущення, що швидкість зростання чисельності популяції пропорційна її чисельності.
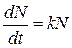
Це припущення привело нас до кінцевої формули 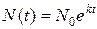 , що описувала закономірність зміни чисельності деяких реальних колоній до виснаження запасів їжі. Тоді ми вже зазначали, що насправді через численні причини вона описує динаміку небагатьох популяцій і лише на досить обмеженій стадії їх розвитку. Дійсно, тут зовсім не враховано навіть той факт, що всередині популяції навіть при відсутності смертності і зовнішніх хижаків, виникає внутрішня конкуренція за їжу. Чим численніша молочнокислих бактерій, тим гостріша внутрішня боротьба за їжу. На пізніших стадіях розвитку вона навіть може зупинити зростання популяції. Цей ефект спостерігається навіть у відсутності природних ворогів, коли жодна популяція не розвиваються безмежно. Такий ефект називається ефектом самоотруєння популяцій.
, що описувала закономірність зміни чисельності деяких реальних колоній до виснаження запасів їжі. Тоді ми вже зазначали, що насправді через численні причини вона описує динаміку небагатьох популяцій і лише на досить обмеженій стадії їх розвитку. Дійсно, тут зовсім не враховано навіть той факт, що всередині популяції навіть при відсутності смертності і зовнішніх хижаків, виникає внутрішня конкуренція за їжу. Чим численніша молочнокислих бактерій, тим гостріша внутрішня боротьба за їжу. На пізніших стадіях розвитку вона навіть може зупинити зростання популяції. Цей ефект спостерігається навіть у відсутності природних ворогів, коли жодна популяція не розвиваються безмежно. Такий ефект називається ефектом самоотруєння популяцій.
Ще раз підкреслимо, що рівняння Мальтуса може бути застосовано з певними обмеженнями і лише для колоній, в яких особини не вмирають (діляться раніше настання смерті).
Для популяцій, які знаходяться лише під дією обмеженості їжі вихідне рівняння записують в дещо зміненому вигляді:
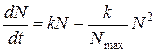 , (*)
, (*)
де N – чисельність популяції в даний момент часу, Nmax – максимальна чисельність популяції, що може існувати в даних умовах, k – константа швидкості зростання популяції. Другий член даного рівняння і враховує дію ефекту самоотруєння популяції.
Наведене рівняння носить назву логістичногоі було вперше запропоноване Ферхюльстом в 1838 році. Згодом про нього забули і через 100 років воно було заново відкрите Лотка, Перлом і Рідом. Цікаво, що останні два автори вже ввели це рівняння безпосередньо для опису динаміки зростання населення США.
Логістичне рівняння (*) можна переписати в іншому вигляді:
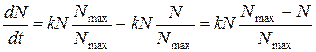
Розділимо змінні:
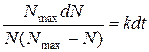 (*)
(*)
Вираз, що входить до лівої частини 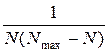 може бути переписаний у вигляді (змінна – N, Nmax – константа):
може бути переписаний у вигляді (змінна – N, Nmax – константа):
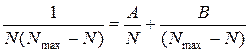 (**)
(**)
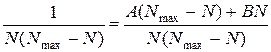
Тут А і В – невизначені поки що коефіцієнти, які можна знайти виходячи із того, що ліва і права частина цієї рівності однакові, знаменники теж однакові, тому чисельники лівої і правої частини теж повинні бути однакові. Запишемо рівність чисельників.
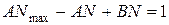
Справа відсутня змінна N, тому можна записати:
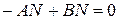
і
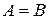
З аналогічних міркувань:
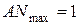
і
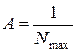
Використовуючи знайденні значення А і В, а також вираз (**) ми можемо переписати (*) у вигляді:
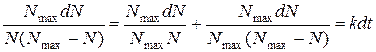
Тобто
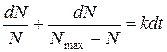
Проінтегруємо цей вираз:
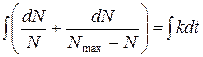
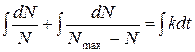
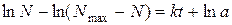
Тут lnа – стала інтегрування. Останнє спрощення приводить нас до виразу:
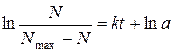
Звідки
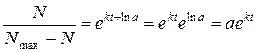
Знову розглянемо початкові умови, коли 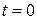 і
і 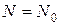 .
.
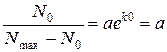
Розв’яжемо попереднє рівняння відносно N:
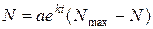
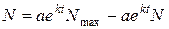
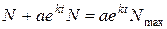
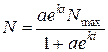
В отриманому рівнянні розділимо чисельник і знаменник на 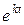 :
:
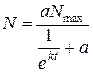
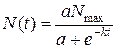 (***)
(***)
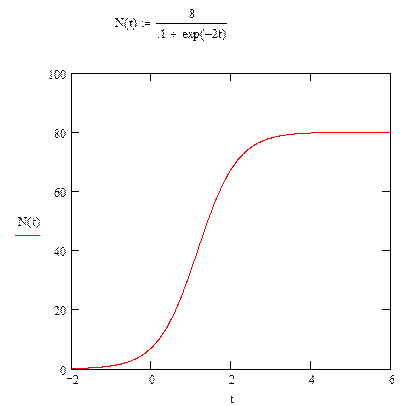 Це рівняння описує залежність чисельності популяцій в залежності від часу і при умові дії внутрішньої конкуренції в популяції (самоотруєння популяції). Графічно воно описується вже відомою нам сигмовидною лінією. Вона також називається логістичною кривою. На практичних заняттях ми побудуємо цю функцію і побачимо, що вона дійсно має такий вигляд. Можна побачити, що логістична крива ніби складається з двох – з експоненційної (перша частина) і оберненої експоненційної (друга частина) кривих. Якщо проаналізувати поведінку логістичної кривої при зміні значень t від о до безмежності, ми побачимо, що система, яка описується даною кривою починає розвиток з певної початкової чисельності. Далі починається повільне зростання чисельності, яке сягає максимальної швидкості при N=Nmax. Після досягнення цього значення починається гальмування розвитку. Чим ближче підходить чисельність системи до максимальної, тим повільніше вона зростає. Врешті, зростання практичне припиняється і чисельність системи вже практично співпадає з максимальною. За умови неускладненого розвитку у відсутності хижаків, хвороб, тиску антропогенних факторів реальні природні системи розвиваються саме за таким сценарієм. Важливість цієї моделі для галузі харчових технологій полягає в тому, що певні біотехнологічні процеси добре описуються нею. Отже, можна наприклад з’ясувати питання про те, коли чисельність молочнокислих бактерій досягне необхідного (або максимального) рівня і подальше перебування продукту у реакторі для дозрівання колонії стане непотрібним. Приблизну оцінку часу за такою моделлю можна зробити розрахунково, без жодних мікробіологічних досліджень.
Це рівняння описує залежність чисельності популяцій в залежності від часу і при умові дії внутрішньої конкуренції в популяції (самоотруєння популяції). Графічно воно описується вже відомою нам сигмовидною лінією. Вона також називається логістичною кривою. На практичних заняттях ми побудуємо цю функцію і побачимо, що вона дійсно має такий вигляд. Можна побачити, що логістична крива ніби складається з двох – з експоненційної (перша частина) і оберненої експоненційної (друга частина) кривих. Якщо проаналізувати поведінку логістичної кривої при зміні значень t від о до безмежності, ми побачимо, що система, яка описується даною кривою починає розвиток з певної початкової чисельності. Далі починається повільне зростання чисельності, яке сягає максимальної швидкості при N=Nmax. Після досягнення цього значення починається гальмування розвитку. Чим ближче підходить чисельність системи до максимальної, тим повільніше вона зростає. Врешті, зростання практичне припиняється і чисельність системи вже практично співпадає з максимальною. За умови неускладненого розвитку у відсутності хижаків, хвороб, тиску антропогенних факторів реальні природні системи розвиваються саме за таким сценарієм. Важливість цієї моделі для галузі харчових технологій полягає в тому, що певні біотехнологічні процеси добре описуються нею. Отже, можна наприклад з’ясувати питання про те, коли чисельність молочнокислих бактерій досягне необхідного (або максимального) рівня і подальше перебування продукту у реакторі для дозрівання колонії стане непотрібним. Приблизну оцінку часу за такою моделлю можна зробити розрахунково, без жодних мікробіологічних досліджень.
Принципово важливою тут є точка перетину, після якої крива проходить максимальну швидкість зростання і починає нахилятись ближче до горизонтальної вісі. Фактично у цій точці наша модель відходить від моделі Мальтуса. Ця точка відповідає кількості популяції в ½ Nmax. Важливим є час досягнення цієї точки. Його можна розрахувати, підставивши в рівняння (***) замість N(t) значення ½ Nmax. Для того, щоб не переобтяжувати себе, на практичному занятті ми залучимо маткад до спрощення отриманого рівняння, яке поки що наведемо без доказу:
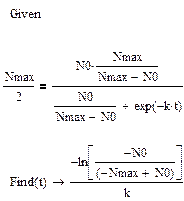 |
Дещо спростивши результат можна записати:
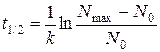
Таким буде час досягнення максимальної швидкості розмноження, після якого починається гальмування розвитку популяції.
Зробимо висновки з розв’язку і початкового аналізу логістичного рівняння:
1. Логістичне рівняння адекватно описує цілісний процес розвитку реальних природних популяцій, що існують при стабільних і сприятливих зовнішніх умовах. Воно дозволяє точніше розрахувати чисельність популяції на будь-якому етапі від початку зростання до насичення.
2. При малих чисельностях популяцій їх динаміка добре описується простим експоненціальним законом (рівнянням Мальтуса), при великих – оберненим рівнянням Мальтуса. Для цілісного опису необхідне об’єднане рівняння – логістичне.
3. Ще раз підкреслимо, що аналогічними рівняннями описуються не тільки динаміка популяцій, але й багато інших, наприклад соціальних процесів.
4. Максимальний рівень чисельності популяції досягається тим швидше, чим більшою є константа швидкості розмноження популяції k.
5. Ця ж константа визначає час досягнення максимальної швидкості розмноження популяції.
Таким чином сьогодні ми отримали вже цілком адекватну модель для опису багатьох реальних природних процесів. З її використанням можна коректно моделювати перебіг багатьох природних процесів, що ми й будемо робити на наступних практичних заняттях.
Приклад побудови логістичної кривої у Excel і з находження часу досягнення точки перетину:
Дано:
Початкова чисельність популяції: 50 особин, максимальна – 2000 особин, часова константа швидкості розмноження = 1,7.
Завдання: побудувати графік змін чисельності популяції і знайти час досягнення точки перетину на цьому графіку.
| Поч чис | Час | Поточ чис | Макс чис | Константа а | Константа к |
| N0 | t | N(t) | Nmax | a | k |
| 0,025641026 | 1,7 | ||||
| 0,1 | 58,99196 | 0,025641026 | 1,7 | ||
| 0,2 | 69,54334 | 0,025641026 | 1,7 | ||
| 0,3 | 81,90234 | 0,025641026 | 1,7 | ||
| 0,4 | 96,3481 | 0,025641026 | 1,7 | ||
| 0,5 | 113,1914 | 0,025641026 | 1,7 | ||
| 0,6 | 132,7739 | 0,025641026 | 1,7 | ||
| 0,7 | 155,465 | 0,025641026 | 1,7 | ||
| 0,8 | 181,6568 | 0,025641026 | 1,7 | ||
| 0,9 | 211,7547 | 0,025641026 | 1,7 | ||
| 246,1642 | 0,025641026 | 1,7 | |||
| 1,1 | 285,2732 | 0,025641026 | 1,7 | ||
| 1,2 | 329,4285 | 0,025641026 | 1,7 | ||
| 1,3 | 378,9081 | 0,025641026 | 1,7 | ||
| 1,4 | 433,8891 | 0,025641026 | 1,7 | ||
| 1,5 | 494,415 | 0,025641026 | 1,7 | ||
| 1,6 | 560,3629 | 0,025641026 | 1,7 | ||
| 1,7 | 631,4183 | 0,025641026 | 1,7 | ||
| 1,8 | 707,0585 | 0,025641026 | 1,7 | ||
| 1,9 | 786,5523 | 0,025641026 | 1,7 | ||
| 868,9768 | 0,025641026 | 1,7 | |||
| 2,1 | 953,2533 | 0,025641026 | 1,7 | ||
| 2,2 | 1038,201 | 0,025641026 | 1,7 | ||
| 2,3 | 1122,599 | 0,025641026 | 1,7 | ||
| 2,4 | 1205,261 | 0,025641026 | 1,7 | ||
| 2,5 | 1285,095 | 0,025641026 | 1,7 | ||
| 2,6 | 1361,16 | 0,025641026 | 1,7 | ||
| 2,7 | 1432,704 | 0,025641026 | 1,7 | ||
| 2,8 | 1499,184 | 0,025641026 | 1,7 | ||
| 2,9 | 1560,265 | 0,025641026 | 1,7 | ||
| 1615,805 | 0,025641026 | 1,7 | |||
| 3,1 | 1665,833 | 0,025641026 | 1,7 | ||
| 3,2 | 1710,513 | 0,025641026 | 1,7 | ||
| 3,3 | 1750,116 | 0,025641026 | 1,7 | ||
| 3,4 | 1784,981 | 0,025641026 | 1,7 | ||
| 3,5 | 1815,495 | 0,025641026 | 1,7 | ||
| 3,6 | 1842,062 | 0,025641026 | 1,7 | ||
| 3,7 | 1865,088 | 0,025641026 | 1,7 | ||
| 3,8 | 1884,966 | 0,025641026 | 1,7 | ||
| 3,9 | 1902,069 | 0,025641026 | 1,7 | ||
| 1916,742 | 0,025641026 | 1,7 | |||
| 4,1 | 1929,298 | 0,025641026 | 1,7 | ||
| 4,2 | 1940,02 | 0,025641026 | 1,7 | ||
| 4,3 | 1949,158 | 0,025641026 | 1,7 | ||
| 4,4 | 1956,936 | 0,025641026 | 1,7 | ||
| 4,5 | 1963,545 | 0,025641026 | 1,7 | ||
| 4,6 | 1969,157 | 0,025641026 | 1,7 | ||
| 4,7 | 1973,916 | 0,025641026 | 1,7 | ||
| 4,8 | 1977,949 | 0,025641026 | 1,7 | ||
| 4,9 | 1981,364 | 0,025641026 | 1,7 | ||
| 1984,254 | 0,025641026 | 1,7 | |||
| 5,1 | 1986,7 | 0,025641026 | 1,7 |
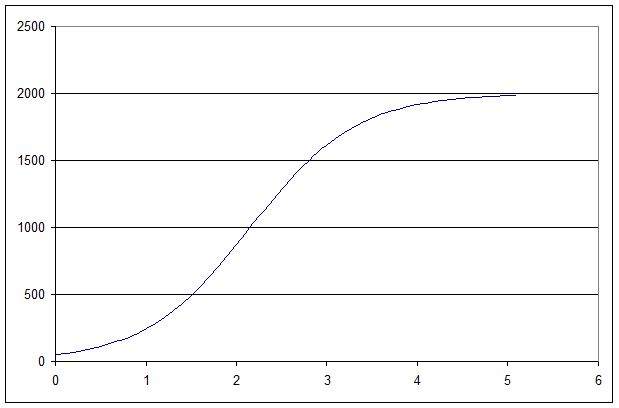
| t1/2= | 2,155036 |
Контрольні завдання
Варіант 1
Початкова чисельність популяції: 5 млн особин, максимальна – 210 млн особин, часова (добова) константа швидкості розмноження = 1,78.
Завдання: побудувати графік змін чисельності популяції і знайти час досягнення точки перетину на цьому графіку. Визначити, коли чисельність популяції досягне 90 % від максимальної.
Варіант 2
Початкова чисельність популяції: 5,9 млн особин, максимальна – 280 млн особин, часова (добова) константа швидкості розмноження = 2,178.
Завдання: побудувати графік змін чисельності популяції і знайти час досягнення точки перетину на цьому графіку. Визначити, коли чисельність популяції досягне 80 % від максимальної.
Варіант 3
Початкова чисельність популяції: 4 млн особин, максимальна – 225 млн особин, часова (добова) константа швидкості розмноження = 2,81.
Завдання: побудувати графік змін чисельності популяції і знайти час досягнення точки перетину на цьому графіку. Визначити, коли чисельність популяції досягне 75 % від максимальної.
Варіант 4
Початкова чисельність популяції: 9 млн особин, максимальна – 2 млрд особин, часова (добова) константа швидкості розмноження = 2,8.
Завдання: побудувати графік змін чисельності популяції і знайти час досягнення точки перетину на цьому графіку. Визначити, коли чисельність популяції досягне 90 % від максимальної.
Варіант 5
Початкова чисельність популяції: 8,5 млн особин, максимальна – 1,1 млрд особин, часова (добова) константа швидкості розмноження = 2,2.
Завдання: побудувати графік змін чисельності популяції і знайти час досягнення точки перетину на цьому графіку. Визначити, коли чисельність популяції досягне 80 % від максимальної.
| <== предыдущая лекция | | | следующая лекция ==> |
| Особливості проведення музейних природничих екскурсій. | | | Творчество А. С. Пушкина 30-х годов. |
Дата добавления: 2016-03-15; просмотров: 1849;
