ТЕОРЕМА КОМПЕНСАЦИИ

В любой электрической цепи без изменения в ней токораспределения резистор может быть заменён ЭДС, численно равной падению напряжения в заменённом резисторе и направленной встречно току в этом резисторе.

Для доказательства теоремы компенсации выделим из схемы одну ветвь с резистором сопротивления R, по которой течет ток I, а всю остальную часть схемы условно обозначим прямоугольником (рис. 1-19, а):

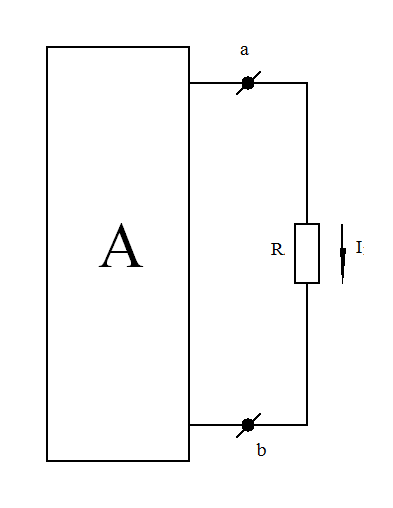
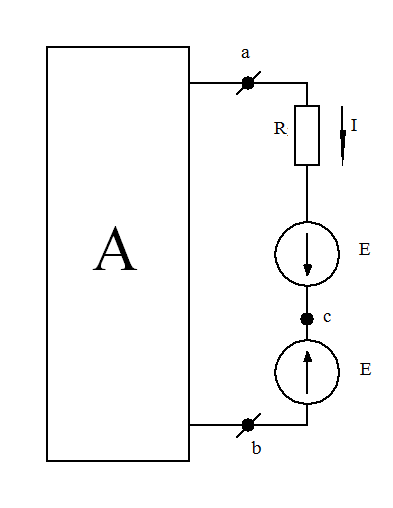
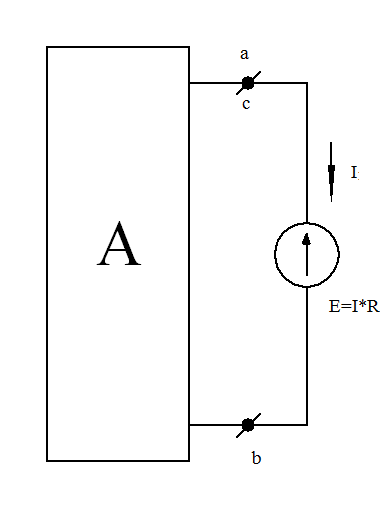
а) б) в)

Рис. 1-19. К доказательству теоремы компенсации

Если в выделенную ветвь включить две равных и противоположно направленных ЭДС Е, численно равных падению напряжения в сопротивлении R резистора от тока I (рис. 1-19,б)

E=I*R, (1-37)

то ток I в цепи от этого не изменится. Убедимся в том, что разность потенциалов между точками «а» и «с» в схеме при этом будет равна нулю.

Действительно,

φ_с = φ_а – IR + Е = φ_а – IR + IR = φ_а . (1-38)

Но если φ_с = φ_а , то точки «а» и «с» можно объединить в одну точку или, другими словами, закоротить участок «ас» и получить схему рис.1-19 в). В ней вместо резистора сопротивлением R включена ЭДС Е.

Убедимся в тождественности схем рис. 1-19, а и 1-19, в

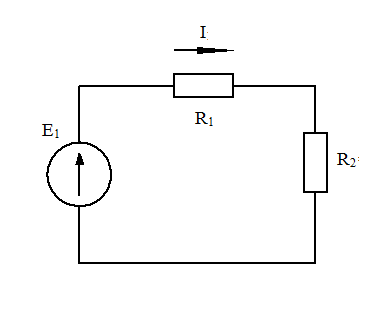
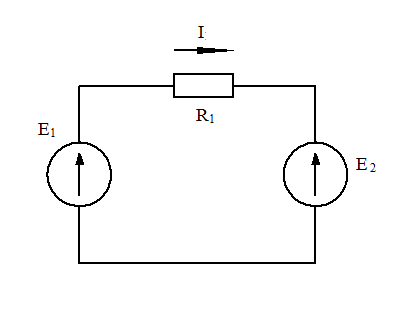а) б)

Рис. 1-20. Тождественность схемы

В схеме рис. 1-20, а ток I = 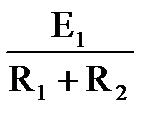. Для схемы рис. 1-20,б ток равен I = 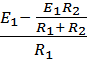= = 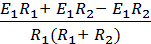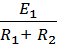. (1-39)

Таким образом, замена сопротивления 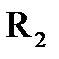на ЭДС Е₂ = IR₂ в схеме

рис. 1-20,б, как это и следует из теоремы компенсации, не вызвала изменения тока в схеме.