МЕТОД КОНТУРНЫХ ТОКОВ

Как показал Максвелл ещё в 1873 году, число уравнений для расчёта токов и напряжений в цепи может быть уменьшено, если составлять их только по одному из законов Кирхгофа, то есть только для контуров или только для узлов.

Ток в любой ветви электрической цепи всегда можно представить составленным из нескольких токов, каждый из которых замыкается по своему контуру, оставаясь вдоль него неизменным. Такие составляющие действительных токов называют контурными токами. Ток в любой ветви, принадлежащий только одному контуру, совпадает с контурным током. Ток в ветви, принадлежащей двум или нескольким контурам, равен алгебраической сумме соответствующих контурных токов.

Контурные токи, проходя через узел, остаются непрерывными, следовательно, первый закон Кирхгофа выполняется автоматически. Поэтому уравнения с контурными токами составляются только по второму закону Кирхгофа. Число таких независимых уравнений равно числу независимых контуров. Рассмотрим метод контурных токов на схеме рис. 1-21.

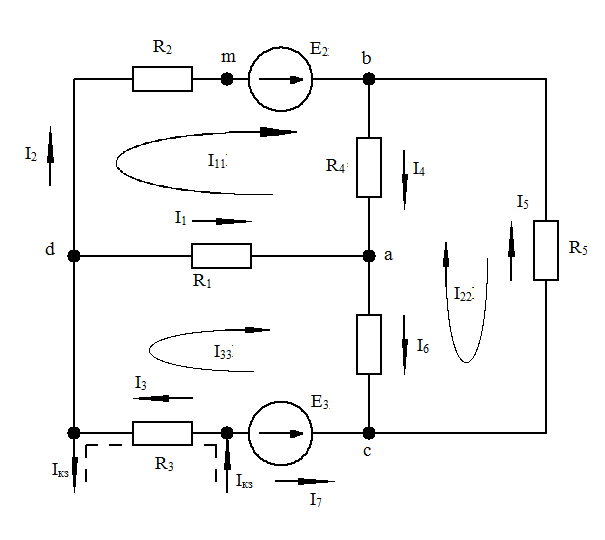
Рис. 1-21. Схема электрической цепи

В схеме рис. 1-21 число ветвей В равно семи, число узлов У равно пяти.

Число уравнений, которые нужно составить по второму закону Кирхгофа

К₂ = В – (У – 1) = 7 – (5 – 1) = 3.

Число независимых контуров К_нк в данной схеме так же равно трём:

К_нк = 3.

Это и будет число уравнений, которые нужно составить для расчёта токов по методу контурных токов:

К_мкт = К₂ = К_нк = 3.

Выберем произвольно независимые контуры, например, контуры admba, acnda, abca.

Так же произвольно выберем направления контурных токов, например по часовой стрелке на схеме рис. 1-21.

Система контурных уравнений в наиболее общем случае, то есть когда в схеме имеются источники ЭДС и источники тока, имеет следующий вид:

I₁₁R₁₁ + I₂₂R₁₂ + I₃₃R₁₃ + I_КЗR_1K = E₁₁;

I₁₁R₂₁ + I₂₂R₂₂ + I₃₃R₂₃ + I_КЗR_2K = E₂₂; (1-40)

I₁₁R₃₁ + I₂₂R₃₂ + I₃₃R₃₃ + I_КЗR_3K = E₃₃.

Здесь R_kk – суммарное сопротивление к-ого контура;

R₁₁ = R₁ + R₂ + R₄ – суммарное сопротивление первого контура;

R₂₂ = R₄ + R₅ + R₆ – суммарное сопротивление второго контура ;

R₃₃= R₁ + R₃ + R₆ – суммарное сопротивление третьего контура;

Rkn = Rnk - взаимное сопротивление между к-ым и n-ым контурами.

Знак взаимного сопротивления берётся положительным, если контурные токи на этой ветви совпадают, и отрицательным – если не совпадают.

Запишем все взаимные сопротивления:

R₁₂ = R₂₁ = - R₄; R₁₃ = R₃₁ = - R₁; R₂₃ = R₃₂ = - R₆.

R_1k, R_2k, R_3k – это сопротивление первого, второго или третьего контуров соответственно, по которым замыкается ток от источника тока.

Перед написанием этих сопротивлений необходимо выбрать путь, по которому замыкается ток от источника тока I_кз. С целью некоторой экономии времени расчета выберем кратчайший путь через резистор R₃ третьего контура. Этот путь на схеме рис. 1-21 обозначим штриховой линией.

По сколько в первом и втором контурах нет резисторов, по которым замыкается ток от источника тока I_кз, то R_1k = R_2k = 0. И только в третьем контуре есть резистор R₃, по которому замыкается ток от источника тока I_кз.

Это сопротивление берётся положительным, если контурный ток и ток от источника тока на этом резисторе совпадают, и отрицательным – если не совпадает.

В нашем случае:

R_3k = R₃, (1-41)

Е_кк – суммарная ЭДС к-ого контура.

Если ЭДС совпадет с направлением контурного тока, то она берётся положительной, и если не совпадает – отрицательной:

Е₁₁ = Е₂; Е₂₂ = 0; Е₃₃ = -Е₃. (1-42)

Далее нужно подставить численные значения сопротивлений резисторов, величины ЭДС и источника тока и решить системы уравнений для трёх неизвестных контуров токов I₁₁, I₂₂, I₃₃. Для решения проще всего воспользоваться методом Крамера.

Определим далее токи в ветвях через контурные токи. Если контурный ток совпадает с направлением тока ветви, то он берётся положительным, если не совпадает – отрицательным.

I₁ = I₃₃ – I₁₁; (1-43)

I₂ = I₁₁; (1-44)

I₃ = I₃₃ + I_кз; (1-45)

I₄ = I₁₁ – I₂₂; (1-46)

I₅ = - I₂₂; (1-47)

I₆ = I₃₃ – I₂₂; (1-48)

I₇ = - I₃₃. (1-49)

Из написанных токов выбивается из общего правила только ток I₃, при расчёте которого кроме контурного тока нужно учесть ещё и ток от источника тока I_кз, который в выражении тока I₃ входит со знаком «плюс», если совпадает с обозначенным направлением тока I₃, и со знаком «минус» - если не совпадают.