Частотные зависимости параллельного контура

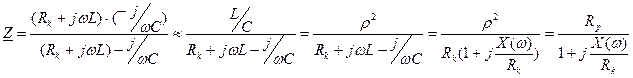
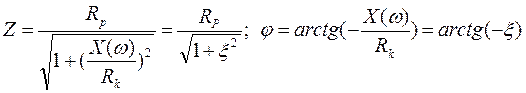
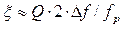
Если действует гармонический ток на контур, то при значении I_(m)=const действующее напряжение на контуре и амплитудное будет повторять зависимостьвеличины Z от w
.

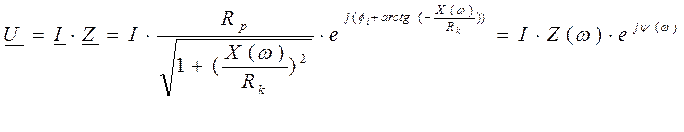
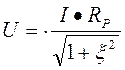
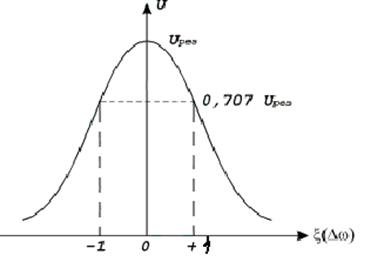
П=ω₂ – ω₁ (f₂ – f₁). Здесь полоса пропускания определяется по уровню 0,707 от максимального значения напряжения на контуре и обобщенная расстройка на границах равна +,- 1.

При резонансе (x=0) Х=0. Зависимость Х от x показана ниже . Параллельный колебательный контур на частоте ниже резонансной (x<0) ведет себя как некоторая индуктивность (Х>0), на частоте выше резонансной (x>0) – некоторая емкость (Х<0).

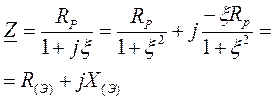
Здесь 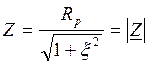, R_(Э)=Re(Z),

X_(Э)=Im(Z).

Схема исследования параллельного контура в EWB-5

Здесь показан источник напряжения (идеальный), его сопротивление Ri, вольтметр V. который надо настроить на измерение переменного напряжения и установить большое внутреннее сопротивление ( 1000 Мом) для большей точности. Так же здесь включены идеальные емкость С и индуктивность L и резистор, имитирующий сопротивление катушки (Rk).

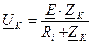
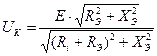
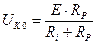
Расчетные графики частотных зависимостей напряжения