Под комплексной передаточной функцией понимают отношение комплексного изображения гармонической реакции ЛЭЦ к комплексному изображению гармонического воздействия на цепь.
Пусть воздействие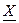 
, а реакция 
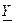; а комплексная передаточная функция 
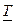. Тогда 
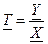. Если воздействие гармоническое и мы будем менять частоту, то получим комплексную частотную характеристику (КЧХ).
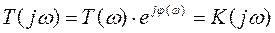
Сокращенно функцию T(jω) называют комплексным коэффициентом передачи. Модуль комплексного коэффициента T(ω) представляет собой амплитудно-частотную характеристику (АЧХ). Аргумент комплексного коэффициента передачи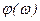 
- это фазово-частотная характеристика (ФЧХ).
АЧХ – это такая характеристика цепи, которая показывает, как изменяется в зависимости от частоты отношение амплитуды реакции (выходного сигнала) к амплитуде воздействия (входного сигнала) при гармоническом воздействии.
ФЧХ – это такая характеристика цепи, которая показывает, как изменяется сдвиг фаз выходного и входного сигнала в зависимости от частоты при гармоническом воздействии.
Это основные характеристики электрических цепей. Теоретически они рассчитываются с помощью расчетных методов на основе законов Ома и Кирхгофа в комплексной форме. Практически они измеряются с использованием приборов (вольтметров, фазометров, осциллографов).
В зависимости от вида реакции и воздействия различают четыре типа передаточных функций: по напряжению (напряжение / напряжение), по току (ток / ток), по сопротивлению (напряжение / ток), по проводимости (ток /напряжение ).
Для примера рассмотрим колебательный контур:
|
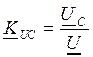
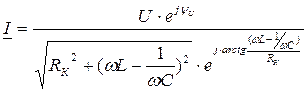
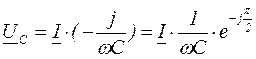
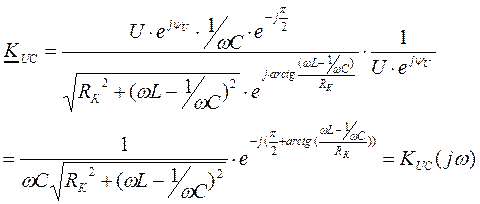
кривая пунктирная при Q<1,
при ω=ω0 К0=Q
С использованием расстройки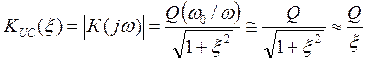 
Влияние внешнего сопротивления на избирательность контура
К внешним сопротивлениям относятся сопротивления источника сигнала и нагрузки. 
В идеале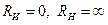 
и влияния нет. В противном случае они влияют на добротность контура, уменьшая ее и, соответственно, ухудшая избирательность. Эквивалентная добротность с учетом нагрузки может быть рассчитана
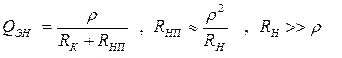. С учетом сопротивления источника
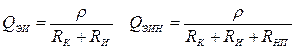- итоговая.
При той же частоте при меньшей добротности меньше коэффициент подавления помехи, так как обобщенная расстройка пропорциональна добротности. Нужно иметь источник с малым внутренним сопротивлением, катушку индуктивности с малыми потерями (толстым проводом или из дорогих материалов) и нагрузку с большим сопротивлением, тогда будет больше подавляться помеха при той же расстройке.
Параллельный колебательный контур (простой)
1. Идеализированный контур
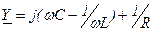- комплексная проводимость.
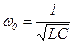- резонансная частота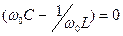 
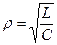- характеристическое сопротивление, сопротивление реактивного элемента на резонансной частоте,
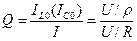, - усилительная способность контура где IL0, IC0 – токи при резонансной частоте; I – общий ток. 
, 
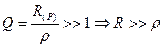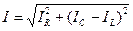. При резонансе емкостной ток компенсируется индуктивным и поэтому резонанс в параллельном контуре называется резонансом токов.
Полоса пропускания П определяется аналогично, как для последовательного контура по уровню половинной активной мощности. Коэффициент подавления помехи: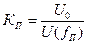 
Рассчитаем токи в ветвях идеального параллельного контура при резонансе. При резонансе (w=w0(Р)) токи в ветвях контура равны
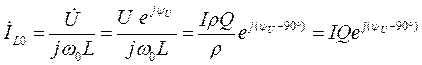
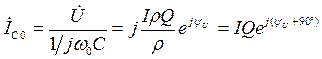
и в Q раз больше тока в общей ветви.
2. Реальный параллельный контур - это цепь из параллельно соединенных конденсатора и катушки индуктивности.
Схема замещения:
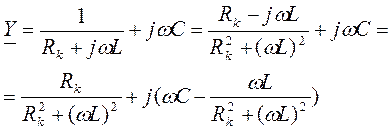
Условие резонанса: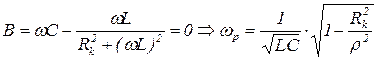 
, 
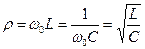
Условие приближения к идеальному контуру: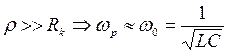 
Резонансное сопротивление:
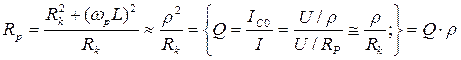
Векторная диаграмма:
Дата добавления: 2016-03-15; просмотров: 1382;