Как мы видим, в данном примере решение было бы легче при применении метода токов ветвей.

Пример 2 Здесь Е1- источник постоянной эдс, а j2 – источник переменного тока .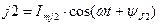

В данном случае мы можем использовать только метод наложения. Составим две схемы замещения, в первой из которых рассчитываются частичные токи от источника постоянной эдс. Поэтому в ней индуктивность заменена перемычкой, а емкость – разрывом. Во второй схеме рассчитываются частичные токи от источника переменного тока и здесь необходимо перевести все токи, напряжения и сопротивления в комплексную форму и записать законы Кирхгофа в комплексной форме.

I_1E1=E1/(R1+R2)=I_2E1=I_3E1. Тут надо составлять уравнения по МТВ в комплексной форме. Например, по 1 закону

I_1J2+ I_R2J2+ I_CJ2 –J₂=0, - I_CJ2 - I_R2J2+ I_3J2=0.

Можно использовать и общую проводимость относительно источника тока. 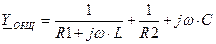, , 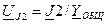, 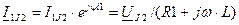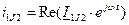. Аналогично остальные токи

В итоге получается, что i₁=I_1E1+i_{1 j2}, i_R2=I_R2E1 – i_R2j2, ic=i_cj2,

i₃=I_3E1 – i_3j2, i₂=j₂.

Теоремы об эквивалентных источниках или генераторах

(Теорема об автономном двухполюснике)

ЛАЭЦ – линейная активная электрическая цепь, содержит линейные