Методы повышения достоверности сигнатурного анализатора.

Наиболее полной характеристикой, описывающей свойства сигнатурного анализатора, является распределение вероятностей необнаружения ошибок в зависимости от их кратности. Поэтому одним из методов повышения достоверности может быть метод, основанный на увеличении старшей степени порождающего полинома m. Как показывают проведенные расчеты при m>8, вероятность необнаружения ошибки не зависит от кратности ошибки и близка к нулю, и дальнейшее возрастание m не приводит к сколь-нибудь заметному повышению достоверности сигнатурного анализатора. С другой стороны, увеличение значения m приводит к нежелательному расширению разрядности сигнатуры.

Имеются другие методы повышения достоверности сигнатурного анализатора, направленные количественное изменение 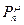.Достаточно хорошие результаты можно получить при использовании m сигнатурных анализаторов, описываемых одним и тем же полиномом φ(х). При этом каждый анализатор обрабатывает только определенное множество символов анализируемой последовательности. За счет этого ошибка, возникшая в исходной последовательности, представляется в виде ошибок различной конфигурации для каждого из m анализаторов. Таким образом, реальная ошибочная последовательность имеет вид множества искусственно образованных последовательностей, каждая из которых может содержать некоторое отличное от других множество ошибочных бит. Причем. Если хотя бы для одной последовательности ошибочные биты представляют собой обнаруживаемую конфигурацию анализатором, описываемым полиномом φ(х), то возникшая ошибка будет обнаруживаемой на основании всех m сигнатур. Простейшим примером разбиения исходной последовательности является использование символов кодов, определяющих номера элементов анализируемой последовательности. Пример подобного разбиения (m=4) для последовательности длиной l=2⁴ -1 приведен в таблице1.

Анализируемая последовательность представляется в виде четырех последовательностей, состоящих из нулевых символов и символов 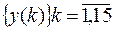. При этом для каждой из образованных последовательностей используется сигнатурный анализатор, описываемый полиномом φ(х), имеющим старшую степень, равную m=4. Каждый сигнатурный анализатор обнаруживает ошибки в зависимости от их кратности в соответствии с выражениями (10) и (11). Возникшая ошибка в исходной последовательности, предположим, состоящая из пяти неверных символов y(4), y(6), y(11), y(12) и y(13), отображается в виде искажения трех, четырех, двух и двух символов соответственно во вновь образованных четырех последовательностей. Следовательно, данная ошибка всегда будет обнаруживаемой, так как она представляется в виде двукратных ошибок для третьей и четвертой последовательностей, которые также обнаруживаемы. В общем случае любая ошибка, возникшая в исходной последовательности, отображается в виде некоторого множества ошибок меньшей кратности, мощность М₁ которого оценивается соотношением

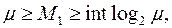
где μ-кратность возникшей ошибки. Отсюда следует, что любая трехкратная ошибка будет обнаруживаемой, так как она представляется по меньшей мере двумя ошибками кратности 2 или 1.Аналогичным образом можно доказать возможность обнаружения всех ошибок кратности 4, 5 и т. д. Причем максимальная кратность μ обнаруживаемых ошибок в общем случае зависит от величины m.

Таблица 1.

№ элемента последовательности	Анализируемая последовательность	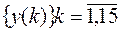Искусственно образованная последовательность
	y1				y1
	y2			y2
	y3			y3	y3
	y4		y4
	y5		y5		y5
	y6		y6	y6
	y7		y7	y7	y7
	y8	y8
	y9	y9			y9
	y10	y10		y10
	y11	y11		y11	y11
	y12	y12	y12
	y13	y13	y13		y13
	y14	y14	y14	y14
	y15	y15	y15	y15	y15
Кратность ошибки	μ =5	μ=2	μ =4	μ =2	μ =2