Оценка достоверности сигнатурного анализатора.

Полнота необнаружения неисправностей цифровой схемы в первую очередь зависит от качества тестовых воздействий. Если определённая неисправность не проявляется в виде искажения их символов, то она не может быть обнаружена в результате применения сигнатурного анализа, который является не более чем эффективным методом сжатия потока данных. Поэтому если этот поток не несёт информации о неисправности, то она и не появится после его сжатия.

Таким образом, под достоверностью сигнатурного анализа будем понимать его эффективность обнаружения ошибки в потоке сжимаемых данных. Для оценки этой характеристики сигнатурного анализа могут использоваться разные подходы и методы. Наиболее широко применяемым является вероятностный подход, сущность которого заключается в определении вероятности P_n необнаружения ошибок в анализируемой последовательности данных. Причём в рассматриваемом случае оценивается вероятность, зависящая только от метода сжатия, и не учитываются другие факторы.

Величина P_n рассчитывается для общего случая, приближённо соответствующего реальным примерам. Предполагается, что эталонная последовательность данных может равновероятно принимать разное значение, а любая конфигурация ошибочных бит может быть равновероятным событием. Далее, используя алгоритм деления полиномов как математический аппарат формирования сигнатуры, показываем, что для 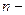разрядного делимого вычисляются n-m разрядное частное и m-разрядный остаток (сигнатура). При этом соответствие реальной последовательности, состоящей из n бит, эталонной оценивается только по равенству их m разрядных сигнатур. Для 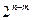различных частных будет формироваться одинаковая сигнатура. Это свидетельствует о том, что 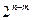-1 ошибочных n-разрядных последовательностей будут считаться соответствующими одной ¾ эталонной. Учитывая равновероятность ошибочных последовательностей данных, можно заключить, что 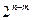-1 ошибочных последовательностей, инициирующих эталонную сигнатуру, необнаруживаемы. Таким образом, вероятность P_n необнаружения ошибок в анализируемой последовательности данных будет вычисляться как отношение:

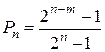, (2.6)

где 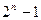равняется общему числу ошибочных последовательностей.

Выражение (2.6) для условия 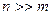преобразуется к более простому виду

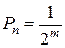, (2.7)

которое может служить основным аргументом для обоснования высокой эффективности сигнатурного анализа.

В сигнатурных анализаторах, выпускаемых различными фирмами, обычно .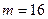

В качестве более точной меры оценки достоинств сигнатурного анализатора рассмотрим распределение вероятности необнаружения ошибки в зависимости от её кратности 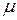, т.е. определим значения 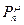, где .

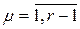Можно показать, что количество 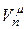необнаруживаемых ошибок определяется следующим образом:

; ; ,

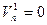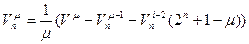а количество возможных ошибок из 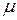бит определяется как .

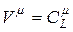И тогда выражение для вероятности необнаружения ошибки принимает вид:

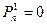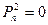, , (2.8)

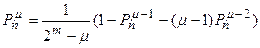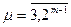, . (2.9)

Для сигнатурного анализатора, построенного на основе полинома 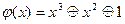, вероятности необнаружения ошибок различных кратностей выглядит так:

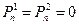
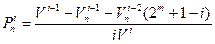(2.10)

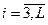
где Vⁱ=C_Lⁱ. Для i=3, 4, 5, 6, 7 на основе (2.8) получим

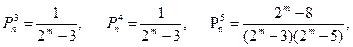
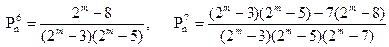
Анализируя полученные значения Р_nⁱ, а также выражение (3.1.8), можно заметить, что для достаточно больших величин m Р_nⁱ≈1/2^m. Таким образом, ошибки кратности i, i Є {3, 4, 5, ..., L—1}, возникающие в последовательности данных длиной L, обнаруживаются сигнатурным анализатором с одинаковой вероятностью, равной 1—1/2^m, которая при m>8 практически равна единице 1. Важным следствием выражения (3.1.8) является то, что вероятность необнаружения ошибок не зависит от вида примитивного и неприводимого полинома φ(x), a определяется только величиной m=degφ(x).