Потенциал электрического поля
Теоретическая часть:
| № | Вопрос | Варианты ответа |
| Криволинейный интеграл по произвольному замкнутому контуру от напряженности электростатического поля равен 0. Это теорема… | 1. о циркуляции 2. о смещении 3. о замкнутости 4. о напряженности | |
Если циркуляция напряженности электростатического поля равна 0, то…
1. 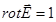 2.
2. 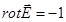 3.
3. 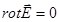 4.
4. 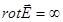
| 1. 3 2. 1 3. 2 4. 4 | |
| Единица разности потенциалов: | 1. 1 Вольт 2. 1 фарад 3. 1 Джоуль 4. 1 Кулон | |
Если в каждой точке области пространства V задано некоторое число 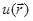 , то говорят, что в этой области пространства определено... , то говорят, что в этой области пространства определено...
| 1. скалярное поле 2. векторное поле 3. силовое поле 4. внешнее поле | |
| Градиентом скалярной функции u(x,y,z) называется… | 1. вектор, направленный в сторону максимального возрастания этой функции в данной точке пространства, а его длина равна производной функции в том же направлении. 2. скаляр, направленный в сторону максимального возрастания этой функции в данной точке пространства, а его длина равна производной функции в том же направлении. 3. вектор, направленный в сторону минимального возрастания этой функции в данной точке пространства, а его длина равна производной функции в том же направлении. 4. скаляр, направленный в сторону минимального возрастания этой функции в данной точке пространства, а его длина равна производной функции в том же направлении. |
Формулы:
| № | Вопрос | Варианты ответа |
Криволинейный интеграл по произвольному замкнутому контуру от напряженности электростатического поля:
1. 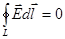 2.
2. 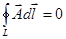 3.
3. 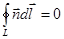 4.
4. 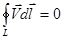
| 1. 1 2. 2 3. 3 4. 4 | |
Формула Стокса:
1. 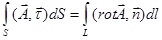 2.
2. 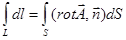 3.
3. 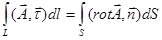 4.
4. 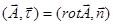
| 1. 3 2. 1 3. 2 4. 4 | |
Разность потенциалов:
1. 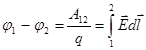 2.
2. 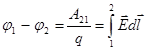 3.
3. 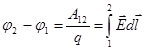 4.
4. 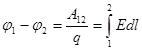
| 1. 1 2. 2 3. 3 4. 4 | |
Потенциал точечного заряда:
1. 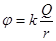 2.
2. 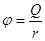 3.
3. 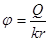 4.
4. 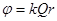
| 1. 1 2. 2 3. 3 4. 4 | |
Лапласиан скалярного поля:
1. 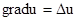 2.
2. 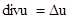 3.
3. 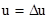 4.
4. 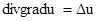
| 1. 4 2. 1 3. 2 4. 3 | |
Уравнение Пуассона:
1. 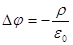 2.
2. 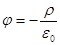 3.
3. 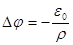 4.
4. 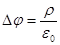
| 1. 1 2. 2 3. 3 4. 4 |
Дата добавления: 2016-03-10; просмотров: 749;
