Напряженность электрического поля
Теоритическая часть:
| № | Вопрос | Варианты ответа |
| Напряженность электрического поля – это… | 1. физическая величина, являющаяся отношением силы, действующей со стороны электрического поля на пробный заряд, к величине этого заряда 2. физическая величина, являющаяся отношением величины заряда к силе, действующей со стороны электрического поля на пробный заряд 3. физическая величина, являющаяся произведением силы, действующей со стороны электрического поля на пробный заряд, к величине этого заряда 4. физическая величина, являющаяся произведением величины заряда к силе, действующей со стороны электрического поля на пробный заряд | |
| Напряженность – это… | 1. векторная функция зарядов-источников электрического поля 2. физическая величина, являющаяся источником поля, посредством которого осуществляется взаимодействие заряженных частиц 3. векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы F, действующей на неподвижный точечный заряд 4. векторная физическая величина, являющаяся источником поля, посредством которого осуществляется взаимодействие заряженных частиц | |
| Единица SI напряженности электрического поля - … | 1. В/м 2. В 3. м 4. Кл | |
| Напряженность поля в точке пространства равна… | 1. сумме напряженностей полей, создаваемых отдельными точечными зарядами. 2. разности напряженностей полей, создаваемых отдельными точечными зарядами. 3. произведению напряженностей полей, создаваемых отдельными точечными зарядами. 4. частному напряженностей полей, создаваемых отдельными точечными зарядами. | |
| Физическое поле – это… | 1. особая форма материи, физическая система с бесконечно большим числом степеней свободы, которая осуществляет взаимодействие между частицами, но может существовать и без частиц. 2. особая форма материи, физическая система с бесконечно малым числом степеней свободы, которая осуществляет взаимодействие между частицами, но может существовать и без частиц. 3. особая форма материи, физическая система с бесконечно большим числом степеней свободы, которая запрещает взаимодействие между частицами, но может существовать и без частиц. 4. особая форма материи, физическая система с бесконечно большим числом степеней свободы, которая осуществляет взаимодействие между частицами, но не может существовать без частиц. |
Формулы:
| № | Вопрос | Варианты ответа |
Напряженность электрического поля:
1. 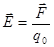 2.
2. 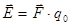 3.
3. 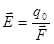 4.
4. 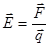
| 1. 1 2. 2 3. 3 4. 4 | |
Напряженность определяется по следующей формуле:
1. 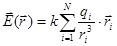 2.
2. 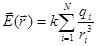 3.
3. 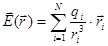 4.
4. 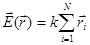
| 1. 1 2. 2 3. 3 4. 4 | |
Напряженность поля в точке пространства равна:
1. 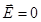 2.
2. 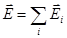 3.
3. 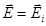 4.
4. 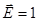
| 1. 2 2. 1 3. 3 4. 4 |
Практическая часть:
| № | Вопрос | Варианты ответа |
«На заряд q = 2⋅10−7 Кл, находящийся в некоторой точке электрического поля, действует сила F = 1,5⋅10−2 Н. Какова напряжённость поля в этой точке?» [4, стр.84]
1. 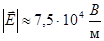 2.
2. 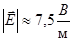 3.
3. 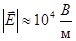 4.
4. 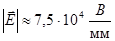
| 1. 1 2. 2 3. 3 4. 4 | |
Решение:
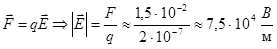 Ответ:
Ответ: 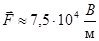
| ||
«Оценить заряд земного шара, если напряжённость электрического поля у поверхности составляет Е ≈ 100 В/м?» [3, стр.85]
1. 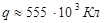 2.
2. 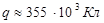 3.
3. 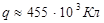 4.
4. 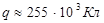
| 1. 3 2. 1 3. 2 4. 4 | |
Решение:
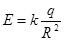 ; ;
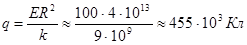 Ответ:
Ответ: 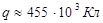
| ||
| «В точке A напряжённость поля, создаваемого точечным положительным зарядом Е1 = 36 В/м, а в точке В Е2 = 9 В/м. Определить напряжённость поля в точке С, находящейся в середине отрезка АВ» [4, стр.86]. 1. E3=166 В/м 2. E3=16 В/м 3. E3=167 В/м 4. E3=168 В/м | 1. 2 2. 1 3. 3 4. 4 | |
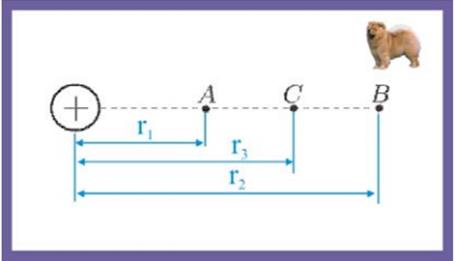 1. Напряженность поля в заданных точках:
1. Напряженность поля в заданных точках: 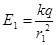 ; ; 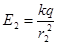 ; ;
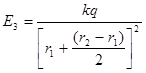 .
2. Расстояния от точечного заряда до заданных точек: .
2. Расстояния от точечного заряда до заданных точек: 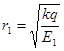 ; ; 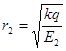 ; ;
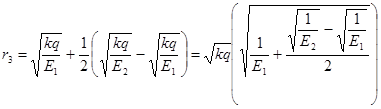 ; ;
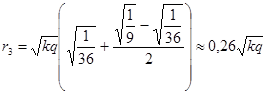 ; ;
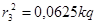 . .
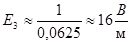 .
Ответ: .
Ответ: 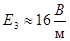
| ||
«В двух точках, находящихся на расстоянии r1 = 1 м друг от друга в воздухе помещены заряды q1 = 8⋅10−6 Кл и q2 = 7,2⋅10−6 Кл. Определить напряжённость поля, созданного этими зарядами в точке, лежащей на расстоянии r2 = 0,4 м от первого заряда, на прямой, соединяющей заряды» [4, стр.87].
1. 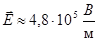 2.
2. 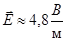 3.
3. 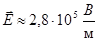 4.
4. 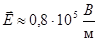
| 1. 1 2. 2 3. 3 4. 4 | |
Решение:
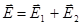 ; ; 
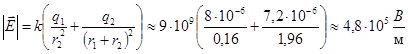 Ответ:
Ответ: 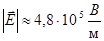 . .
|
Теорема Гаусса
Теоретическая часть:
| № | Вопрос | Варианты ответа |
| Совокупность неподвижных частиц, взаимодействующих между собой с силой, обратно пропорциональной квадрату расстояния не может образовывать устойчивой равновесной системы. Это теорема… | 1. Ирншоу 2. Гаусса 3. Лагранжа 4. Гюйгенса | |
Теорема Гаусса в диэлектриках (в интегральной форме):
1. 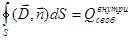 2.
2. 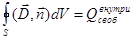 3.
3. 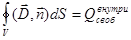 4.
4. 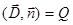
| 1. 1 2. 2 3. 3 4. 4 | |
Теорема Гаусса в диэлектриках (в дифференциальной форме):
1. 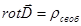 2.
2. 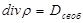 3.
3. 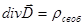 4.
4. 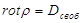
| 1. 3 2. 1 3. 2 4. 4 |
Формулы:
| № | Вопрос | Варианты ответа |
Потоком векторного поля через поверхность S называется поверхностный интеграл:
1. 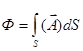 2.
2. 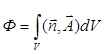 3.
3. 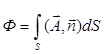 4.
4. 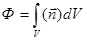
| 1. 3 2. 1 3. 2 4. 4 | |
Если поверхность S является замкнутой, то поток вектора 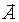 через такую поверхность обозначается:
1. через такую поверхность обозначается:
1. 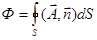 2.
2. 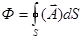 3.
3. 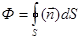 4.
4. 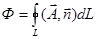
| 1. 1 2. 2 3. 3 4. 4 | |
Теорема Остроградского-Гаусса (Теорема Гаусса) в физике:
1. 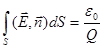 2.
2. 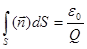 3.
3. 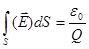 4.
4. 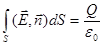
| 1. 4 2. 1 3. 2 4. 3 |
Практическая часть:
| № | Вопрос | Варианты ответа | |
Точечный заряд +q находится в центре сферической поверхности. Если добавить заряд +q за пределами сферы, то поток вектора напряженности электростатического поля 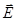 через поверхность сферы… через поверхность сферы…
| 1. не изменится 2. увеличится 3. уменьшится 4. недостаточно данных для ответа | ||
Пояснение:По теореме Гаусса поток вектора напряженности через замкнутую поверхность определяется зарядом внутри этой поверхности 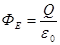 – поток вектора напряжённости электрического поля – поток вектора напряжённости электрического поля 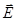 . .
| |||
Точечный заряд +q находится в центре сферической поверхности. Если увеличить радиус сферической поверхности, то поток вектора напряженности электростатического поля 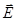 через поверхность сферы… через поверхность сферы…
| 1. не изменится 2. увеличится 3. уменьшится 4. недостаточно данных для ответа | ||
Пояснение:По теореме Гаусса поток вектора напряженности через замкнутую поверхность определяется зарядом внутри этой поверхности 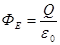 – поток вектора напряжённости электрического поля – поток вектора напряжённости электрического поля 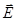 . .
| |||
Точечный заряд +q находится в центре сферической поверхности. Если уменьшить радиус сферической поверхности, то поток вектора напряженности электростатического поля 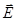 через поверхность сферы… через поверхность сферы…
| 1. не изменится 2. увеличится 3. уменьшится 4. недостаточно данных для ответа | ||
Пояснение:По теореме Гаусса поток вектора напряженности через замкнутую поверхность определяется зарядом внутри этой поверхности 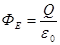 – поток вектора напряжённости электрического поля – поток вектора напряжённости электрического поля 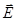 . .
| |||
Точечный заряд +q находится в центре сферической поверхности. Если заряд сместить из центра сферы, оставляя его внутри нее, то поток вектора напряженности электростатического поля 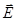 через поверхность сферы… через поверхность сферы…
| 1. не изменится 2. увеличится 3. уменьшится 4. недостаточно данных для ответа | ||
Пояснение:По теореме Гаусса поток вектора напряженности через замкнутую поверхность определяется зарядом внутри этой поверхности 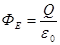 – поток вектора напряжённости электрического поля – поток вектора напряжённости электрического поля 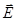 . .
| |||
Точечный заряд +q находится в центре сферической поверхности. Если добавить заряд +q внутрь сферы, то поток вектора напряженности электростатического поля 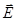 через поверхность сферы… через поверхность сферы…
| 1. увеличится 2. не изменится 3. уменьшится 4. недостаточно данных для ответа | ||
Пояснение: По теореме Гаусса: 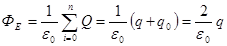 . .
| |||
Точечный заряд +q находится в центре сферической поверхности. Если добавить заряд –q внутрь сферы, то поток вектора напряженности электростатического поля 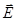 через поверхность сферы… через поверхность сферы…
| 1. уменьшится 2. увеличится 3. не изменится 4. недостаточно данных для ответа | ||
Пояснение: По теореме Гаусса: 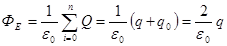 . .
| |||
Поток вектора напряженности электростатического поля через замкнутую поверхность S равен…
1. 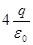 2.
2. 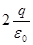 3.
3. 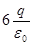 4.
4. 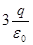
| 1. 2 2. 1 3. 3 4. 4 | ||
Пояснение: По теореме Гаусса: 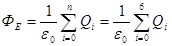
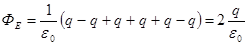 . .
| |||
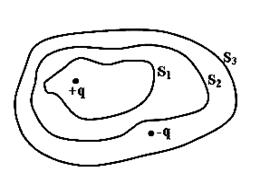
Дана система точечных зарядов в вакууме и замкнутые поверхности 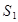 , ,  и и 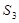 . Поток вектора напряженности электростатического поля отличен от нуля через…
1. поверхности . Поток вектора напряженности электростатического поля отличен от нуля через…
1. поверхности  и и  2. поверхность
2. поверхность  3. поверхность
3. поверхность  4. поверхность
4. поверхность 
| 1. 1 2. 2 3. 3 4. 4 | ||
Пояснение: Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 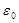 . .
| |||
Дана система точечных зарядов в вакууме и замкнутые поверхности 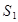 , ,  и и 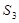 . Поток вектора напряженности электростатического поля равен нулю через…
1. поверхность . Поток вектора напряженности электростатического поля равен нулю через…
1. поверхность 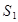 2. поверхность
2. поверхность  3. поверхности
3. поверхности  и и  4. поверхность
4. поверхность 
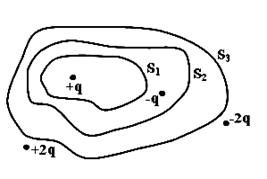
| 1. 3 2. 1 3. 2 4. 4 | ||
Пояснение: Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 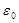 . .
| |||
Дана система точечных зарядов в вакууме и замкнутые поверхности 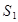 , ,  и и 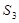 . Поток вектора напряженности электростатического поля отличен от нуля через…
1. поверхность . Поток вектора напряженности электростатического поля отличен от нуля через…
1. поверхность 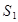 2. поверхности
2. поверхности  и и 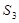 3. поверхность
3. поверхность  4. поверхность
4. поверхность 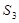
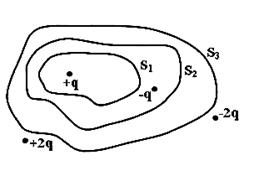
| 1. 1 2. 2 3. 3 4. 4 | ||
Пояснение: Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 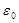 . .
| |||
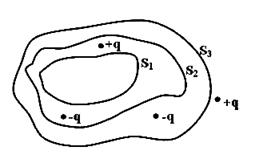
Дана система точечных зарядов в вакууме и замкнутые поверхности 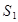 , ,  и и 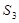 . Поток вектора напряженности электростатического поля равен нулю через…
1. поверхности . Поток вектора напряженности электростатического поля равен нулю через…
1. поверхности  и и 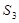 2. поверхность
2. поверхность  3. поверхность
3. поверхность 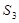 4. поверхность
4. поверхность 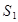 и и 
| 1. 4 2. 1 3. 2 4. 3 | ||
Пояснение: Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 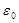 . .
| |||
Дана система точечных зарядов в вакууме и замкнутые поверхности 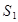 , ,  и и 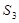 . Поток вектора напряженности электростатического поля отличен от нуля через…
1. поверхность . Поток вектора напряженности электростатического поля отличен от нуля через…
1. поверхность  2. поверхность
2. поверхность  и и  3. поверхности
3. поверхности  и и  4. поверхность
4. поверхность 
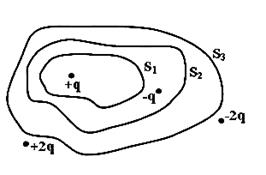
| 1. 1 2. 2 3. 3 4. 4 | ||
Пояснение: Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 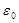 . .
| |||
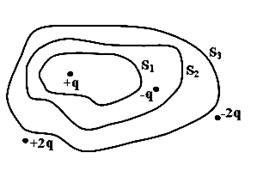
Дана система точечных зарядов в вакууме и замкнутые поверхности 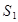 , ,  и и 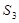 . Поток вектора напряженности электростатического поля равен нулю через поверхности...
1. поверхность . Поток вектора напряженности электростатического поля равен нулю через поверхности...
1. поверхность 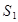 и и  2. поверхности
2. поверхности  и и  3. поверхности
3. поверхности  4. поверхность
4. поверхность 
| 1. 2 2. 1 3. 3 4. 4 | ||
Пояснение: Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 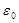 . .
| |||
Дана система точечных зарядов в вакууме и замкнутые поверхности 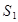 , ,  и и 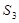 . Если поток вектора напряженности электростатического поля через замкнутую поверхность . Если поток вектора напряженности электростатического поля через замкнутую поверхность 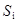 обозначим как обозначим как 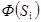 , то верными утверждениями являются...
1. , то верными утверждениями являются...
1. 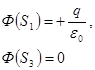 2.
2. 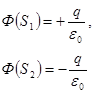 3.
3. 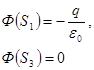 4.
4. 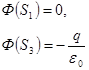
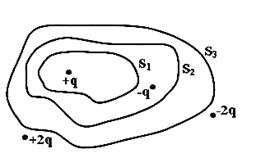
| 1. 1 2. 2 3. 3 4. 4 | ||
Пояснение:По теореме Гаусса:
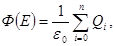
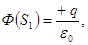
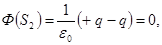
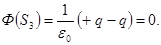
| |||
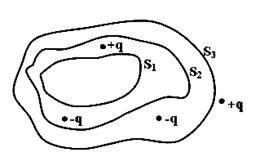
Дана система точечных зарядов в вакууме и замкнутые поверхности 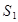 , ,  и и 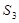 . Поток вектора напряженности электростатического поля равен нулю через поверхности ...
1. поверхности . Поток вектора напряженности электростатического поля равен нулю через поверхности ...
1. поверхности 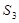 и и  2. поверхности
2. поверхности  3. поверхность
3. поверхность 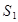 и и  4. поверхность
4. поверхность 
| 1. 3 2. 1 3. 2 4. 4 | ||
Пояснение: Теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на 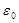 . .
| |||
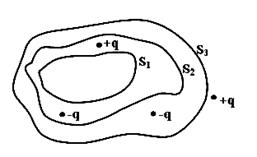
Дана система точечных зарядов в вакууме и замкнутые поверхности 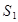 , ,  и и 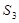 . Если поток вектора напряженности электростатического поля через замкнутую поверхность . Если поток вектора напряженности электростатического поля через замкнутую поверхность 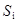 обозначим как обозначим как 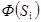 , то верными утверждениями являются…
1. , то верными утверждениями являются…
1. 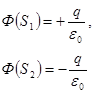 2.
2. 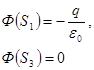 3.
3. 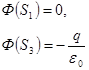 4.
4. 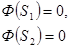
| 1. 4 2. 1 3. 2 4. 3 | ||
Пояснение:По теореме Гаусса:
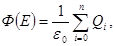
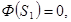
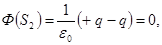
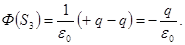
| |||
Дата добавления: 2016-03-10; просмотров: 2069;
